МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение уравнений и систем уравнений

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение уравнений и систем уравнений

Цель работы: 

- применить умения по владению стандартными приемами решения уравнений и систем.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Определение 1. Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют равносильными, если множества их корней совпадают.

Определение 2. Если каждый корень уравнения f(x)=g(x) является в тоже время корнем уравнения p(x)=h(x), то уравнение второе называют следствием уравнения.

Решение любого уравнения проходит в три этапа:

1: − технический. На этом этапе проводятся преобразования, ведущие к нахождению корня.

2: − анализ решения. Анализируя проведённые преобразования, отвечают на вопрос об отборе корней и их количестве.

3: − проверка.

Иногда при решении уравнений происходит потеря корней.

Есть 2 причины:

1)      деление обеих частей уравнения на одно и тоже число;

2)      сужение ОДЗ в процессе решение уравнения.

Рассмотрим общие методы решения уравнений.

            1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x)=g(x).

Этот метод применяем:

- при решении показательных уравнений, когда переходим от уравнения  к уравнению f(x)=g(x);

- при решении логарифмических уравнений, когда переходили от уравнения log_a f(x) = log_a g(x) к уравнению f(x)=g(x);

- при решении иррациональных уравнений, когда переходили от уравнения    к уравнению f(x)=g(x).

Этот метод можно применять только в том случае, когда y=h(x) − монотонная функция, которая каждое своё значение принимает по одному разу.

            2. Метод разложения на множители.

Суть этого метода заключается в следующем: уравнение f(x)g(x)h(x) = 0 можно заменить совокупностью уравнений f(x)=0;  g(x)=0;  h(x)=0.

Решив уравнения этой совокупности, нужно взять те корни, которые принадлежат области определения, а остальные отбросите как посторонние.

            3.Метод введения новой переменной.

Если уравнение f(x)=0 удалось преобразовать к виду p(g(x))=0, то нужно ввести новую переменную u=g(x), решить уравнение p(u)=0,

=> g(x)=u₁; g(x)=u₂; ...; g(x)=u_n , где u₁, u₂ , ... , u_n −корни уравнения p(u)=0.

            4. Функционально - графический метод.

Чтобы решить графически уравнение f(x)=g(x), нужно построить графики функций y=f(x) b y=g(x) и найти точки их пересечения. Корнями уравнения служат абсциссы этих точек.

Определение 1. Если поставлена задача - найти такие пары значений (x;y), которые одновременно удовлетворяют уравнению p(x;y)=0  и уравнению g(x;y)=0, то говорят, что данные уравнения образуют систему уравнений.

Пару значений (x;y), которая одновременно является решением первого и второго уравнения системы, называют решением системы.

Определение 2. Две системы называются равносильными, если они имеют одни и те же решения или решений нет.

Системы можно решить графически, методом алгебраического сложения, методом подстановки.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

Решить уравнения x³-7x+6=0.

Решение:        x³-x-6x+6=0.

                  x(x²-1)-6(x-1)=0.

          x(x-1)(x+1)-6(x-1)=0.

                 x(x-1)(x²+x-6)=0.

            x-1=0       x²+x-6=0.

               x=1              x₂ =2.

                                   x₃=-3.

    Ответ: 1;2;-3.

Пример 2.

 Решите уравнение:  cos 2x-5sin x-3=0.

Решение:  u=sin x ,

cos 2x =cos² x - sin² x =  1- sin²x - sin²x = 1-2u²

1-2u² - 5u-3=0.                   sin x =

  -2u² - 5u-2=0.               .

u₁ = ; u₂=-2.                  sin x =-2,

      Ответ: .

Пример 3.

 Решить уравнение

Решение. Графики функций y= и y=|x-2|  постройте в одной координатной плоскости.

Они пересекаются в точках А(1;1) и В(4;2)

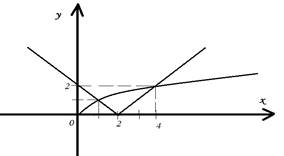
Значит, уравнение имеет два корня x₁=1 x₂=4. Ответ : 1;4.

Пример 4.

Решить систему уравнений

Решение.

Решим способом подстановки:

;   ;   ;                    

 Ответ: (-7;3)(1;-1)

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Перечислите методы решений уравнений.

2.    Что значит решить систему уравнений?

3.    Объясните алгоритм решения систем уравнений способом подстановки.

4.    Перечислите методы решения квадратного уравнения.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.