МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Обратные тригонометрические функции».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Обратные тригонометрические функции».

Цель работы: 

- применить  умения использования определений обратных тригонометрических функций для решения задач по теме.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:                 

I Вариант                                                                           II Вариант

1. Вычислите

a) arcsin1 – arctg 0;                                                        a) arcos 0 – arctg 1;

б) arcos  + arctg;                                            б) ;

в) ctg .                                                    в) .

2. Сравните числа

                                                                .

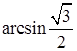
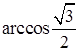3. Определите, имеет ли смысл выражение

arcsin(x-1) при x=;                                                     arcos(x+1) при x= ;

x=0,9; x= sin .                                                         x= cos.

Ответ объясните.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Обратные тригонометрические функции:

arcsin a, arcos a, arctg a, arcctg a.

1. Арксинусом числа а Є [-1; 1] называется такое число α Є , синус которого равен a :

arcsin a = , если sin α = a и .

Например, , так как  и ;

, так как  .

2. Арккосинусом числа a Є [-1 ; 1] называется такое число α Є [0;π],

косинус которого равен α :

arcos a=α , если cosα=a и 0

Например , arccos и 0;

arcos (-так как   и 0

3. Арктангенсом числа a Є R называется такое число α Є тангенс которого равен а: , arctg a = α, если tgα = a и  .

Например, arctg 1 =  , так как  ;

arctg ()=, так как .

4.Арккотангенсом числа а Є R называется такое число α Є (0 ; π), котангенс которого равен а :

arcctg a = α, если ctgα = a, 0 < α <π.

Например, arcctg, так как ctg ;

arcctg( -1 ) = , так как ctg .

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

Сравнить числа:

     >   

                   >          

                >          

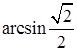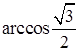
Пример 2:

Определить, имеет ли смысл выражение.

arcsin (x-1) при x =

- 1x -11

0 ,  Є  [ 0 ;  2 ]

Ответ: при x= выражение arcsin (x-1) не имеет смысла.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Сформулируйте определение арксинуса числа а.

2. Сформулируйте определение арккосинуса числа а.

3. Сформулируйте определение арктангенса числа а.

4. Сформулируйте определение арккотангенса числа а.

5. Допишите формулы :

arccos(-a)=

arcsin(-a)=

arctg(-a)=

arcctg(-a)=

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.