МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Перпендикуляр и наклонная к плоскости».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Перпендикуляр и наклонная к плоскости».

Цель работы: 

- применить  умения и навыки применения изученных теоретических фактов в ходе решения задач

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1

№ 1. АВСD – квадрат, ВМ            (АВС). Найдите отрезок DM, если см, а ВМ = 5 см.

№ 2. КО – перпендикуляр к плоскости α, КМ и КР – наклонные к плоскости α, ОМ и ОР – проекции наклонных, причем сумма их длин равна 15 см. Найдите расстояние от точки К до плоскости α, если КМ = 15 см и КР =  см.

 № 3. Треугольник АВС – прямоугольный, С = 90⁰ , АС = 8 см, ВС = 6 см. Отрезок СD – перпендикуляр к плоскости АВС. Найдите СD, если расстояние от точки D  до стороны АВ равно 5 см.

№ 4. Треугольник МКN равносторонний со стороной, равной 18 см. Точка С удалена от вершин треугольника МКN на 12 см. Найдите расстояние от точки С до плоскости МКN.

№ 5. АВСD – квадрат. Точка М удалена от сторон квадрата на  см. Найдите периметр квадрата, если точка М удалена от плоскости АВС на  см.

№ 6. АВСDA₁В₁С₁D₁ – куб. Найдите расстояние между прямыми АВ₁ и ВС, если ребро куба равно см.

Вариант 2       

№ 1. СDEK – квадрат со стороной, равной 2 см. ВD  (СDЕ). Найдите расстояние от точки В до плоскости CDE, если см.

№ 2. ВО – перпендикуляр к плоскости α, ВА и ВС – наклонные, ОА и ОС – их проекции на плоскость α, причем сумма их длин равна 24 см. Найдите расстояние от точки В до плоскости α, если АВ = см и ВС = 12 см.

№ 3. Треугольник АВС – прямоугольный, А = 60⁰, С = 90⁰ . СН – высота треугольника АВС, причем СН = 8 см. Отрезок ВК перпендикуляр к плоскости треугольника АВС. Найдите отрезок ВК, если расстояние от точки К  до стороны АС равно 20 см.

№ 4. Треугольник АСD -  равносторонний. Точка S удалена от вершин треугольника ACD на 6 см, а от плоскости треугольника АСD на 3 см. Найдите сторону треугольника АСD.

№ 5. АВСD – квадрат с периметром, равным 16 см. Точка Е удалена от всех сторон квадрата на 4 см. Найдите расстояние точки Е от плоскости АВС.

№ 6. АВСDA₁В₁С₁D₁ – куб, ребро которого равно см. Найдите расстояние между прямыми СС₁ и DВ₁.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Перпендикуляр и наклонная
Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

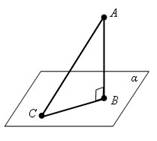
AB – перпендикуляр к плоскости α.
AC – наклонная, CB – проекция.
С – основание наклонной, B - основание перпендикуляра.

Теорема о трех перпендикулярах

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной.

Обратная теореме о трех перпендикулярах

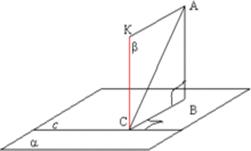
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

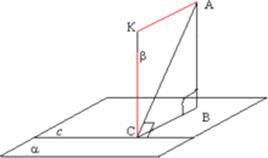
При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

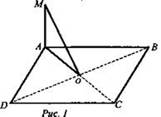
Дано: ABCD квадрат; AM - прямая; АМ ⊥ (ABCD); АС ∩ BD = О (рис. 1).

Доказать: a) BD ⊥ (АМО); б) МО ⊥ BD.

Доказательство:

1) Так как МА ⊥ (ABCD), то МА ⊥ BD (по определению прямой, перпендикулярной плоскости). BD ⊥ AC (по свойству диагоналей квадрата). МА ⊂ (МАО) и АС ⊂ (МАО), МА ∩ АС = А. Следовательно, BD ⊥  (MAO) (по признаку перпендикулярности прямой и плоскости).

2) Так как BD ⊥ (МАО), то BD ⊥ МО, МО ⊂ (МАО) (по определению прямой, перпендикулярной плоскости).

Пример 2.

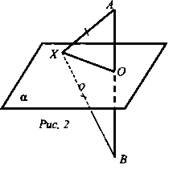
Дано: АВ - отрезок; α; АВ ⊥ α; О - середина АВ, О ∈ α; ХА = ХВ. (рис. 2).

Доказать: X ∈ α.

 Доказательство:

1) Если X ∈ АВ, то Х = О, и поэтому X ∈ а.

2) Если X ∉ АВ, то ХО - медиана ΔАХВ. ΔАХВ - равнобедренный (по определению), значит, ХО - высота (по свойству медианы равнобедренного треугольника), то есть ХО ⊥ АВ. Таким образом, О ∈ ХО, О ∈ АВ и ХО ⊥ АВ, следовательно, ХО ⊂ а (по задаче № 134) и X ∈ а.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Дайте определение перпендикуляра, основания перпендикуляра, расстояния от точки до плоскости, наклонной, основания наклонной, проекции наклонной?

3. Сформулируйте теорему о трех перпендикулярах.

4.Сформулируйте  обратную теорему о трех перпендикулярах

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.

Скачано с www.znanio.ru