МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Площадь поверхности».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Площадь поверхности».

Цель работы: 

- применить умения по владению основными понятиями пространственных геометрических фигурах, их основных свойствах − владение;

- применить умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант

1) Основание прямой призмы - прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань - квадрат.

2) Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45°.

а)    Найдите высоту пирамиды.

б)    Найдите площадь боковой поверхности пирамиды.

3) Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.

II Вариант

1) Основание прямой призмы - прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань - квадрат.

2) Высота правильной четырехугольной пирамиды равна √6 см, а боковое ребро наклонено к плоскости основания под углом 60°.

а)    Найдите боковое ребро пирамиды.

б)    Найдите площадь боковой поверхности пирамиды.

3) Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середины ребер DA и АВ параллельно ребру ВС, и найдите площадь этого сечения.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Площадь поверхности многогранника находится как сумма площадей всех его граней.

   Площадь поверхности призмы равна

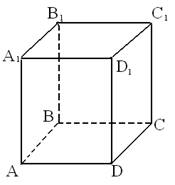
                    Площадь боковой поверхности прямой призмы равна произведению периметра       основания на   высоту.

                     Площадь поверхности пирамиды:   

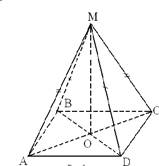
При выполнении практической работы рассмотрите следующие задачи:

Задача 1.

1.      Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.

2.      Решение:

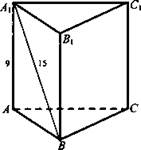
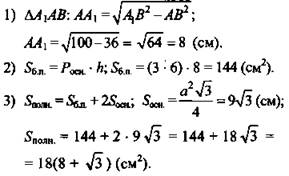
Ответ: 

Задача 2.

Основание прямой призмы - ромб со стороной 5 см и тупым углом 120°. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.

1) ∠ABC= 120°; ∠BAD = 60°; ΔABD - равносторонний; BD = 5 см.

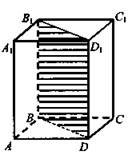
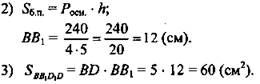
Ответ: Scеч. = 60 см2 .

Основание пирамиды - прямоугольник со сторонами 6 и 8 см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.

Дано: SABCD - пирамида; ABCD — прямоугольник; SO = 12 (см); АВ = 6 (см); ВС = 8 (см).

Найти: SD.

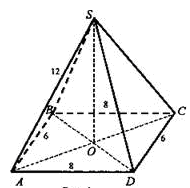
Решение: Пусть SABCD - данная пирамида, SO ⊥ ABCD. ΔABD - прямоугольный. По теореме Пифагора получим:  ВО = OD = 5 (см); ΔSOD – прямоугольный треугольник.  Ответ: SD = 13 см.

Вопросы для закрепления теоретического материала к практическому занятию:

1.    По какой формуле находится площадь полной поверхности призмы?

2.    По какой формуле находится площадь полной поверхности пирамиды?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.