
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Тема:
Решение задач по теме: «Правила и формулы дифференцирования, таблица производных элементарных функций».
Цель работы:
- применить умения по владению представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей.
Оборудование:
1. Рабочая тетрадь в клетку
2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.
3. Калькулятор простой.
4. Ручка.
Задание:
I Вариант II Вариант
Пользуясь формулами и правилами дифференцирования, найдите производные
|
а) |
а) |
|
б) |
б) |
|
в)
|
в)
|
|
г) |
г) |
|
д) |
д) |
|
е)
е) |
е)
|
|
ж)
|
ж) |
|
з)
|
з)
|
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Производной функции f(x) в точке х называется предел разностного отношения ![]() при
при ![]() .
.
![]() .
.
Операция нахождение производной называется дифференцированием.
Это правило является основным, т.к. выведено из самого определения. Однако при дифференцировании сложных функций, суммы, произведения, частного применение общего правила представляет большие трудности. Поэтому применяют правила дифференцирования.
Правила:
1. ![]() -
Производная суммы равна сумме производных.
-
Производная суммы равна сумме производных.
2. ![]() -
Постоянный множитель можно вынести за знак производной.
-
Постоянный множитель можно вынести за знак производной.
3. ![]() - Производная
произведения.
- Производная
произведения.
4. 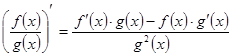 Производная
частного
Производная
частного
Формулы дифференцирования
1.
С′ =
0 11. ![]()
2.
( х ) ′ =
1 12. ![]()
3.
( х 2 ) ′ =
2х 13. ![]()
4. ( х 3) ′ = 3х2
5.
( х р ) ′ = р х р – 1
14. ![]()
6.
( е х ) ′ = е х![]() 15.
15. ![]()
7. ![]() 16.
16. ![]()
8. 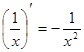 17.
17.
![]()
9. ![]() 18.
18.
![]()
10. ![]()
При выполнении практической работы рассмотрите следующие примеры:
Примеры:
Пользуясь формулами и правилами дифференцирования, найдите производные
1) ![]()
![]()
2) ![]()
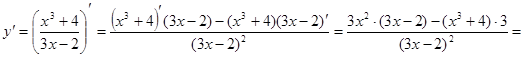
![]() .
.
3) ![]()
![]()
4) ![]()
![]()
5) ![]()
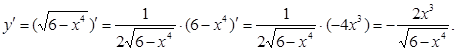
6) ![]()
![]()
7) ![]()
![]()
8) ![]()
![]()
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется производной функции?
2. Какая операция называется дифференцированием?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.
2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
7. Башмаков М.И. Математика: Учебник. — М., 2016.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.