МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Различные виды многогранников. Их изображения. Сечения, развертки многогранников».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Различные виды многогранников. Их изображения. Сечения, развертки многогранников».

Цель работы: 

- применить умения по владению основными понятиями пространственных геометрических фигурах, их основных свойствах − владение;

- применить умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант

1)   Сторона основания правильной четырёхугольной призмы равна а, а диагональ призмы образует с плоскостью основания угол 45º. Найти:

а)  диагональ призмы;

б)  площадь сечения призмы плоскостью, проходящей через сторону нижнего основания и    противоположную сторону верхнего основания.

2)   В правильной треугольной пирамиде сторона основания равна а, а высота равна h. Найдите боковое ребро пирамиды, угол между боковым ребром и плоскостью основания пирамиды.

3) Дан тетраэдр DABC. Точка М – середина ребра AD. Построить сечение тетраэдра плоскостью, проходящей через т.М и параллельно грани АВС. Найти периметр сечения, если ребро тетраэдра равно а.

II Вариант

1)    Диагональ правильной четырёхугольной призмы равна а и образует с плоскостью основания угол в 30º. Найти:

а) сторону основания призмы,

б) площадь сечения призмы плоскостью, проходящей через диагонали основания призмы.

2)   В правильной четырёхугольной пирамиде сторона основания равна а,  плоский угол при вершине равен α. Найти боковое ребро пирамиды.

3)   Дан тетраэдр DABC. Точка М – середина ребра AВ. Построить сечение тетраэдра плоскостью, проходящей через т.М и параллельно грани DВС. Найти периметр сечения, если ребро тетраэдра равно а.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Призма - это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани - параллелограммами.

Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани - боковыми гранями призмы.

При изображении пространственных фигур необходимо соблюдать следующие требования.

1.      Изображение должно быть наглядным. Призму надо изображать так, чтобы наибольшее число её граней были видимыми, чтобы не сливались рёбра.

2.      Изображение должно быть простым, т.е. не должно содержать каких-либо построений, не имеющих прямого отношения к решению задачи. Видимые линии должны иметь наибольшую толщину, невидимые – изображать штриховыми линиями.

3.      Выполнение чертежа призмы удобно начинать с верхнего основания, т.к. в верхнем основании все линии видимые, боковые рёбра изображаются в виде параллельных и равных отрезков.

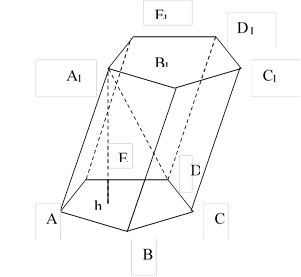
ABCDE A₁ B₁ C₁ D₁ – наклонная призма.

ABCDE   и  A₁ B₁ C₁ D₁ E₁  - основания призмы

АВВ₁ А_{1 …} -  боковые грани (параллелограммы)

АА₁ , ВВ₁ ,  …   -   боковые рёбра

h  -   высота призмы

А₁ D – диагональ призмы

При изображении пространственных фигур необходимо соблюдать следующие требования.

4.  Изображение должно быть наглядным. Пирамиду надо изображать так, чтобы наибольшее число её граней были видимыми, чтобы не сливались рёбра.

5.  Изображение должно быть простым, т.е. не должно содержать каких-либо построений, не имеющих прямого отношения к решению задачи. Видимые линии должны иметь наибольшую толщину, невидимые – изображать штриховыми линиями.

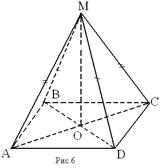
MABCD – четырёхугольная пирамида

М – вершина пирамиды,  

ABCD  -  основание, 

MAB,  MBC, MCD, MAD – боковые грани

MA,   MB,   MC,  MD -  боковые рёбра

MО - высота

Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок соединяющий вершину пирамиды с центром основания, является её высотой.

Все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

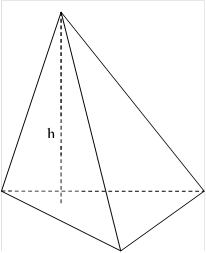
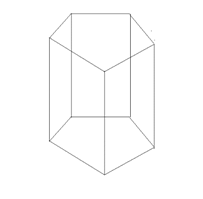
Если боковые рёбра призмы перпендикулярны к основаниям, то призма является прямой. Высота прямой призмы равна её боковому ребру.

Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

Для решения  задач на построение сечений многогранника, надо знать основные понятия.

Опр.

Секущей плоскостью называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.

Секущая плоскость пересекает грани многогранника по отрезкам.

Опр.

Многогранник, сторонами которого являются эти отрезки, называется сечением многогранника. Так как тетраэдр имеет 4 грани, то его сечениями могут быть только треугольники и четырехугольники.   

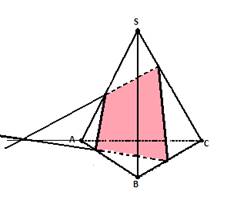
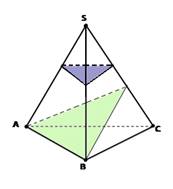
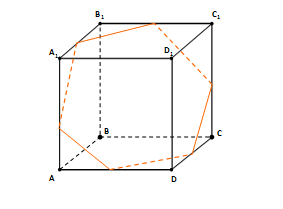
Параллелепипед имеет 6 граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.

При построении сечений параллелепипеда следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны.     

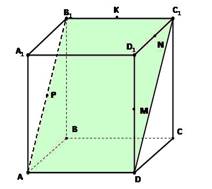
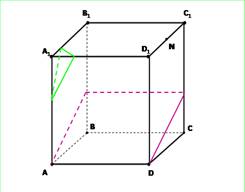
При выполнении практической работы рассмотрите следующую задачу:

Задача:

Точка М лежит на боковой грани АDВ. Построить сечение тетраэдра плоскостью, проходящей через точку М и параллельно основанию АВС.

Решение

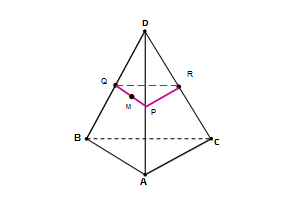
α  - секущая плоскость.

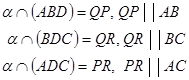
Отсюда вытекает следующий способ построения искомого сечения.

Проведём через точку М прямую, параллельную отрезку АВ,  и обозначим буквами P  и Q точки пересечения этой прямой  с боковыми рёбрами  DA и  DB. Затем через точку Р проведём прямую, параллельную отрезку АС, и обозначим буквой  R точку пересечения  этой прямой с ребром DC. Треугольник PQR – искомое сечение.

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Что называется призмой?

2.    Что называется пирамидой?

3.    Какая плоскость называется секущей?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016