МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме «Свойства линейной, квадратичной, кусочно-линейной и дробно – линейной функций».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме «Свойства линейной, квадратичной, кусочно-линейной и дробно – линейной функций».

Цель работы: 

- применить умения строить графики и проводить исследования линейно квадратичной, кусочно-линейной, дробно- линейной функции.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

𝗅 Вариант                                                                       𝗅𝗅 Вариант

1. Постройте график функций и проведите исследование

a) y = 2x – 3                                                                                 y = -3x +1                                                                              

б)y = x²+4x+5                                                                                     y = x²-6x+10

в)y =                                                                                         y =

г) y =                                              y =

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Дробно-линейная функция и ее график                                                                                  

 Дробно-линейная функция – это функция вида y =                                                                                       

где x – переменная, a, b, c, d – некоторые числа, причем c ≠ 0, ad – bc ≠ 0.

Свойства дробно-линейной функции:

1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными.

2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными.

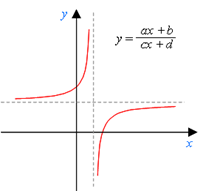
 Графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы y = k/x с помощью параллельных переносов вдоль координатных осей.

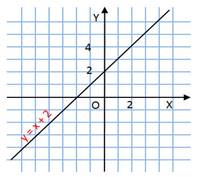
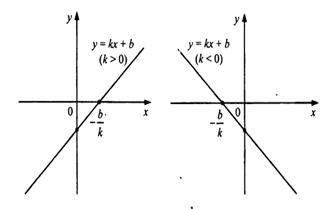
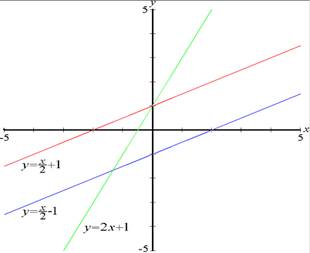
Линейная функция — функция вида y = kx + b

Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.

Графиком линейной функции является прямая линия, с чем и связано её название. Это касается вещественной функции одной вещественной переменной. Частный случай  линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от  — неоднородных линейных функций.

Квадратичная функция — функция вида f(x) = ax² + bx+c. где a≠ 0.и a, b, c некоторые числа.

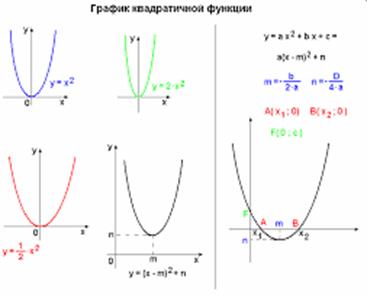
График квадратичной функции называют параболой.

В общем виде уравнение квадратичной функции записывается так: y = ax²+bx+c. Координаты вершины параболы: (x₀;y₀),x₀ = -  , y₀ = -                                                                                 

Прямая  является осью симметрии графика квадратичной функции.

При a < 0  ветви параболы направлены вниз, при a > 0  — вверх.

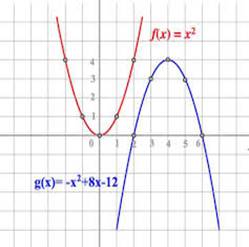
Кусочно-линейная функция [piecewise linear function] — нелинейная функция f(x) = f(x1, x2, …, xn), которая (при ее геометрическом представлении) состоит из переходящих друг в друга линейных участков.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

y = x²-4x+3

Находим координаты вершины параболы:

x =  =  = 2

y = 2²-4·2+3 = 4-8+3 = -1

(2; -1) – вершина параболы.

Находим точки пересечения графика с осью  ox:

x²-4x+3 = 0

x₁ = 1 и x₂ = 3.

Строим график.

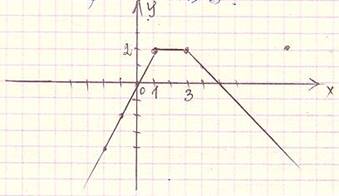
Пример 2:

y =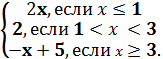

Вопросы для закрепления теоретического материала к практическому занятию:

1. Определение и свойства линейной функции.

2. Определение и свойства квадратичной функции.

3. Определение кусочно-линейной функции.

4.Определение и свойства дробно-линейной функции.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.