МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Угол между прямой и плоскостью. Теорема о трех перпендикулярах».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Угол между прямой и плоскостью. Теорема о трех перпендикулярах».

Цель работы: 

- применить  умения и навыки применения изученных теоретических фактов в ходе решения задач

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1

№ 1. Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках  D и Е соответственно, причем АС ║α. Найдите АС, если ВD : AD = 3 : 4 и  DE = 10 см .

№ 2. Отрезок АВ пересекает плоскость α, точка С – середина АВ. Через точки А, В и С проведены параллельные прямые, пересекающие плоскость α в точках А₁, В₁ и С₁. Найдите СС₁, если  дм и ВВ₁ = √2 дм. 

№ 3. Сторону СD треугольника CDE пересекают плоскости α и β, параллельные стороне СЕ соответственно в точках К и Р, а сторону DE – в точках М и N, причем DК вдвое меньше РК, а СР вдвое больше РК. Найдите СЕ, если КМ = 6 см.

№ 4. Треугольник МКN равносторонний со стороной, равной 18 см. Точка С удалена от вершин треугольника МКN на 12 см. Найдите расстояние от точки С до плоскости МКN.

№ 5. АВСD – квадрат. Точка М удалена от сторон квадрата на  см. Найдите периметр квадрата, если точка М удалена от плоскости АВС на  см.

№ 6. Плоскость α перпендикулярна плоскости β. Точка А принадлежит плоскости α. Отрезок АА₁ – перпендикуляр к плоскости β, точка В принадлежит плоскости β и ВВ₁ -  перпендикуляр к плоскости α. Найдите АВ, если АА₁ = 8 см, ВВ₁ = 12 см, А₁В₁ = см.

№ 7. АВСDA₁В₁С₁D₁ – куб. Найдите расстояние между прямыми АВ₁ и ВС, если ребро куба равно см.

Вариант 2.

№ 1. Плоскость β пересекает стороны МР и КР треугольника МРК соответственно в точках  N и Е, причем MK ║ β. Найдите NE, если MK = 12 см и  MN : NP = 3 : 5.

№ 2. Отрезок CD пересекает плоскость β, точка E – середина CD. Через точки C, D и E проведены параллельные прямые, пересекающие плоскость β соответственно в точках C₁, D₁ и E₁. Найдите EE₁, если  cм  и  DD₁ = √3 cм.

№ 3. Плоскости α и β, параллельные стороне АВ треугольника АВС, пересекают сторону АС соответственно в точках N и М, а сторону ВС – в точках Е и К. Отрезок МN в три раза больше отрезка СN, а отрезок АМ вдвое короче МN. Найдите АВ, если NЕ = 12 см.

№ 4. Треугольник АСD -  равносторонний. Точка S удалена от вершин треугольника ACD на 6 см, а от плоскости треугольника АСD на 3 см. Найдите сторону треугольника АСD.

№ 5. АВСD – квадрат с периметром, равным 16 см. Точка Е удалена от всех сторон квадрата на 4 см. Найдите расстояние точки Е от плоскости АВС.

№ 6. Плоскость α перпендикулярна к плоскости β. Точка С принадлежит плоскости α. Отрезок СС₁ – перпендикуляр к плоскости β, точка D принадлежит плоскости β и DD₁ -  перпендикуляр к плоскости α. Найдите длину отрезка С₁D₁, который принадлежит линии пересечения плоскостей α и β, если СС₁ = 8 см, DD₁ = 12 см, СD = 15 см.

№ 7. АВСDA₁В₁С₁D₁ – куб, ребро которого равно см. Найдите расстояние между прямыми СС₁ и DВ₁.

Порядок выполнения:

1.   Внимательно прочитать тему и цель практической работы.

1.        Изучить учебный материал по теме.

2.        Ответить на вопросы.

3.        Выполнить задания.

4.        Подготовить отчет.

Пояснения к работе (учебный материал):

Углом между наклонной к плоскости (прямая PO) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P'O.)

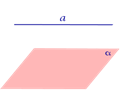
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

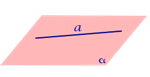
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

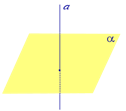
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

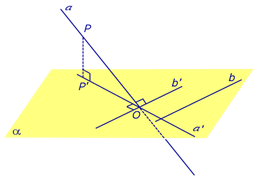
Теорема о трех перпендикулярах

      Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a' на плоскость α перпендикулярна к прямой b.

    Доказательство. Рассмотрим следующий рисунок:

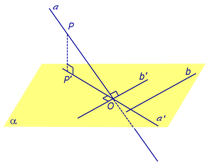
На рисунке  буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P' – это проекция точки P на плоскость α. Проведем через точку O прямую b', параллельную прямой b. Если прямая b проходит через точку O, то прямая b', совпадет с прямой b.

      Поскольку PP' – перпендикуляр к плоскости α, то прямая PP' перпендикулярна к прямой b'. Прямая a перпендикулярна к прямой b' по условию. Таким образом, прямая b' перпендикулярна к двум пересекающимся прямым PO и PP', лежащим в плоскости POP'. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b' перпендикулярна к плоскости POP', откуда вытекает, что прямая b' перпендикулярна и к прямой a', лежащей на плоскости POP'. Теорема доказана.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

 Дано: ΔАВС; АВ = АС = ВС; CD ⊥ (ABC); AM = MB, DM = 15, CD = 12 (рис. 3).

Найти: SΔADB.

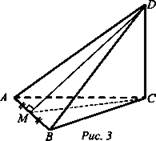
Решение:

1) CD ⊥ (ABC) ⇒ CD ⊥ AC и CD ⊥ ВС, тo есть ∠ACD = ∠BCD = 90° и ΔADC, ΔBDC -прямоугольные.

2) ΔADC = ΔBDC (по двум катетам): DC - общий, AC = ВС (по условию). Значит, AD = BD (как соответствующие в равных треугольниках), тогда ΔADB - равнобедренный (по определению) и DM - медиана. Следовательно, DM - высота (по свойству медианы равнобедренного треугольника).

3) DC ⊥ МС ⇒ ∠DCM = 90° и ΔMCD - прямоугольный. По теореме Пифагора: MD2 = DC2 + МС2. Тогда 

4) ΔМСВ - прямоугольный (∠CMB = 90°, так как СМ - медиана и высота в ΔАВС - равностороннем),  тогда 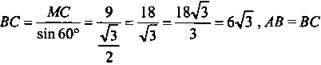 (по условию),

5)  (Ответ: 45√3.)

Пример 2:

Дан тетраэдр МАВС, угольный, где D ∈ AC, MB ⊥ АВ. Найдите MD и S_MBD, если MB = BD = а.

Дано: МАВС - тетраэдр; MB ⊥ АВ, MB ⊥ ВС; D ∈ AC, MB = BD = а (рис. 4).

Доказать: ΔMBD - прямоугольный.

Найти: MD; S_MBD.

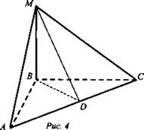
Решение: Так как  то MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).

Значит,   (по определению прямой, перпендикулярной плоскости), то есть ∠MBD = 90°, а значит, ΔMBD - прямоугольный.

2) ΔMBD, по теореме Пифагора: 

3)  (Ответ: )

Вопросы для закрепления теоретического материала к практическому занятию:

1. Угол между прямой и плоскостью  (перечислите все возможные случаи)

2. Сформулируйте теорему о трех перпендикулярах?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.

Скачано с www.znanio.ru