МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Виды симметрий в пространстве. Симметрия тел вращения и многогранников».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Виды симметрий в пространстве.  Симметрия тел вращения и многогранников».

Цель работы: 

- применить умения по владению основными понятиями пространственных геометрических фигурах, их основных свойствах − владение;

- применить умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант

1.  При зеркальной симметрии прямая  а отображается на прямую  а₁ . Докажите, что прямые а и а₁  лежат в одной плоскости ( прямые  а и а₁  параллельны ).

2.  При зеркальной симметрии относительно плоскости α  плоскость β отображается на плоскость β₁ . Докажите, что если  β ║ α , то  β₁║ α.

3.  Докажите, что при параллельном переносе на вектор   р, где р ≠ 0 , прямая , не параллельная вектору р и не содержащая этот вектор, отображается на параллельную ей прямую.

II Вариант

1.  При зеркальной симметрии прямая  а отображается на прямую  а₁ . Докажите, что прямые а и а₁  лежат в одной плоскости ( прямые  а и а₁  пересекаются ).

2.  При зеркальной симметрии относительно плоскости α  плоскость β отображается на плоскость β₁ . Докажите, что если  β перпендикулярна α , то  β₁ совпадает с  β.

3.  Докажите, что при параллельном переносе на вектор   р, где р ≠ 0 , прямая , параллельная вектору р или содержащая этот вектор, отображается на себя.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

При решении задач на движение пространства, надо знать виды движения. Это центральная симметрия, осевая симметрия, зеркальная симметрия и параллельный перенос.

Опр. (центральная симметрия)

Точки М и М₁ называются симметричными относительно т О (центр симметрии), если О – середина отрезка ММ₁. Точка О считается симметричной самой себе.

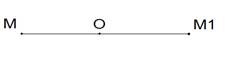т. М и т.М₁  симметричны относительно т.О.

т. О – центр симметрии

т.О – середина отрезка ММ₁

т.О отображается сама на себя

Опр. ( осевая симметрия)

Точки А и А₁  называются симметричными относительно прямой а ( ось симметрии), если прямая а проходит через середину отрезка АА₁  и перпендикулярна к этому отрезку.  Каждая точка прямой а считается симметричной самой себе.

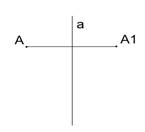
Опр. ( зеркальная симметрия)

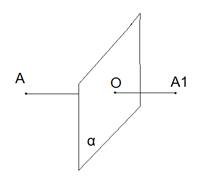
Точки АА₁ называются симметричными относительно плоскости α( плоскость симметрии), если плоскость  α  проходит через середину отрезка АА₁ и перпендикулярна к этому отрезку. Каждая точка плоскости считается симметричной самой себе.

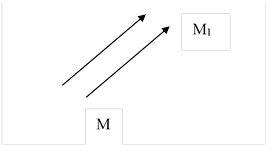
Опр .   Параллельным переносом на вектор называется отображение пространства на себя, при котором любая точка М переходит в точку М₁ , что

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Какая симметрия называется осевой?

2.    Какая симметрия называется зеркальной?

3.    Какая симметрия называется центральной?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.