МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Вычисление площадей и объемов.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Вычисление площадей и объемов.

Цель работы: 

- применить умения по владению основными понятиями пространственных геометрических фигурах, их основных свойствах − владение;

- применить умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант

1.   Диагональ правильной четырёхугольной призмы равна 4 см и составляет с плоскостью боковой грани угол 30º . Найдите объём призмы.

2.   Апофема правильной четырёхугольной пирамиды равна 3 см, плоский угол при вершине 60º. Найти объём пирамиды.

3.   Радиус шара равен 4 см. Через конец радиуса, лежащий на сфере, проведена плоскость под углом 30º к нему. Найти площадь сечения шара.

4.   Радиус основания цилиндра, описанного около сферы, равен 2. Найти разность между площадью поверхности цилиндра и сферы.

II Вариант

1.   Найти объём прямоугольного параллелепипеда, у которого стороны основания равны 12 см и 16 см, а диагональ параллелепипеда составляет 45º с плоскостью основания.

2.   В правильной четырёхугольной пирамиде боковое ребро составляет с плоскостью основания угол 45º . Сторона основания пирамиды равна 6 см. Найти объём пирамиды.

3.   Образующая конуса 14 см, и наклонена к плоскости основания под углом в 60º. Найти площадь поверхности конуса.

4.   Площадь осевого сечения цилиндра равна 20 см². Найти площадь его боковой поверхности.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

1.      Объём куба вычисляется по формуле:   , где а – ребро куба.

2.      Объём прямоугольного параллелепипеда вычисляется по формуле:   ,

      где а, в, с – измерения прямоугольного параллелепипеда (длина, ширина, высота)

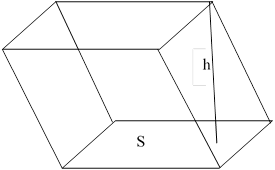
3.      Объём призмы  равен   

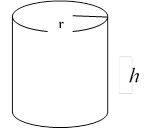
4.   Объём цилиндра вычисляется по формуле:  

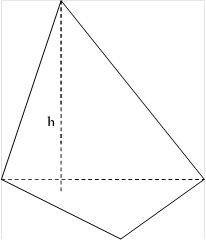
1.      Объём пирамиды вычисляется по формуле:  ,   где  S – площадь основания, h - высота

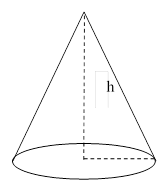
       2.   Объём конуса вычисляется по формуле:  ,   где  S – площадь основания, h – высота

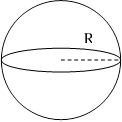
3.       Объём шара равен:          R³ 

                     4.   Площадь поверхности призмы равна

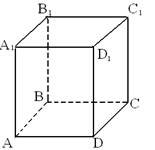
  Площадь боковой поверхности прямой призмы равна произведению периметра основания на

       высоту.

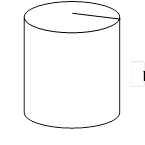
5.   Площадь поверхности цилиндра равна       

           , где    r -  радиус цилиндра,      h -высота цилиндра

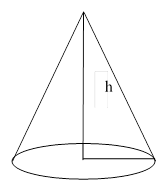
 4.   Площадь поверхности конуса равна                     

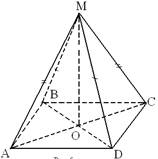
6.    Площадь поверхности пирамиды:   

7.   Площадь поверхности шара:  

Вопросы для закрепления теоретического материала к практическому занятию:

1.    По какой формуле находится объем призмы?

2.    По какой формуле находится объем пирамиды?

3.    По какой формуле находится объем цилиндра?

4.    По какой формуле находится объем конуса?

5.    По какой формуле находится объем шара?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.