Методические проблемы изучения тригонометрии.

Фирсова Светлана Ивановна

МБОУСОШ с. Высокое

Башмаковского района

Пензенской области

учитель математики

Методические проблемы изучения тригонометрии.

На сегодняшний день отечественной школой накоплен богатый опыт изучения элементов тригонометрии как в старшей школе (тригонометрические функции), так и в основной (решение треугольников), имеются интересные методические подходы, разработаны системы учебных заданий.

Однако на современном этапе возникает множество новых проблем, особенно при обучении старшеклассников, связанных, в первую очередь, с тем, что соответствующее содержание школьной тригонометрии носит преобладающий алгоритмический характер. Вследствие этого к нему формируется отношение как к учебному материалу, не имеющему отношения к развитию школьника.

Но тригонометрический материал весьма интересен и специфичен, так как он находится на стыке геометрии и алгебры. Пожалуй, ни один школьный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Уже несколько десятилетий тригонометрия, как отдельная дисциплина школьного курса математики не существует, она плавно растеклась не только в геометрию и алгебру основной школы, но и в алгебру и начала анализа. По мнению вузовских преподавателей, выпускники школ тригонометрию знают плохо, так как большинство учащихся школы отождествляют тригонометрию с набором огромного числа жутких формул, которые ни один нормальный человек запомнить не в состоянии. Такое представление о тригонометрии складывалось у нас в школе десятилетиями. Мы стали понимать, что основная задача учителя математики - развитие умственных способностей обучающегося, а не заполнение ячеек его памяти формулами. В этой связи настало время пересмотреть тригонометрические методические традиции.

Тригонометрия - это красивый и законченный раздел, но, чтобы придать ему цельность и стройность, надо положить в его основание три камня, «три кита тригонометрии»: числовая окружность, простейшие тригонометрические уравнения и теорема сложения.

В школьном курсе математики использовались разные варианты введения тригонометрических функций. При этом большинству учебных пособий присущ один и тот же недостаток-недооценка важности изучения самой модели «числовая окружность» и слишком поспешное, чуть ли не на первом уроке, введение понятий синуса и косинуса «по окружности», что приводит к наложению двух трудностей: непривычная модель (числовая окружность) и непривычный способ введения функций (синус как ордината, косинус как абсцисса точки числовой окружности). При этом упор делается на геометрический материал о вычислении длин дуг окружностей, поэтому многие учащиеся испытывают затруднения с геометрическим истолкованием основных компонентов «тригонометрического языка» (2π–длина числовой окружности , –длина четверти окружности и т. д.).

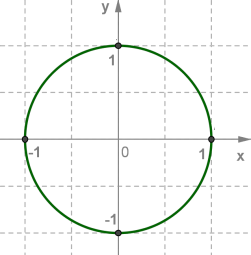
Целесообразно выделить числовую окружность в качестве самостоятельного объекта изучения, т. к. на самом деле школьникам приходится изучать не одну, а две новые модели: первая - числовая окружность, вторая - числовая окружность на координатной плоскости. Предлагаю уделить достаточно времени «дидактическим играм» с этими двумя моделями, а также уделить большое внимание подготовке к введению основных определений: длине дуги единичной окружности, модели «числовая окружность» и модели «числовая окружность на координатной плоскости». Для успешного овладения указанными моделями можно предложить систему специальных заданий - «дидактических игр».

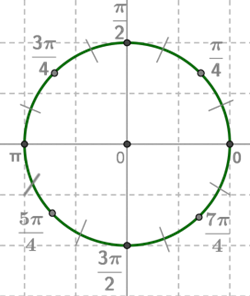
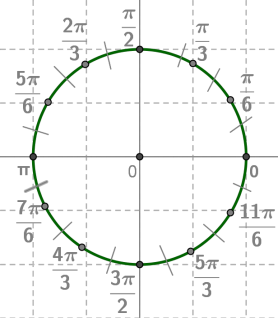
Первая игра – отыскание на числовой окружности точек, соответствующих заданным числам, выраженным в долях числа π (,  и т. д. ), и составление двух макетов числовой окружности: на первом из них все четверти разделены пополам с указанием главных имен точек, на втором – все четверти разделены на три равные части ( тоже с указанием главных имен ). Эти макеты полезно вывесить в кабинете математики. Обязательно обсудить с учащимися вопрос: что будет, если по каждому из макетов точка движется не в положительном, а в отрицательном направлении. Тогда на обоих макетах выделенным точкам придется присвоить другие имена. Игра завершается осмыслением главного отличия числовой окружности от числовой прямой: на прямой соответствие между точками и числами взаимно-однозначное, на окружности у каждой точки бесконечно много имен вида t = t₀ + 2πk, где t₀ – главное имя.

Вторая игра – отыскание на числовой окружности точек, соответствующих заданным числам, не выраженным в долях числа π, - речь идет о построении точек М (1), М (2), …, М (6), М (-7) и при желании более экзотических точек типа М (49).

Третья игра – составление аналитической записи (двойных неравенств) для дуг числовой окружности.

         Рассмотрим для примера открытую дугу MP, где M – середина первой четверти, а P- середина второй четверти. Неравенства, характеризующие дугу, т. е. представляющие собой аналитическую модель дуги, предлагаю составлять в два шага. На первом шаге составляем ядро аналитической записи ( это главное, чему следует научить школьников ); для заданной дуги MP получим    t  . На втором шаге составляем общую запись:

 + 2πk  t   + 2πk.

         Если же речь идет о дуге PM, то при записи ядра нужно учесть, что точка А (0) лежит внутри дуги, а потому к началу дуги нам приходится двигаться по первой отрицательной окружности. Значит, ядро аналитической записи дуги PM имеет вид -   t  , а общая запись имеет вид

-  + 2πk  t   + 2πk.

Четвертая игра – отыскание декартовых координат точек числовой окружности, центр которой совмещен с началом системы координат.

При изучении модели «числовая окружность на координатной плоскости» школьникам приходится работать одновременно в двух системах координат – в «криволинейной», когда информация о положении точки снимается по окружности, и в декартовой прямоугольной системе координат, что вызывает трудности обучающихся. Задача учителя – помочь в преодолении этих естественных трудностей. Предлагаю с первых уроков преподавания тригонометрии использовать символы sin t, cos t, tg t, ctg t, т. к. буква x в сознании школьника четко ассоциируется с абсциссой в декартовой прямоугольной системе координат, а не с длиной пройденного по числовой окружности пути.

В процессе этой игры речь идет о переходе от записи M (t) к записи M (x, y), т. е. к переходу от криволинейных координат к декартовым. Например,

M () = M ( ;  ).

Фактически мы готовим школьников к вычислению значений тригонометрических функций. Если здесь все будет отработано достаточно хорошо, то переход на новую ступень (ордината – синус, абсцисса – косинус) окажется менее болезненным.

Четвертая игра включает в себя и задания типа: для точки М (5) найти знаки декартовых координат.

Пятая игра – отыскание на числовой окружности точек по заданным условиям. Например: y =   или x . Фактически учитель готовит школьников к решению простейших тригонометрических уравнений и неравенств.

После введения определений синуса и косинуса как координат точки числовой окружности целесообразно снова поиграть в третью, четвертую и пятую игры, но уже с использованием введенных обозначений: вычислить sin , решить уравнение cos t = , решить неравенство sin t  0,5 и т. д.