Методические указания для организации самостоятельной работы по учебной дисциплине «Математика»

Государственное бюджетное профессиональное образовательное учреждение

 «Коми-Пермяцкий политехнический техникум»

 

Рассмотрено	Утверждаю
На заседании ПЦК протокол №	Зам. дир. по УР
«_____»______________2015г.	_________Н.Ф.Борисова
	«___»__________2015г.

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы   по учебной дисциплине «Математика»

основной профессиональной образовательной программы

в соответствии ФГОС по профессиям НПО

 

 

/29.01.05/           Закройщик

/23.01.03/           Автомеханик

/29.01.29/           Мастер столярного и мебельного производства

/08.01.14/           Монтажник санитарно-технических систем и оборудования

/08.01.06/           Мастер сухого строительства

/15.01.05/           Сварщик

/08.01.19/           Электромонтажник по силовым сетям и электрооборудованию

/15.01.25/           Станочник (металлообработка)

                                                              

                                                                                                Составила:  Плотникова В.И.

преподаватель математики         

 

 

 

 

 

 

 

 

 

 

 

2015

 

Пояснительная записка

Методические рекомендации для организации внеаудиторной самостоятельной работы по дисциплине «Математика» предназначены для обучающихся первого  и  второго курса по профессиям НПО:

/29.01.05/           Закройщик

/23.01.03/           Автомеханик

/29.01.29/           Мастер столярного и мебельного производства

/08.01.14/           Монтажник санитарно-технических систем и оборудования

/08.01.06/           Мастер сухого строительства

/15.01.05/           Сварщик

/08.01.19/           Электромонтажник по силовым сетям и электрооборудованию

/15.01.25/           Станочник (металлообработка)

 

Основная задача профессионального образования заключается в формировании творческой личности специалиста, способного к саморазвитию, самообразованию, инновационной деятельности. Решение этой задачи вряд ли возможно только путем передачи знаний в готовом виде от преподавателя к обучающемуся. Необходимо перевести обучающегося из пассивного потребителя знаний в активного их творца, умеющего сформулировать проблему, проанализировать пути ее решения, найти оптимальный результат и доказать его правильность. Следует признать, что самостоятельная работа обучающихся является не просто важной формой образовательного процесса, а должна стать его основой.

В соответствии с учебным планом на самостоятельную работу обучающихся отводится не менее 50 % аудиторной нагрузки, т.е.145 часов.

Целью самостоятельной работы обучающихся является:

-     обеспечение профессиональной подготовки выпускника в соответствии с ФГОС СПО;

-     формирование и развитие общих компетенций, определённых в ФГОС СПО;

-     формирование и развитие профессиональных компетенций, соответствующих основным видам профессиональной деятельности.

Задачами, реализуемыми в ходе проведения внеаудиторной самостоятельной работы обучающихся, в образовательной среде техникума являются:

-       систематизация, закрепление, углубление и расширение полученных теоретических знаний и практических умений студентов;

-       развитие познавательных способностей и активности студентов: творческой  инициативы, самостоятельности, ответственности и организованности;

-       формирование самостоятельности мышления: способности к саморазвитию, самосовершенствованию и самореализации;

-       овладение практическими навыками применения информационно-коммуникационных технологий в профессиональной деятельности;

-       развитие исследовательских умений.

 

Виды самостоятельной работы обучающихся  по математике

-         решение заданий по образцу;

-         опережающие домашние задания;

-         выполнение заданий по алгоритму;

-         типовые расчеты;

-         решение экзаменационных вариантов, в том числе ЕГЭ;

-         составление алгоритмов для типовых заданий;

-         составление и решение самостоятельно составленных заданий;

-         выполнение графических работ;

-         составление и заполнение таблиц для систематизации учебного материала;

-         составление теста и эталона к нему;

-         ответы на контрольные вопросы;

-         составление или решение математического кроссворда на математические

понятия, определения и т.п.;

-         творческие работы (реферат, доклад, сообщение, сочинение);

-         изготовление геометрических фигур;

-         разработка проекта, включающего элементы самостоятельного исследования и направленного на поиск новых методов решения поставленных задач (например, «Математика в моей профессии»).

Возможные формы контроля

-       проверка выполненной работы преподавателем;

-       отчет-защита обучающегося по выполненной работе перед преподавателем (и/или обучающимися  группы);

-       зачет;

-       тестирование;

-       контрольные работы.

Критериями оценки результатов самостоятельной работы

 обучающихся  являются:

-       уровень усвоения обучающимся  учебного материала;

-       умение обучающегося  использовать теоретические знания при выполнении практических задач;

-       сформированность ключевых (общеучебных) компетенций;

-       обоснованность и четкость изложения материала;

-       уровень оформления работы.

Указания к выполнению ВСР

 

1.      ВСР нужно выполнять в отдельной тетради в клетку, чернилами черного или синего цвета. Необходимо оставлять поля шириной 5 клеточек для замечаний преподавателя.

2.      Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.

3.      Оформление решения задачи следует завершать словом «Ответ».

4.      После получения проверенной преподавателем работы обучающийся должен в этой же тетради исправить все отмеченные ошибки и недочеты. Вносить исправления в сам текст работы после ее проверки запрещается.

5.      Оценивание индивидуальных образовательных достижений по результатам выполнения ВСР  производится в соответствии с универсальной шкалой (таблица).

 

 

 

Методические рекомендации по составлению конспекта

 

Внимательно прочитайте текст. Уточните в справочной литературе непонятные слова. При записи не забудьте вынести справочные данные на поля конспекта.

Выделите главное, составьте план.

Кратко сформулируйте основные положения текста, отметьте аргументацию автора.

Законспектируйте материал, четко следуя пунктам плана. При конспектировании старайтесь выразить мысль своими словами. Записи следует вести четко, ясно.

Грамотно записывайте цитаты. Цитируя, учитывайте лаконичность, значимость мысли.

 

Методические рекомендации по выполнению практических занятий

 

Для того чтобы практические занятия приносили максимальную пользу, необходимо помнить, что упражнение и решение ситуативных задач проводятся по вычитанному на лекциях материалу и связаны, как правило, с детальным разбором отдельных вопросов лекционного курса. Следует подчеркнуть, что только после усвоения лекционного материала с определенной точки зрения (а именно с той, с которой он излагается на лекциях) он будет закрепляться на практических занятиях как в результате обсуждения и анализа лекционного материала, так и с помощью решения ситуативных задач. При этих условиях студент не только хорошо усвоит материал, но и научится применять его на практике, а также получит дополнительный стимул (и это очень важно) для активной проработки лекции.

При самостоятельном решении поставленных задач нужно обосновывать каждый этап действий, исходя из теоретических положений курса. Если обучающийся видит несколько путей решения проблемы (задачи), то нужно сравнить их и выбрать самый рациональный. Полезно до начала решения поставленных задач составить краткий план решения проблемы (задачи). Решение проблемных задач или примеров следует излагать подробно, нужно сопровождать комментариями, схемами, чертежами и рисунками, инструкциями по выполнению.

Следует помнить, что решение каждой учебной задачи должно доводиться до окончательного логического ответа, которого требует условие, и по возможности с выводом. Полученный результат следует проверить способами, вытекающими из существа данной задачи. 

 

 

Методические рекомендации по написанию контрольной работы

 

Контрольная работа – промежуточный метод проверки знаний обучающегося с целью определения конечного результата в обучении по данной теме или разделу. Она предназначена систематизировать знания, позволяет повторить и закрепить материал. При выполнении студенты ограничены во времени, могут использовать любые учебные пособия, консультации преподавателя.

 

Методические рекомендации к написанию реферата

Требования к содержанию:

- материал, использованный в реферате, должен относится строго к выбранной теме;

- необходимо изложить основные аспекты проблемы не только грамотно, но и в соответствии с той или иной логикой (хронологической, тематической, событийной и др.)

- при изложении следует сгруппировать идеи разных авторов по общности точек зрения или по научным школам;

- реферат должен заканчиваться подведением итогов проведенной исследовательской  работы: содержать краткий анализ-обоснование преимуществ той точки зрения по рассматриваемому вопросу, с которой Вы солидарны.

 

Структура реферата.

1. Начинается реферат с титульного листа.

Образец оформления титульного листа для реферата:

 

 

 

ГБПОУ «Коми-Пермяцкий политехнический техникум»

 

 

 

 

 

 

 

 

 

 

РЕФЕРАТ

по учебной дисциплине: « Математика»

на тему: «Указать тему реферата»

 

 

 

 

 

 

 

 

                                                        

 

 

 

 

 

 

г. Кудымкар, 20___ г.

 

2. За титульным листом следует Оглавление. Оглавление - это план реферата, в котором каждому разделу должен соответствовать номер страницы, на которой он находится.

3. Текст реферата. Он делится на три части: введение, основная часть и заключение.

а) Введение - раздел реферата, посвященный постановке проблемы, которая будет рассматриваться и обоснованию выбора темы.

б) Основная часть - это звено работы, в котором последовательно раскрывается выбранная тема. Основная часть может быть представлена как цельным текстом, так и разделена на главы. При необходимости текст реферата может дополняться иллюстрациями, таблицами, графиками, но ими не следует "перегружать" текст.

в) Заключение - данный раздел реферата должен быть представлен в виде выводов, которые готовятся на основе подготовленного текста. Выводы должны быть краткими и четкими. Также в заключении можно обозначить проблемы, которые "высветились" в ходе работы над рефератом, но не были раскрыты в работе.

4.  Список источников и литературы. В данном списке называются как те источники, на которые ссылается обучающийся при подготовке реферата, так и все иные, изученные им в связи с его подготовкой. В работе должно быть использовано не менее 5 разных источников, из них хотя бы один – на иностранном языке (английском или французском). Работа, выполненная с использованием материала, содержащегося в одном научном источнике, является явным плагиатом и не принимается. Оформление Списка источников и литературы должно соответствовать требованиям библиографических стандартов (см. Оформление Списка источников и литературы).

Объем и технические требования, предъявляемые к выполнению реферата.

Объем работы должен быть, как правило, не менее 12 и не более 20 страниц. Работа должна выполняться через одинарный интервал 12 шрифтом, размеры оставляемых полей: левое - 25 мм, правое - 15 мм, нижнее - 20 мм, верхнее - 20 мм.  Страницы должны быть пронумерованы.

Расстояние между названием части реферата или главы и последующим текстом должно быть равно трем интервалам. Фразы, начинающиеся с "красной" строки, печатаются с абзацным отступом от начала строки, равным 1 см.

При цитировании необходимо соблюдать следующие правила:

 текст цитаты заключается в кавычки и приводится без изменений, без произвольного сокращения цитируемого фрагмента (пропуск слов, предложений или абзацев допускается, если не влечет искажения всего фрагмента, и обозначается многоточием, которое ставится на месте пропуска) и без искажения смысла;

каждая цитата должна сопровождаться ссылкой на источник, библиографическое описание которого должно приводиться в соответствии с требованиями библиографических стандартов (см. Оформление Списка источников и литературы).

Критерии оценивания реферата:

- соответствие содержания выбранной теме;

- отсутствие в тексте отступлений от темы;

- соблюдение структуры работы, четка ли она и обоснованна;

- умение работать с научной литературой - вычленять проблему из контекста;

- умение логически мыслить;

- культуру письменной речи;

- умение оформлять научный текст (правильное применение и оформление ссылок, составление библиографии);

- умение правильно понять позицию авторов, работы которых использовались при написании реферата;

- способность верно, без искажения передать используемый авторский материал;

- соблюдение объема работы;

- аккуратность и правильность оформления, а также технического выполнения работы.

Реферат должен быть сдан для проверки в установленный срок.

 

Методические рекомендации по подготовке сообщения

 

Сообщение – это сокращенная запись информации, в которой должны быть отражены основные положения текста, сопровождающиеся аргументами, 1–2 самыми яркими и в то же время краткими примерами.

Сообщение составляется по нескольким источникам, связанным между собой одной темой. Вначале изучается тот источник, в котором данная тема изложена наиболее полно и на современном уровне научных и практических достижений. Записанное сообщение дополняется материалом других источников.

Этапы подготовки сообщения:

1. Прочитайте текст.

2. Составьте его развернутый план.

3. Подумайте, какие части можно сократить так, чтобы содержание было понято правильно и, главное, не исчезло.

4. Объедините близкие по смыслу части.

5. В каждой части выделите главное и второстепенное, которое может быть сокращено при конспектировании.

6. При записи старайтесь сложные предложения заменить простыми.

Тематическое и смысловое единство сообщения  выражается в том, что все его компоненты связаны с темой первоисточника.

Сообщение должно содержать информацию на 3-5 мин. и сопровождаться презентацией, схемами, рисунками, таблицами и т.д.

 

Методические рекомендации по составлению презентаций

 

Требования к презентации

На первом слайде размещается:

название презентации;

автор: ФИО, группа, название учебного учреждения (соавторы указываются в алфавитном порядке);

год.       

На втором слайде указывается содержание работы, которое лучше оформить в виде гиперссылок (для интерактивности презентации).

На последнем слайде указывается список используемой литературы в соответствии с требованиями, интернет-ресурсы указываются в последнюю очередь.

 

Оформление слайдов
Стиль	-     необходимо соблюдать единый стиль оформления; -     нужно избегать стилей, которые будут отвлекать от самой презентации; -     вспомогательная информация (управляющие кнопки) не должны преобладать над основной информацией (текст, рисунки)
Фон	-     для фона выбираются более холодные тона (синий или зеленый)
Использование цвета	-     на одном слайде рекомендуется использовать не более трех цветов: один для фона, один для заголовков, один для текста; -     для фона и текста используются контрастные цвета; -     особое внимание следует обратить на цвет гиперссылок (до и после использования)
Анимационные эффекты	-     нужно использовать возможности компьютерной анимации для представления информации на слайде; -     не стоит злоупотреблять различными анимационными эффектами; анимационные эффекты не должны отвлекать внимание от содержания информации на слайде
Представление информации
Содержание информации	-     следует использовать короткие слова и предложения; -     времена глаголов должно быть везде одинаковым; -     следует использовать минимум предлогов, наречий, прилагательных; -     заголовки должны привлекать внимание аудитории
Расположение информации на странице	-     предпочтительно горизонтальное расположение информации; -     наиболее важная информация должна располагаться в центре экрана; -     если на слайде располагается картинка, надпись должна располагаться под ней
Шрифты	-     для заголовков не менее 24; -     для остальной информации не менее 18; -     шрифты без засечек легче читать с большого расстояния; -     нельзя смешивать разные типы шрифтов в одной презентации; -     для выделения информации следует использовать жирный шрифт, курсив или подчеркивание того же типа; -     нельзя злоупотреблять прописными буквами (они читаются хуже, чем строчные).
Способы выделения информации	Следует использовать: -     рамки, границы, заливку -     разные цвета шрифтов, штриховку, стрелки -     рисунки, диаграммы, схемы для иллюстрации наиболее важных фактов
Объем информации	-     не стоит заполнять один слайд слишком большим объемом информации: люди могут единовременно запомнить не более трех фактов, выводов, определений. -     наибольшая эффективность достигается тогда, когда ключевые пункты отражаются по одному на каждом отдельном слайде.
Виды слайдов	Для обеспечения разнообразия следует использовать разные виды слайдов: с текстом, с таблицами, с диаграммами.

 

Критерии оценки презентации

 

Критерии оценки	Содержание оценки
1. Содержательный критерий	правильный выбор темы, знание предмета и свободное владение текстом, грамотное использование научной терминологии, импровизация, речевой этикет
2. Логический критерий	стройное логико-композиционное построение речи, доказательность, аргументированность
3. Речевой критерий	использование языковых (метафоры, фразеологизмы, пословицы, поговорки и т.д.) и неязыковых (поза, манеры и пр.) средств выразительности; фонетическая организация речи, правильность ударения, четкая дикция, логические ударения и пр.
4. Психологический критерий	взаимодействие с аудиторией (прямая и обратная связь), знание и учет законов восприятия речи, использование различных приемов привлечения и активизации внимания
5. Критерий соблюдения дизайн-эргономических требований к компьютерной презентации	соблюдены требования к первому и последним слайдам, прослеживается обоснованная последовательность слайдов и информации на слайдах, необходимое и достаточное количество фото- и видеоматериалов, учет особенностей восприятия графической (иллюстративной) информации, корректное сочетание фона и графики, дизайн презентации не противоречит ее содержанию, грамотное соотнесение устного выступления и компьютерного сопровождения, общее впечатление от мультимедийной презентации

 

 

 

 

Методические рекомендации по составлению кроссворда

 

Кроссворд-это игра, состоящая в разгадывании слов по определениям.

 

1.     В общем случае определение должно состоять из одного предложения.

2.     Определения должны быть по во возможности краткими. Следует избегать перечислений, не злоупотреблять причастными и деепричастными оборотами, не перегружать текст прилагательными. Определение кроссворда - своего рода компромисс между краткостью и содержательностью.

3.     Запрещается использование в одной сетке двух и более одинаковых слов, даже с различными определениями.

4.     В вопросах следует избегать энциклопедических определений. В целом работа должна быть авторской, а не перепечаткой статей из словаря.

5.     Нежелательно начинать формулировку вопроса с цифры, глагола, деепричастия.

6.     Запрещается использование однокоренных слов в вопросах и ответах.

7.     В работе должна быть изюминка, то есть нечто, отличающее ее от миллионов других.

8.   Запрещается помещать слова без пересечений (встречается и такое).

 Не используются слова, пишущиеся через тире и имеющие уменьшительно-ласкательную окраску.

Требования к оформлению кроссворда:

-         На каждом листе должна быть фамилия автора, а также название данного кроссворда;

-         Рисунок кроссворда должен быть четким;

-         Сетки всех кроссвордов должны быть выполнены в двух экземплярах:

1-й экз. - с заполненными словами;

2-й экз. - только с цифрами позиций.

Ответы публикуются отдельно. Ответы предназначены для проверки правильности решения кроссворда и дают возможность ознакомиться с правильными ответами на нерешенные позиции условий, что способствует решению одной из основных задач разгадывания кроссвордов — повышению эрудиции и увеличению словарного запаса.

Критерии оценивания составленных кроссвордов:

1.       Четкость изложения материала, полнота исследования темы;

2.       Оригинальность составления кроссворда;

3.       Практическая значимость работы;

4.       Уровень стилевого изложения материала, отсутствие стилистических ошибок;

5.       Уровень оформления работы, наличие или отсутствие грамматических и пунктуационных ошибок;

6.       Количество вопросов в кроссворде, правильное их изложение.

 

Перечень тем внеаудиторной самостоятельной работы

Название разделов, тем внеаудиторной самостоятельной работы	Количество часов	Вид деятельности	Формы контроля
Раздел 1. Развитие понятия числа. Самостоятельная работа №1. «Решение заданий с точным учетом погрешностей. Самостоятельная работа №2. «История открытия комплексных чисел». Самостоятельная работа №4. «Тригонометрическая и показательная форма комплексных чисел». Самостоятельная работа №5. «Действия над комплексными числами»	10 2     3     2     3	Выполнение  заданий   Создание  презентации   Работа с учебной литературой   Решение заданий	Проверка выполненных заданий   Просмотр и оценка презентаций   Проверка конспекта     Проверка выполненных заданий
Раздел 2. Степенная функция. Самостоятельная работа №6. «Графическое решение уравнений и неравенств». Самостоятельная работа №7. «Примеры функциональных зависимостей в реальных процессах и явлениях». Самостоятельная работа №8. «Иррациональные уравнения. Уравнения, содержащие переменную под знаком модуля».	8   3     2     3	Работа с учебной литературой   Выполнение  реферата   Работа с учебной литературой	Проверка конспекта     Проверка и защита рефератов   Проверка конспекта и выполненных заданий
Раздел 3. Корни, степени и логарифмы. Самостоятельная работа №9. «Значение и история понятия логарифма». Самостоятельная работа №10  «Графики показательной и логарифмической функций» Самостоятельная работа № 11. «Решение заданий на преобразование логарифмических выражений». Самостоятельная работа №12. «Решение показательных и логарифмических уравнений и неравенств».	12   4     2     3     3	Выполнение  реферата   Построение  графиков функций Решение заданий     Решение уравнений и неравенств	Проверка и защита рефератов   Проверка выполненных заданий   Проверка выполненных заданий   Проверка выполненных заданий
Раздел 4.  Основы тригонометрии Самостоятельная работа № 13   «Модель тригонометрического круга» Самостоятельная работа №14. «История развития и становления тригонометрии». Самостоятельная работа №15. «Решение тригонометрических уравнений повышенной сложности». Самостоятельная работа № 16 «Преобразование графиков тригонометрических функций»	17 3     6     6     2	Изготовление  модели   Выполнение  реферата Решение  уравнений     Графическая  работа	Проверка заданий     Проверка и защита рефератов   Проверка выполненных заданий   Проверка выполненных заданий
Раздел 5. Прямые и плоскости в пространстве. Самостоятельная работа №17. «Прямые и плоскости в пространстве». Самостоятельная работа № 18. «Взаимное расположение прямых и плоскостей в пространстве».	10   4     6	Создание  презентации   Составление кроссворда	Просмотр и оценка презентаций   Проверка кроссворда
Раздел 6. Координаты вектора. Самостоятельная работа № 19. «Действия над векторами». Самостоятельная работа № 20. «Решение задач по теме «Векторы»».	6 3   3	Создание  презентации Решение задач	Просмотр и оценка презентаций Проверка выполненных заданий
Раздел 7. Многогранники. Самостоятельная работа № 21. «Правильные многогранники». Самостоятельная работа № 22. «Жизнь и творчество Эйлера». Самостоятельная работа № 23. «Многогранники». Самостоятельная работа № 24. «Звездчатые многогранники. Кристаллы-природные многогранники». Самостоятельная работа № 25. «Модели многогранников».	26 4   4   4   4     10	Создание  презентации Выполнение  реферата Создание  презентации Подготовить  сообщения   Изготовление  моделей	Просмотр и оценка презентаций Проверка и защита рефератов Просмотр и оценка презентаций Выступление с сообщением на занятии   Оценивание изготовленных моделей
Раздел 8 Тела вращения. Поверхности и объемы тел вращения. Самостоятельная работа № 26. «Цилиндр и конус». Самостоятельная работа № 27. «Шар и сфера». Самостоятельная работа № 28. «Площадь поверхности частей шара». Самостоятельная работа № 29. «Модели тел вращения». Самостоятельная работа № 30. «Объемы тел» Самостоятельная работа № 30 Решение задач с профессиональной направленностью	21   4   4   3     4   3   3	Создание презентации Создание  презентации Работа с учебной литературой   Изготовление  моделей Решение задач   Решение задач	Просмотр и оценка презентаций Просмотр и оценка презентаций Проверка конспекта     Оценивание изготовленных моделей Проверка выполненных заданий Проверка выполненных заданий
Раздел 9. Начала математического анализа. Самостоятельная работа № 31. «Способы задания и свойства числовой последовательности. Понятие о пределе последовательности. Бесконечно убывающая геометрическая последовательность и ее сумма». Самостоятельная работа № 32. «Производная и ее применение». Самостоятельная работа № 33. «Предел, связанный с числом e». Самостоятельная работа № 34. «Решение прикладных задач». Самостоятельная работа № 35. «Интеграл и его применение». Самостоятельная работа № 36. «Приближенные методы вычисления определенного интеграла».	25   3           5   3   4   6   4	Работа с учебной литературой         Создание  презентации Работа с учебной литературой. Решение задач   Создание  презентации Работа с учебной литературой	Проверка конспекта           Просмотр и оценка презентаций Проверка конспекта   Проверка выполненных заданий Просмотр и оценка презентаций Проверка конспекта
Раздел 10. Комбинаторика. Элементы теории вероятностей Самостоятельная работа № 37. «Жизнь и научная деятельность И. Ньютона». Самостоятельная работа № 38. «Я. Бернулли». Самостоятельная работа № 39. «Решение задач по теории вероятностей».	10   4     2   4	Выполнение  реферата   Выполнение  реферата Решение задач	Проверка и защита рефератов   Проверка и защита рефератов Проверка выполненных заданий
Итого:	145	-	-

 

 

 

Раздел 1. Развитие понятия числа

 

Самостоятельная работа № 1.

Решение заданий с точным учетом погрешности

 

Цель: Знать правила действия над приближенными числами с точным учетом погрешности.

 

Методические рекомендации

 

Правила для выполнения действий с точным учетом погрешности:

1.                  4.

2.                   5.

3.

Применив правила для выполнения действий с точным учетом погрешности, выполните действия:

 

1. Найдите сумму  и разность , если:

а) ; 

б) ;  

в) ;     

2. Найдите произведение  и частное , если:

а)  с точностью до  0,5%;   с точностью до 1%;

б) с точностью до  1%;   с точностью до 0,5%;

в)  с точностью до 0,1%;   с точностью до 1%.

3. Масса ящика с содержимым равна кг, масса пустого ящика равна кг. Найти массу содержимого в ящике..

4. Найти площадь прямоугольника ширины  и длины, если м и м с точностью до 1%.

5. Найти степень , если  с точностью до 2,5%.

6. Найти , если  с точностью до 2,5%.

 

Самостоятельная работа № 2.

История открытия комплексных чисел

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

Методические рекомендации

Работа должна соответствовать методическим рекомендациям по созданию презентаций.

 

Самостоятельная работа № 3.

Тригонометрическая и показательная форма записи комплексных чисел

 

Цель: Знать тригонометрическую и показательную форму записи комплексных чисел и уметь выполнять действия над к.ч., заданными этими формами.

 

1. Изучив тему, письменно ответьте на вопросы:

 

1⁰. Запись к.ч. в тригонометрической форме.

2⁰. Формулы перехода от алгебраической формы к.ч. к тригонометрической и   наоборот.

3⁰. Действия над к.ч. в тригонометрической форме.

4⁰. Запись к.ч. в показательной форме.

5⁰. Формулы перехода от алгебраической формы к.ч. к показательной и наоборот.

6⁰. Действия над к.ч. в показательной форме.

7^0. Выполните письменно упр. №5, стр. 20

 

Литература: М.И. Башмаков Математика: учебник для студ. Учреждений сред. проф. образования /М.И. Башмаков. – 9-е изд., стер. – М.: Издательский центр «Академия», 2014.-256 с.,Гл 1, Занятие 4.

 

Самостоятельная работа № 4.

Решение задач по теме: «Действия над комплексными числами»

 

Цель: Уметь выполнять действия над к.ч., заданными разными формами.

 

Методические рекомендации

 

Формы комплексного числа.

1. Алгебраическая

сложение:

умножение:

деление:

2. Тригонометрическая

умножение:

деление:

возведение в степень:

извлечение корня: ,  

3. Показательная

умножение:

деление: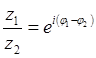

возведение в степень:

Используя методические рекомендации, выполните задания:

 

1 вариант	2 вариант
1. Найдите, если ,	1. Найдите , если ,
2. Найдите модуль к.ч.	2. Найдите модуль к.ч.
3. Найдите , если ,	3. Найдите , если ,
4. Вычислите:	4. Вычислите:
5. Разложите на множители: а) ; б)	5. Разложите на множители: а); б)
6. Решите уравнения: а); б)	6. Решите уравнения: а) ; б)
7. Выполнить умножение, деление и возведение в степень к.ч. , если а) ,   б) ;	7. Выполните умножение, деление и возведение в степень к.ч. , если а) , б) ;
8. Запишите в тригонометрической и показательной форме к.ч. а) ; б)	8. Запишите в тригонометрической и показательной форме к.ч. а) ; б)

 

 

Раздел 2. Степенная функция.

Самостоятельная работа № 5.

Графическое решение уравнений и неравенств

 

Цель: Уметь с помощью графика находить решение уравнений и неравенств.

 

Изучив тему, письменно ответьте на вопросы:

 

1. Графическая интерпретация решения уравнения .

2. Графическая интерпретация решения неравенства.

3. Определение числа корней уравнения   (графическое).

4. Записать решение прим.18, с. 193.

 

Литература: М.Я. Пратусевич «Алгебра и начала математического анализа»  10кл., М., «Просвещение», 2014,  с.193.

 

Самостоятельная работа № 6.

Примеры функциональных зависимостей

в реальных процессах и явлениях   

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной  деятельности: подготовить реферат по предложенной теме.

 

Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферата.

 

Самостоятельная работа № 7.

Иррациональные уравнения. Уравнения и неравенства с модулем

 

Цель: Знать правила избавления от иррациональности, раскрытия модуля числа и уметь пользоваться ими при решении уравнений и неравенств.

 

Методические рекомендации

 

Формулы для повторения:                               

;

;

Решение квадратных уравнений:

,

Если  то

Если  то

Если  то корней нет

;           ;          ;             ;         ;     

1. Изучив тему, письменно ответьте на вопросы:

 

1⁰. Введите понятие иррационального уравнения.

2⁰. Сформулируйте утверждение и замечание на с.350.

3⁰. Решение уравнений, содержащих квадратные радикалы.

4⁰. Записать решение примера 60, с. 351.

5⁰. Метод уединения радикалов (прим. 61).

6⁰. Сформулируйте утверждение на с. 352.

7⁰. Дайте определение  и его иной формы.

8⁰. Таблица решения элементарных уравнений и неравенств с модулем.

9⁰. Записать решение примера 85, с. 74.

10⁰. Запишите вывод о решении неравенства с модулем.

11⁰. Запишите решение примера 90, с. 76.

 

2. Выполните письменно задания:

 

1 вариант	2 вариант
1. Решите уравнения: а) ; б) ; в) .	1. Решите уравнения: а) ; б) ; в) .
2. Решите уравнения: а) ;  б) .	2. Решите уравнения: а) ;  б) .
3. Решите неравенства: а) ;  б) .	3. Решите неравенства: а) ;  б) .

 

Литература: М.Я. Пратусевич «Алгебра и начала анализа», 10кл., М., «Просвещение» 2014, гл. I,  §10; 11кл.-гл.XIII, §84.

 

 

Раздел 3. Показательная и логарифмическая функции.

 

Самостоятельная работа № 8.

Значение и история понятия логарифма

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить реферат по предложенной теме.

 

Методические рекомендации

Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферата.

 

Самостоятельная работа № 9

Графики показательной и логарифмической функций

Цель: уметь выполнять преобразования графиков показательной и логарифмической функций

Методические рекомендации

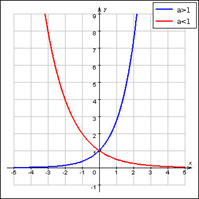
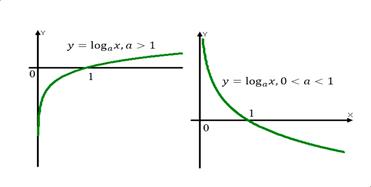у=а^х

 

 

 

 

Задание: используя методические указания из самостоятельной работы № 15 постройте график функции.

Вариант 1 Построить график функции	Вариант 2 Построить график функции	Вариант 3 Построить график функции	Вариант 4 Построить график функции
Вариант 5 Построить график функции	Вариант 6 Построить график функции	Вариант 7 Построить график функции	Вариант 8 Построить график функции
Вариант 9 Построить график функции	Вариант 10  Построить график функции	Вариант 11  Построить график функции	Вариант 12 Построить график функции
Вариант 13 Построить график функции	Вариант 14 Построить график функции	Вариант 15 Построить график функции	Вариант 16 Построить график функции
Вариант 17 Построить график функции	Вариант 18 Построить график функции	Вариант 19 Построить график функции	Вариант 20 Построить график функции
Вариант 21 Построить график функции	Вариант 22 Построить график функции	Вариант 23 Построить график функции	Вариант 24 Построить график функции
Вариант 25 Построить график функции	Вариант 26 Построить график функции	Вариант 27 Построить график функции	Вариант 28 Построить график функции

 

Самостоятельная работа № 10.

Решение заданий на преобразование логарифмических выражений

 

Цель: Знать основное логарифмическое тождество, свойства логарифмов, уметь применять их при преобразовании выражений.

 

Методические рекомендации

 

I. Свойства логарифмов.

1. Основное логарифмическое тождество:

2.     

3.

4.

5.

6.

7.

8.  - формула перехода к другому основанию

9.

Используя методические рекомендации, выполните задания:

 

1 вариант	2 вариант
1. Найдите значение числового выражения:	1. Найдите значение числового выражения:
2. Вычислите: а) ; б) ; в)	2. Вычислите: а) ; б) ; в)
3. Найдите log572, если известно, что  log52=a,   log53.	3. Вычислите log530, если известно, что log52=a,   log53=b.
4. Вычислить: а) ; б)	4. Вычислить: а) ; б)

 

Самостоятельная работа № 11.

Решение показательных, логарифмических уравнений и неравенств

 

Цель: Знать методы решения показательных и логарифмических уравнений и неравенств, уметь применять их при решении соответствующих заданий.

 

Методические рекомендации

 

Степени чисел от 0 до 10

n	0	1	2	3	4	5		6	7	8	9	10
	1	2	4	8	16	32		64	128	256	512	1024
	1	3	9	27	81	243		729	2187	6561	19683	59049
	1	4	16	64	256	1024		4096	16384	65536	262144
	1	5	25	125	625	3125		15625	78125	390625
	1	6	36	216	1296	7776		46656	279936
	1	7	49	343	2401	16807		117649
	1	8	64	512	4096	32768
	1	9	81	729	6561	59049
	1	10	100	1000	10000
Решение квадратных уравнений:   , Если  то Если  то Если  то корней нет							Формулы сокращенного умножения:
Свойства степеней							Свойства корней n-ой степени
1.        2.        3.        4.        5.      6.      7.      8.        9.							1.        2.        3.        4.        5.        6.      7.

 

Используя предложенные методические рекомендации и методические рекомендации к самостоятельной работе №9, выполните задания:

 

1 вариант	2 вариант
1. Решить уравнения: а) ; б) ; в) ; г) ;      д) .	1. Решить уравнения: а) ;  б) ; в); г); д) .
2. Решить неравенства: а) ; б) ; в) ; г) .	2. Решить неравенства: а) ; б) ; в) ; г) .

 

 

 

 

 

 

Раздел 5. Основы тригонометрии.

 

Самостоятельная работа № 12

Модель тригонометрического круга

Цель: уметь находить точки на единичной окружности

 

Задание: изготовить модель тригонометрического круга на плотной бумаге  формата  А4. Показать линии тангенса и котангенса.

 

Самостоятельная работа № 13.

История развития и становления тригонометрии

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить реферат по предложенной теме.

 

Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферата.

 

Самостоятельная работа № 14.

Решение тригонометрических уравнений повышенной сложности

 

Цель: Знать методы решения тригонометрических уравнений, формулы для нахождения корней, уметь использовать полученные знания при решении уравнений повышенной сложности.

 

Методические рекомендации

 

I. Решение простейших тригонометрических уравнений.

 

II. Тригонометрические уравнения.

 

III. Основные тригонометрические тождества.

1.     ; ;

2.       

3.       

4.        и

5.    

6.    

IV. Формулы сложения.

1.    

2.    

3.    

4.    

5.    

6.    

V. Формулы двойного и половинного аргументов.

1.    

2.     ; ;

3.    

4.    

5.    

6.   

VI. Формулы суммы и разности одноименных тригонометрических функций.

1.    

2.    

3.    

4.    

5.    

 

Значения тригонометрических функций

 

градусная мера угла	00	300	450	600	900
радианная мера угла	0
	0				1
	1				0
	0		1		-
	-		1		0

 

Используя методические рекомендации, решите уравнения:

 

1. ;

2.;

3.;

4.;

5.;

6. .

 

Подсказки.

1. Воспользуйтесь формулой двойного угла для и .

2. Обозначьте  , решите уравнение, сведя его к квадратному с помощью формулы .

3. Сгруппируйте 1-ое и 3-е слагаемые, примените разложение на множители.

4. Воспользуйтесь формулой двойного угла для  и , формулой понижения степени .

5. Раскройте скобки, примените основное тригонометрическое тождество.

6. Приведите дроби к общему знаменателю, а затем используйте основное тригонометрическое тождество , сведите уравнение к квадратному.

 

Самостоятельная работа № 15

Преобразование графиков тригонометрических функций

Цель: уметь выполнять преобразования графиков тригонометрических функций: параллельный   перенос, симметрия  относительно  осей  координат  и  начала  координат, симметрия  относительно прямой  у = х, растяжение  и   сжатие  вдоль  осей)

Методические рекомендации

Функция вида  y=f(x+t) - сдвиг по оси ОХ влево при t>0  и вправо при t<0;

Функция вида y=f(x) +m – сдвиг по оси OY вверх при m>0, вниз при m<0;

Функция вида y = f(kx) – сжатие по оси ОХ при k>1, растяжение при k<1;

Функция вида y = k f(x) –растяжение по оси ОУ при k>1, сжатие при k<1

Задание: используя методические указания постройте график функции

 

 

 

 

Вариант 1 Построить график функции	Вариант 2 Построить график функции	Вариант 3 Построить график функции	Вариант 4 Построить график функции
Вариант 5 Построить график функции	Вариант 6 Построить график функции	Вариант 7 Построить график функции	Вариант 8 Построить график функции
Вариант 9 Построить график функции	Вариант 10  Построить график функции	Вариант 11  Построить график функции	Вариант 12 Построить график функции
Вариант 13 Построить график функции	Вариант 14 Построить график функции	Вариант 15 Построить график функции	Вариант 16 Построить график функции
Вариант 17 Построить график функции	Вариант 18 Построить график функции	Вариант 19 Построить график функции	Вариант 20 Построить график функции
Вариант 21 Построить график функции	Вариант 22 Построить график функции	Вариант 23 Построить график функции	Вариант 24 Построить график функции
Вариант 25 Построить график функции	Вариант 26 Построить график функции	Вариант 27 Построить график функции	Вариант 28 Построить график функции

 

 

 

 

 Раздел 7. Координаты вектора.

 

Самостоятельная работа № 16.

Действия над векторами

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа должна соответствовать методическим рекомендациям по созданию презентации.

 

 

Самостоятельная работа № 17.

Решение задач по теме: «Векторы»

 

Цель: Знать правила действия над векторами и уметь применять их при вычислениях.

 

Методические рекомендации

 

Теоретический материал   

Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим     векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.

 

Теорема. Вектор    имеет координаты (x, y, z) тогда и только тогда,  когда он представим в виде .

 

 

 

Вариант 1

№ п/п	Название операции	Формулы
1	Найти сумму векторов
2	Найти разность векторов
3	Найти произведение вектора на число	,
4	Вычислить координаты середины отрезка	Точка A.  Точка  B (-3;4;-1 .Точка С- середина отрезка АВ. С(;.
5	Найти координаты вектора	Точка A  Точка  B (-1;4;-7.Находим координаты вектора . Из  координат конца вычислить координаты начала вектора
6	Найти длину вектора
7	Вычислить скалярное произведение векторов
8	Найти косинус  угла между векторами
9	При каких значениях  и  векторы коллинеарны?
10	Проверьте перпендикулярность векторов	- условие перпендикулярности векторов

 

Вариант 2

№ п/п	Название операции	Формулы
1	Найти сумму векторов
2	Найти разность векторов
3	Найти произведение вектора на число	,
4	Вычислить координаты середины отрезка	Точка A  Точка  B (2;-3;1 Точка С- середина отрезка АВ. С(,
5	Найти координаты вектора	Точка A  Точка  B (1;-4;7. Находим координаты вектора . Из  координат конца вычислить координаты начала вектора
6	Найти длину вектора
7	Вычислить скалярное произведение векторов
8	Найти косинус  угла между векторами
9	При каких значениях  и  векторы коллинеарны?
10	Проверьте перпендикулярность векторов	- условие перпендикулярности векторов

 

 

 

 

Раздел 8. Прямые и плоскости в пространстве

 

Самостоятельная работа № 18.

Прямые и плоскости в пространстве

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа  должна соответствовать методическим рекомендациям по созданию презентации.

 

Самостоятельная работа № 19.

Составление кроссворда на тему: «Взаимное расположение

прямых и плоскостей в пространстве»

 

Цель: Развитие интереса к предмету, интуиции, логического мышления.

 

Кроссворд-это игра, состоящая в разгадывании слов по определениям.

 

Методические рекомендации

 

При выполнении задания воспользуйтесь методическими рекомендациями по составлению кроссворда.

 

Образец оформления и составления кроссвордов

 

По горизонтали:

 

1. Сторона прямоугольного треугольника.

4. Он есть у функции и последовательности.

8. Его штаны равны во все стороны.

10. Полный круг вращения.

13. Французский математик, специалист теории вероятностей.

14. Арифметическое действие.

16. Гектар — ... площади.

17. Часть матрицы.

18. Свойство углов.

19. Полупрямая.

22. Нейтральный элемент относительно умножения.

23. Группа повторяющихся цифр в бесконечной десятичной дроби.

24. Наибольший общий ...

 

По вертикали:

 

2. Бублик как математический объект.

3. Положение, нуждающееся в доказательстве.

4. Поверхность, имеющая 2 измерения.

5. Линейное алгебраическое уравнение.

6. Тригонометрическая функция.

7. Один из двух экстремумов.

9. Функция по своей сути.

11. Часть прямой.

12. Линия.

15. Геометрическая фигура, образованная двумя лучами.

17. Полный квадрат первого двузначного числа.

18. Для него необходимы натуральные числа.

20. В теории графов: маршрут, все ребра которого различны.

21. В теории графов: замкнутый маршрут, все ребра которого различны.

 

Ответы:

По горизонтали:  1-катет; 4-предел; 8-пифагор; 10-оборот; 13-пуассон; 14-умножение; 16-мера; 17-строка; 18-смежность; 19-луч; 22-единица; 23-период; 24-делитель;

По вертикали: 2-тор; 3-теорема; 4-плоскость; 5-лау; 8-синус; 7-максимум; 9-отображение; 11-отрезок; 12-кривая; 15-угол; 17-сто; 18-счёт; 20-цепь; 21-цикл.

 

Раздел 9. Многогранники.

 

Самостоятельная работа № 20.

Правильные многогранники

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа  должна соответствовать методическим рекомендациям по созданию презентации.

Самостоятельная работа № 21.

Жизнь и творчество Эйлера.

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить реферат по предложенной теме.

 

Реферат должен быть оформлен с соблюдением методических рекомендаций по написанию реферата.

 

 

Самостоятельная работа № 22.

Многогранники

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа  должна соответствовать методическим рекомендациям по созданию презентации.

 

Самостоятельная работа № 23.

Звездчатые многогранники

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить сообщение по предложенной теме.

 

Сообщение должно соответствовать методическим рекомендациям по подготовке сообщений.

 

Самостоятельная работа № 24.

Модели многогранников

 

Цель: Закрепить понятие многогранника при изготовлении моделей, используя развертки.

 

Форма самостоятельной деятельности: изготовление моделей многогранников.

 

Методические рекомендации

 

Одним из способов изготовления правильных многогранников является способ с использованием, так называемых, развёрток.

Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника. Для получения модели многогранника удобно сначала изготовить развёртку его поверхности.  При этом необходимыми инструментами являются клей и ножницы. Мо­дели многогранников можно сделать, поль­зуясь одной разверткой, на которой будут расположены все грани. Однако в этом случае все грани будут одного цвета.

 

 

Используя методические рекомендации, изготовьте модели изученных вами многогранников.

 

 

 

 

Раздел 9. Тела вращения. Поверхности и объемы тел вращения.

 

Самостоятельная работа № 25.

Цилиндр и конус

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа  должна соответствовать методическим рекомендациям по созданию презентации.

 

Самостоятельная работа № 26.

Шар и сфера

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа  должна соответствовать методическим рекомендациям по созданию презентации.

 

 

Самостоятельная работа № 27.

Площадь поверхности частей шара

 

Цель: Знать определение частей шара, формулы для нахождения их площадей. Уметь применять полученные формулы для решения задач.

 

Методические рекомендации

 

                  

 

1. Изучив тему, ответьте на вопросы:

 

1⁰. Дайте определение шарового сегмента.

2⁰. Дайте определение шарового пояса.

3⁰. Дайте определение шарового сектора.

4⁰.  Запишите формулы для нахождения площадей поверхностей частей шара.

 

2. Решите задачи:

 

1⁰. Найдите площадь поверхности шарового сегмента, отсекаемого от шара радиуса 2, плоскостью проходящей на расстоянии 1от центра шара.

2⁰. Шар радиуса 1 пересечен двумя параллельными плоскостями, которые делят перпендикулярный им диаметр шара в отношении 1:2:3. Определите площадь поверхности шара, заключенную между секущими плоскостями.

 

Литература: 1. А.Д. Александров «Геометрия»,11кл., 2014, М., «Просвещение», с. 94, с. 117.

                       2. Г.Н. Яковлев «Математика для техникумов. Геометрия», М., «Наука», 1987, гл. VII, §92.

 

 

Самостоятельная работа № 28.

Модели тел вращения

 

Цель: Закрепить понятие тел вращения при изготовлении моделей, используя развертки.

 

Форма самостоятельной деятельности: изготовление моделей тел вращения.

 

Методические рекомендации

 

Одним из способов изготовления тел вращения является способ с использованием, так называемых, развёрток.

Если модель поверхности тела вращения изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по образующей, отделить основание и развернуть так, чтобы она превратится в модель некоторого многоугольника плюс круг. Эту фигуру называют развёрткой поверхности тела вращения. Для получения модели тела вращения удобно сначала изготовить развёртку его поверхности.  При этом необходимыми инструментами являются клей и ножницы. Мо­дели тел вращения можно сделать, поль­зуясь одной разверткой, на которой будут расположены все элементы.

 

       

 

 

Используя развертки тел вращения, изготовьте их модели.

 

 

 

 

 

Раздел 11. Объемы многогранников и тел вращения

 

Самостоятельная работа № 29.

Решение задач по теме: «Объемы тел»

 

Цель: Знать формулы для нахождения объемов многогранников и тел вращения.

 

Методические рекомендации

 

Основные формулы

№ п/п	Наименование многогранника	Изображение	Площадь боковой и полной поверхности
1	Куб		V=a3
2	Прямоугольный параллелепипед		V=a*b*c V=Sосн*h
3	Призма		V=Sосн*h
4	Пирамида		V=(1/3)*Sосн*h

 

Теоретический материал

№ п/п	Наименование фигуры	Изображение	Формула площадей полной и боковой поверхности
1	Цилиндр
2	Конус
3	Сфера, шар

 

Используя методические рекомендации, решите задачи:

 

 

1 вариант
1.     Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и высота 4 см.
2.     Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем  данной призмы.
3.     Площадь осевого сечения цилиндра равна 4 м2.  Найдите объем цилиндра.
4.      Высота конуса равна . образующая конуса составляет с плоскостью основания угол в . Найти объем конуса.
5.     Площадь большого круга шара равна 3 см2.  Найдите  объем шара.

 

2 вариант
1.     Найдите  объём правильной треугольной пирамиды со стороной основания 6 см и высотой 1 см.
2.     Найдите  объем прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см.
3.     Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите  объем цилиндра.
4.     Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь объем конуса.
5.     Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите  объем шара.

 

Самостоятельная работа № 30

Решение задач с профессиональной направленностью

Цель: развивать интерес к предмету через профессию

Используя методические рекомендации к самостоятельной работе № 29 решите задачи

 

Для профессии «Автомеханик

1.       Вычислить объём дизтоплива в цистерне диаметром 2м и длиной 3м, если она заполнена на 2/3 объёма

2.       У двигателя ВАЗ 21083 диаметр цилиндра 82 мм, ход поршня 71 мм, всего 4 цилиндра. Найти объём двигателя.

3.       Определить ёмкость масляного бака насоса гидроусилителя автомобиля ЗИЛ – 130, если диаметр его 126 мм, а высота 140 мм 

4.       На сколько увеличится объём камеры сгорания двигателя автомобиля ГАЗ – 53, если диаметр поршня 10 см, а ход поршня 9 см?

 

Для профессии «Мастер сухого строительства»

1.     Сколько часов потребуется маляру для окраски панели высотой 2м в помещении (высота 2,7 м, ширина 2,4 м, длина 5 м) маховой кистью или валиком, если норма времени для окраски 100 м² поверхности: кистью –6,4 часа, валиком – 3,4 часа. К данной задаче можно предложить чертеж помещения.

2.     Сколько литров побелки надо налить в емкость для краскопульта диаметром 20 см и высотой 60 см.

3.     Длина комнаты 7 м 60 см, а ширина 6 м. Сколько рулонов обоев потребуется для оклейки, если длина рулона 10 м при ширине 50 см.

4.     Рассчитайте расход масляной краски, идущей на окраску панели помещения (высота 3м, ширина 4м, длина 5м, высота панели 2,2м), если на окраску 1м² требуется 0,2 кг (окна и двери занимают 12% площади поверхности).

 

Для профессии «Сварщик»

1.     Каких размеров потребуется лист железа для изготовления ящика без крышки длиной 17 см, шириной 11 см и высотой 5 см?

2.     Сколько ящиков без крышек размером 210 мм × 115 мм × 45 мм можно сделать из листа железа размером 110 см × 75 см?

3.     Сколько в пачке электродов для электросварки, если их общее масса 5 кг, а каждый электрод- кусок стальной проволоки длиной 45 см и диаметром 5 мм?

4.     Сколько из листа оцинкованного железа прямоугольной формы размером 150х100 можно сделать бидонов с крышками, имеющих форму прямоугольного параллелепипеда длиной 20 см, шириной 15 см, высотой 30 см, если расход на швы составляет 0,4% всей площади листа?

 

 

Для профессии «Закройщик»

1.     Проем в окне имеет высоту 2 м .45 см и ширину 1 м 58 см. Сколько потребуется ткани шириной 85 см для занавески, закрывающей весь проем окна, если на подшивку одного конца занавески требуется 2 см, на продольный шов по 1 см от полосы и на закрытие стен по краям проема 10 см?

2.     Сколько шпона потребуется для обшивки двух цилиндрических колонн высотой 3,5 м и диаметром 80 см, стоящих в вестибюле здания. На отходы и швы - 10%.

3.     Сколько кожи необходимо на покрышку футбольного мяча радиуса 10 см? (На швы добавить 8 % площади поверхности мяча.)

 

 

Раздел 9. Начала математического анализа.

 

Самостоятельная работа № 30.

Способы задания и свойства числовой последовательности.

Понятие о пределе последовательности. Бесконечно убывающая геометрическая последовательность и ее сумма

 

Цель: Знать определение последовательности и способы ее задания. Иметь понятие о пределе последовательности, бесконечно убывающей геометрической последовательности и ее сумме.

Задание: решить задачи.

Вариант 1 1. Напишите формулу общего члена последовательности натуральных чисел, которые при делении   на 6 дают в остатке 1. 2.  Последовательность  (хn) задана  формулой хn  =  3n – 4. Найдите:     а) x1;    б) x5;    в) x12;    г) x100;  д)  xn + 1. 3. Последовательность задана формулой       an = 7n -  5.    а) Вычислите первые пять членов этой последовательности.    б) Определите, будет ли число 9 являться членом этой последовательности?    в) Найдите самый близкий к числу 95 член этой последовательности. 4. Найдите сумму геометрической прогрессии bn, если b1=3, q =

Вариант 1 1. Напишите формулу общего члена последовательности натуральных чисел, которые при делении   на 3 дают в остатке 1. 2.  Последовательность  (хn) задана  формулой хn  =  - 3n – 4. Найдите: а) x1;     б) x5;  в) x12;  г) x100;  д)  xn + 1. 3. Последовательность задана формулой       an = 7n +   5.    а) Вычислите первые пять членов этой последовательности.    б) Определите, будет ли число 33являться членом этой последовательности?    в) Найдите самый близкий к числу 95 член этой последовательности. 4.Найдите сумму геометрической прогрессии bn, если b1=2, q =

 

 

Самостоятельная работа № 31.

Производная и ее применение

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа должна соответствовать методическим рекомендациям по созданию презентации.

 

Самостоятельная работа № 32.

Предел, связанный с числом

 

Цель: Знать основу появления числа .

 

1. Изучив тему,  письменно ответьте на вопросы:

 

1⁰. Сформулируйте теорему о существовании предела:

а) ограниченной сверху неубывающей последовательности;

б) ограниченной снизу невозрастающей последовательности.

2⁰. Что такое число(прим. 3, с. 141)?

 

2. Выполните письменно задание: №4.47(а,б,в).

 

Литература: С.М. Никольский «Алгебра и начала математического анализа», 10кл., М., «Просвещение», 2014, §4, п. 4.6.

 

 

Самостоятельная работа № 33.

Приложения производной

 

Цель: Уметь применять определение производной, ее геометрический и механический смысл к решению прикладных задач.

 

Методические рекомендации

Геометрический смысл производной

Угловой коэффициент касательной, проведенной к графику функции f(x) в точке x_○, равен k = f ꞌ(x_○)

Физический смысл первой производной.

Физический смысл производной заключается в том, что мгновенная скорость движения  в момент времени t есть производная пути по времени, т.е.

 

Физический смысл второй производной.

Ускорение прямолинейного движения в данный момент времени есть первая производная скорости по времени или вторая производная пути по времени.

Пример.

 

1. Зависимость пути от времени при прямолинейном движении точки задана уравнением

.

В какой момент времени ускорение движения точки будет равно 24 м/с²?

 

Решение.

а) Найдем скорость движения точки по формуле:

б) Найти ускорение движения точки по формуле:

  

в) Из условия  м/с², найти момент времени:

 

c

Ответ: 6 с.

 

Правила дифференцирования и таблица производных основных функций.

 

Правила.

 

1.	4.
2.	5.
3.	6.

 

Производные основных элементарных функций.

 

1. ,	8.
2.	9.
3.	10.
4.	11.
5.	12.
6.	13.
7.

 

Используя методические рекомендации, выполните задания:

 

Самостоятельная работа №34

Вариант 1 1.Производная функции  равна:     а) ;     б) ;     в) ;     г) . 2.Производная функции  в точке  равна:     а) –1,5;     б) 1,5;     в) –0,75;     г) 0,75. 3.Какая из приведенных функций является     производной функции?     а) ; б) ; в) ; г) . 4. Точка  движется  прямолинейно  по  закону  .  Какой  формулой  задается  скорость  движения  этой  точки  в  момент  времени  t, чему равна скорость при t=2с . 5. Угловой коэффициент касательной, проведенной к  графику функции   в точке с положительной абсциссой , равен 2. Найдите .

Вариант 2 1.Производная функции  равна:      а) ;     б) ;     в) ;     г) . 2.  Производная функции  в точке  равна:      а) 1,2;     б) 2;     в) –1,2;     г) 2,5. 3.  Какая из приведенных функций является производной функции ?  а) ;  б) ; в) ;  г) . 4. Тело  движется  по  прямой  так,  что  его скорость  v (м/с)  изменяется  по  закону  . Какую скорость  приобретает  тело  в  момент,  когда  его  ускорение  равно  12м/с2. 5.Найдите угловой коэффициент касательной, проведенной к параболе  в точке с абсциссой    .

 

 

Самостоятельная работа № 35.

Интеграл и его применение

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа должна соответствовать методическим рекомендациям по созданию презентации.

 

 

Самостоятельная работа №36

Цель: уметь находить площадь криволинейной трапеции по формуле Ньютона-Лейбница

Методические рекомендации

 

Задание: выполнить графическую  работу  «Вычисление площадей фигур с помощью

                интеграла»

Вариант 1 По готовому чертежу найти площадь   заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями .	Вариант 2 1.По готовому чертежу найти площадь    заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями .
Вариант 3 1.По готовому чертежу найти площадь     заштрихованной фигуры.   2. Вычислите площадь фигуры, ограниченной     линиями	Вариант 4 1.По готовому чертежу найти площадь     заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями
Вариант 5 1. По готовому чертежу найти площадь     заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной  линиями	Вариант 6 1. По готовому чертежу найти площадь     заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями

 

 

 

 

 

Раздел 10. Элементы комбинаторики.

 

Самостоятельная работа № 37.

Жизнь и научная деятельность И. Ньютона

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить реферат по предложенной теме.

 

Реферат должен быть выполнен с соблюдением методическим рекомендациям  по написанию реферата.

 

Раздел 13. Элементы теории вероятностей и математической статистики

 

Самостоятельная работа № 38.

Я. Бернулли

 

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: подготовить реферат по предложенной теме.

 

Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферат.

 

 

Самостоятельная работа № 39.

Повторение. Подготовка к экзамену

 

Цель: Контроль знаний студентов.

 

Выполните письменно задания:

 

1 вариант

 

1.     Отрезок  имеет с плоскостью  единственную общую точку А. Точка С делит его в отношении 3:1, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие  плоскость   соответственно в точках С₁ и В_1. Длина отрезка АС₁  равна 16 см. Найдите длину отрезка АВ₁.

2.     Ромб со стороной 12 см и острым углом 60⁰ вращается около стороны. Найдите объем тела вращения.

3.     Решить уравнение:

4.     Решить систему уравнений:  

5.     Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой  .

6.     Решить уравнение:  

7.     Решите уравнение: 

8.     Найдите все первообразные функции:  

9.     Радиус основания цилиндра  равен 4 см, площадь боковой поверхности вдвое больше площади основания. Найти объем цилиндра.

10. Найдите область определения:     .

 

2 вариант

 

1.     Отрезок  имеет с плоскостью  единственную общую точку А. Точка С делит его в отношении 3:2, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость  соответственно в точках С₁ и В_1. Длина отрезка АС₁  равна 15 см. Найдите длину отрезка АВ₁.

2.     Ромб со стороной 18 см и острым углом 60⁰ вращается около стороны. Найдите объем тела вращения.

3.     Решить уравнение:

4.     Решить систему уравнений:  

5.     Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой  .

6.   Решить уравнение:  

7.     Решите уравнение: 

8.     Найдите все первообразные функции:  

9.     Радиус основания цилиндра  равен 3 см, площадь боковой поверхности  втрое больше площади основания. Найти объем цилиндра.

10. Найдите область определения:     .

 

3  вариант

 

1.     Отрезок  имеет с плоскостью  единственную общую точку А. Точка С делит его в отношении 2:3, считая от точки А. Через точки  С  и В проведены параллельные прямые, пресекающие  плоскость     соответственно в точках С₁ и В_1. Длина отрезка АС₁  равна 20 см. Найдите длину отрезка АВ₁.

2.     Ромб со стороной 24 см и острым углом 60⁰ вращается около стороны. Найдите объем тела вращения.

3.     Решить уравнение:

4.     Решить систему уравнений:  

5.     Найдите угловой коэффициент касательной. Проведенной к графику функции в точке с абсциссой  .

6.     Решить уравнение:  

7.     Решите уравнение: 

8.     Найдите все первообразные функции:  

9.     Радиус основания цилиндра  равен 6 см, площадь боковой поверхности  в четыре раза больше  площади основания. Найти объем цилиндра.

10. Найдите область определения:     .

 

 

Список литературы

 

4.      Александров А.Д. Математика : алгебра и начала математического анализа, геометрия. Геометрия. 10 класс : учеб. для общеобразоват. организаций: углубл. уровень / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М. : Просвещение, 2014. – 271 с.

5.      Александров А.Д. Математика : алгебра и начала математического анализа, геометрия. Геометрия 11 класс : учеб. для общеобразоват. организаций: углубл. уровень / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М. : Просвещение, 2014. – 272 с.

6.      Башмаков М.И. Математика. Задачник : учеб. пособие для студ. учреждений сред. проф. образования / М.И. Башмаков. – 4-е изд., стер. – М. : Издательский центр «Академия» , 2014. – 416 с.

7.      Башмаков М.И. Математика : учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. – 9-е изд., стер. – М. : Издательский центр «Академия», 2014. – 256 с.

8.      Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. : Просвещение, 2014. – 431 с.

9.      Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. : Просвещение, 2014. – 464 с.

10.  Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – М. : просвещение, 2014. – 255 с.

11.  Пратусевич М.Я. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. организаций: углубл. уровень / М.Я. Пратусевич,               К.М. Столбов, А.Н. Головин. – М. : Просвещение, 2014. – 415 с.

12.  Пратусевич М.Я. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций: углубл. уровень / М.Я. Пратусевич,            К.М. Столбов, А.Н. Головин. – М. : Просвещение, 2014. – 463 с.

 

 

 

Скачано с www.znanio.ru