Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный

университет им. Н.И. Лобачевского»

 

Арзамасский филиал

 

Отделение среднего профессионального образования

(Арзамасский политехнический колледж им. В.А. Новикова)

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ

 

по учебной дисциплине

ОП.02 Техническая механика  по специальности:

23.02.03 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ АВТОМОБИЛЬНОГО ТРАНСПОРТА

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Разработчик(и):

 

 

АФ ННГУ отделение СПО

«Арзамасский политехнический

колледж им. В.А. Новикова»             преподаватель                    Д.И Артюхин_________

    (место работы)                        (занимаемая должность)                (инициалы, фамилия)

 

 

 

Содержание

 

Пояснительная записка

Лабораторная работа №1 «Определение реакций опор балки».

Лабораторная работа №2 «Определение коэффициента трения».

Лабораторная работа №3 «Определение τ_nr при кручении».

Лабораторная работа №4 «Определение прогибов балки».

 

 

Пояснительная записка

 

Методические указания предназначены в помощь обучающимся среднего специального образования, входящей в укрупненную группу специальностей при выполнении практических работ  по дисциплине «Техническая механика». Они составлены на основе программы по дисциплине «Техническая механика», разработанной в соответствии с Федеральными государственными образовательными стандартами  для данной специальности.

Дисциплина «Техническая механика» является общепрофессиональной дисциплиной и при ее изучении отводится значительное место решению практических задач, в том числе в рамках проведения практических работ.

Обучающиеся, выполняя практические работы, реализуют следующие цели:

-             обобщать, систематизировать, закреплять полученные теоретические зна­ния по конкретным темам дисциплины;

-             формировать умения применять полученные знания на практике, реализуя единство интеллектуальной и практической деятельности;

-             развивать аналитические, умения у будущих специа­листов;

-             демонстрировать при решении поставленных задач умения, направленные на формирование профессиональных компетенций, предусмотренных программой дисциплины «Техническая механика»;

-             вырабатывать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива, необходимые при формировании общих компетенций.

Использование методических указаний позволяет обучающимся при  минимальных затратах учебного времени самостоятельно выполнять практические работы, даёт возможность преподавателю и обучающимся контролировать и оценивать знания и умения по данной

 

 

Лабораторная работа №1

«Определение реакций опор балки».

Цель работы – ознакомиться с устройством опор балок, составить расчетные схемы балок и определить реакции их опор.

Теоретическое обоснование. Брусом принято считать твердое тело, у которого длина значительно больше поперечных размеров; множество (геометрическое место) центров тяжести всех поперечных сечений называется осью бруса. Брус с прямолинейной осью, положенный на опоры и изгибаемый приложенными к нему нагрузками, называют балкой. Балки встречаются во многих машинах и сооружениях и служат для восприятия сил, направленных перпендикулярно их продольной оси.

Балки имеют специальные опорные устройства для сопряжения их с другими элементами конструкции и передачи на них усилий. Опоры балок можно разделить на следующие три типа:

Подвижная опора (опора на катках) (рис.1, а).

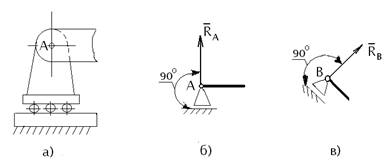
Рисунок 1

Соединение стержня с подвижной опорой допускает поворот стержня вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Здесь известны точка приложения опорной реакции - центр шарнира и ее направление – перпендикуляр к опорной поверхности (трением катков об опорную поверхность пренебрегают). Схематическое изображение подвижной опоры показано на рис.1,б в соответствии с ЕСКД ГОСТ 2.770-68 «Обозначения условные графические в схемах».

Необходимо иметь в виду, что опорная поверхность подвижной опоры может быть не параллельна оси балки (рис.1, в). Реакция опоры в этом случае с осью балки не образует прямой угол.

Шарнирно-неподвижная опора (рис.2, а).

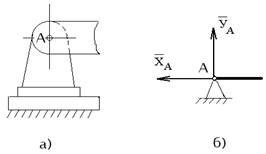
Рисунок 2

Соединение стержня с неподвижной опорой допускает только поворот стержня вокруг оси шарнира. В этом случае известна только точка приложения опорной реакции – центр шарнира, направление реакции неизвестно, так как оно зависит от нагрузки, приложенной к балке. Поэтому вместо полной реакции неподвижной опоры находят ее две взаимно перпендикулярные составляющие и.

Схематическое изображение шарнирно-неподвижной опоры показано на рис.2, б в соответствии с ЕСКД ГОСТ 2.770-68.

Жесткая заделка (защемление) (рис.3, а) не допускает ни линейных перемещений, ни поворота сечений закрепленного балки.

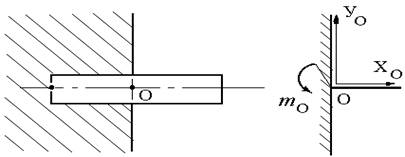
Рисунок 3

Неизвестными для жесткой заделки являются не только направление реакций, но и точки их приложения, поэтому для определения опорной реакции следует найти две взаимно перпендикулярные составляющие ии реактивный моментотносительно центра тяжести опорного сечения балки.

На рис.3, б показано схематическое изображение жесткой заделки.

Равновесие балки под действием любой системы внешних сил, расположенных в одной плоскости, может быть обеспечено одной жесткой заделкой или двумя опорами: подвижной и неподвижной.

На рис.4 показана балка, нагруженная сосредоточенными силами и, равномерно распределенными силами интенсивностьюи парой сил, момент которой равен.

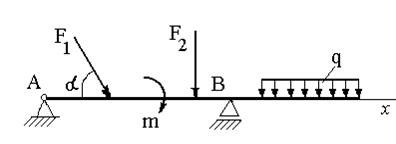
Рисунок 4

Реакции опор балок определяются при помощи трех уравнений равновесия:

; ;. (1)

Приведенная здесь форма уравнений равновесия представляет собой равенство нулю сумм моментов относительно двух точек Аи В – центров шарниров опор балок и равенство нулю суммы проекции на ось х. Ось х совпадает с осью балки.

При определении реакции жесткой заделки опоры целесообразно применить следующую форму трех уравнений равновесия:

; ;. (2)

т.е. равенство нулю проекции всех сил на оси х и у и равенство нулю суммы моментов всех сил относительно точки С.

При определении реакции опор балок целесообразно соблюдать последовательность действий, указанную в таблице 1.

Таблица 1

Последовательность действия при определении реакций опор балок

№п/п	Наименование операций
1	Выделить объект, равновесие которого надо рассмотреть
2	Изобразить расчетную схему: условно изобразить опоры и заданные силы
3	Отбросить опоры (связи), а направление их реакций изобразить на схеме
4	Провести оси координат так, чтобы одна ось была перпендикулярна некоторым неизвестным силам. Наметить центры моментов в точке пересечения линии действия двух неизвестных сил или на линии действия одной неизвестной силы
5	Составить уравнения равновесия	По уравнениям (1) или (2)
6	Решить уравнения равновесия и определить неизвестные силы
7	Проверить правильность решения по уравнению равновесия, которое не было использовано при решении задачи

Экспериментально опорные реакции балок можно определить на специальной установке, позволяющей воспроизводить заданную систему сил, приложенную к балке, а величину и направление реакций опор фиксировать силоизмерительными приборами.

Установка для испытания. Величину и направление реакций опор балки можно определить опытным путем на установке, показанной на рисунке 5. Балка 2 опирается на подвижную опору 8. При помощи блока 7, грузов 5, 6 и винтов 9 можно в любой точке оси балки прикладывать силы, направленные перпендикулярно оси балки и под углом . Балка опирается на резиновые кольца, наполненные цветной жидкостью. Величина реакции опоры соответствует высоте столбике окрашенной жидкости в трубках 1 и 3. Трубка 3 связана с подвижной опорой А и направлена всегда перпендикулярно опорной плоскости, а трубка 1 может поворачиваться вокруг оси неподвижной опоры В. Угол отклонения оси трубки от вертикали соответствует направлению реакции неподвижной опоры.

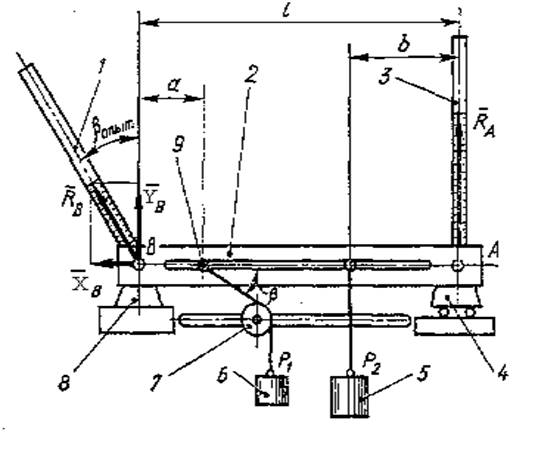
Рисунок 5

Порядок выполнения работы. Ознакомиться с устройством опор балок и их условным изображением. В отчете начертить схему балки и изобразить силы, приложенные к ней. Схема балки и силы выбираются по таблице 2 в соответствии с вариантом задания.

Вычислить величину и направление реакции опор балки.

Произвести экспериментальную проверку полученных результатов на установке.

При помощи грузов приложить к балке заданную систему сил. Силы, направленные перпендикулярно оси балки, создаются грузиками, подвешенными на гибкой нити непосредственно к балке, а силы, направленные под углом, - нитями, перекинутыми через блок. Угол между нитью и осью балки определяется при помощи транспортира. Величина и направление реакции опор определяются по шкалам установки. Направление реакции неподвижной опоры определяется по углу отклонения оси трубки.

Таблица 2

Варианты задания по определению реакций опор балки

№ варианта	Силы,		Отношение расстояний		Угол , град
1	2	3	4	5	6
1	2	7	0,2	0,3	15
2	3	4	0,1	0,2	20
3	4	5	0,5	0,1	25
4	6	2	0,4	0,3	35
5	8	1	0,3	0,1	40
6	1	8	0,2	0,5	45
7	2	7	0,15	0,2	50
8	3	6	0,25	0,3	55
9	4	5	0,3	0,15	60
10	5	4	0,4	0,25	15
11	5	3	0,2	0,1	20
12	7	2	0,1	0,25	25
13	8	1	0,3	0,4	30
14	5	1	0,15	0,3	35
15	4	2	0,25	0,25	40
16	6	3	0,2	0,2	45
17	7	4	0,3	0,3	50
18	8	5	0,4	0,4	55
19	4	6	0,15	0,15	60
20	3	7	0,1	0,2	15
21	2	8	0,35	0,35	020
22	1	6	0,4	0,25	25
23	8	8	0,25	0,35	30
24	7	7	0,1	0,4	35
25	6	6	0,2	0,35	40
26	5	5	0,3	0,25	45
27	4	4	0,4	0,15	50
28	3	3	0,15	0,2	55
29	2	2	0,25	0,3	60
30	1	1	0,35	0,1	30

Сравнить результаты, полученные опытным путем, с вычисленными по уравнениям равновесия.

Отчет о работе. 1. номер варианта задания (по табл.2).

Расчетная схема балки. Данные: ;;;;.

2. Вычисление реакции опор по уравнениям (1). Проверка (см. табл.1, п.7). Полная величина реакции неподвижной опоры

,

где - численное значение горизонтальной и вертикальной составляющих реакции. Угол наклона

; .

3. Опытное определение реакций опор:

Контрольные вопросы:

1.      Сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил?

2.      Укажите, какие составляющие реакции опор балок возникают в подвижной, неподвижной опорах и жесткой заделке.

3.      Какую точку целесообразно принять за центр моментов (см.рис.4) при определении реакции опоры А?

Лабораторная работа №2

«Определение коэффициента трения».

Цель урока: научить учащихся вычислять на опыте коэффициент трения скольжения.

Оборудование: динамометр, набор грузов, деревянный брусок, деревянная линейка.

Экспериментальное определение коэффициента трения

1. Определяем силу тяжести бруска

 

1. Положив брусок на линейку, прикрепив к нему динамометр, тянем динамометр равномерно. Определяем силу трения.

1. Опыт проделываем 5 раз. Дополнительно добавляем грузы.

 

1. Вычисляем коэффициент трения.

 

1. Результаты опытов записываем в таблицу:

 

№ опыта	Сила тяжести N, Н	Сила трения , Н	Коэффициент трения, µ	Среднее значение, µ

 

 

 

 

 

 

1. Построить график зависимости силы трения от силы нормального давления.

, H

 

 

N, H

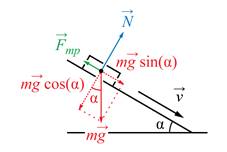
Дополнительное задание. Определение коэффициента трения вторым способом.

1. Устанавливаем линейку под таким углом, чтобы брусок скатывался равномерно.
2. Определив угол наклона α, вычисляем коэффициент трения по формуле:

 

1. Контрольные вопросы:

 

1. Что является причиной трения скольжения?

 

1. От каких факторов зависит сила трения скольжения?

 

1. Направление силы трения?

 

1. Как можно измерить силу трения?

 

4. Подведение итогов

Лабораторная работа №3

«Определение τ_nr при кручении».

Цель работы: Экспериментальным путем проверить закон Гука при кручении, определить предел прочности материала при кручении и выявить характер разрушения образца.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ

При кручении бруса круглого поперечного сечения в плоскостях, перпендикулярных к его продольной оси, и в плоскостях, совпадающих с этой осью, возникают только касательные напряжения; в плоскостях, расположенных под углом 45⁰ к оси бруса – только нормальные напряжения (главные).

Нормальные и касательные напряжения по величине не равны между собой, поэтому разрушение образца при кручении может произойти от сдвига или от отрыва. Так как сопротивление сдвигу или отрыву у различных материалов не одинаково, разрушение образцов при испытании на кручение будет происходить различно.

Оборудование и образцы

На кручение испытывают образцы цилиндрической и плоской формы, изготовленные в соответствии с требованиями ГОСТ 3565-58. Выбор размеров образцов зависит от величины предельного момента испытательной машины.

Для испытаний на кручение применяют специальные машины типа КМ-5 или К-50.

К данной лабораторной работе применяют машину КМ-50-1, предназначенную для испытания образцов из металла на кручение с наибольшим крутящим моментом 50 кгс∙м. На машине можно производить испытания образцов из других материалов (пластмасс, древесины и т.д.) в пределах ее конструктивных и технических возможностей.

Машина КМ-50-1 относится к типу испытательных машин с механическим нагружением вертикально расположенного образца и рычажно-маятниковым моментоизмерителем. Принцип действия машины заключается в следующем:

Образец, зажатый в захватах, подвергается кручению при помощи механизма провода. Момент, приложенный к нижнему захвату, передается через механизм нагружения маятнику, который отклоняясь, приводит в движение стрелку, показывающую величину крутящего момента на шкале силоизмерителя.

ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ

1.      В журнале испытаний записать тип машины.

2.      Измерить диаметры и расчетные длины образцов.

3.      Подготовить к работе диаграммный аппарат.

4.      Закрепить в захватах машины стальной образец, проследить за надежностью крепления головки образца в захватах, чтобы не было проскальзывания.

5.      Включив электродвигатель, довести образец до разрушения. Разрушение происходит без образования шейки и бесшумно.

6.      По шкалам зафиксировать наибольший момент Мпч и величину угла закручивания.

7.      Вынуть части образца и рассмотреть место поломки. Определить характер разрушения.

8.      Для чугунного и деревянного образца испытания проводятся в том же порядке, что и для стального образца.

9.      Вычислить условный предел прочности для образца при кручении:

а) стального образца

б) для деревянного образца

где М_ny – разрушающий момент; W_ny – полярный момент сопротивления, вычисленный по диаметру образца до испытания.

10.  По характеру поломки образца определить вид разрушения (имел ли место при разрушении сдвиг или отрыв частиц материала), т.е. выявить, какие напряжения для данного материала наиболее опасны.

11.  По величине угла закручивания, при котором произошло разрушение образца, определить пластичность материала.

СОСТАВЛЕНИЕ ОТЧЕТА

Отчет о проделанной работе должен содержать: схему испытательной машины, эскизы образцов до и после испытания, вычисления условных пределов прочности, построение диаграммы кручения, выводы о свойствах материалов, сделанных по характеру излома образцов.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.      Какие напряжение возникают в точках образца при кручении: в плоскостях, перпендикулярных к оси; в плоскостях, расположенных под углом 45⁰ к оси стержня?

2.      Как по характеру разрушения образца определить, какой вид напряжений наиболее опасен для данного материала?

3.      Что можно сказать о свойствах материала, если разрушение образца произошло по плоскости, расположенной под углом 45⁰ к его оси?

4.      Чем отличаются начальные участки диаграмм кручения стального и деревянного образца?

5.      При испытании установлено, что один образец разрушился при угле закручивания 60⁰, а другой – при угле 500⁰. Сравнить прочность и пластичность материалов.

 

Лабораторная работа №4

«Определение прогибов балки»

Цель работы. Экспериментальное определение прогибов и углов поворота сечений балки и сравнение их с результатами теоретических расчетов.

1. Краткие теоретические сведения.

При прямом поперечном изгибе ось балки искривляется. При малых деформациях допускают, что поперечные сечения балки перемещаются перпендикулярно первоначальной прямой оси балки и одновременно поворачиваются, оставаясь плоскими (согласно гипотезе Бернулли). Перемещения центра тяжести сечения δ в направлении перпендикулярном оси балки называются прогибом балки. Угол θ, на который поворачивается сечение по отношению к своему первоначальному положению, называется углом поворота сечения.

Для определения искомых перемещений используется энергетический метод Мора (интеграл Мора):

где  – изгибающий момент от заданной нагрузки;

–изгибающий момент от единичной нагрузки;

–изгибная жесткость балки.

Для вычисления прогиба в произвольной точке балки с помощью приведенной выше формулы необходимо выполнить последовательно следующие операции:

·         составить уравнения изгибающих моментов  от заданной нагрузки для каждого участка балки;

·         рассматриваемой балке приложить силу, равную единице, в той точке, где определяется перемещение. Единичная сила прикладывается в предполагаемом направлении этого перемещения;

·         составить уравнения изгибающих моментов  от единичной силы для каждого участка балки;

·         вычислить сумму интегралов от произведения обоих моментов  и ,деленного на жесткость поперечного сечения балки .

·         приложить единичный сосредоточенный момент к рассматриваемой балке, составить уравнение изгибающих моментови вычислить угол поворота θ поперечного сечения.

Вычисление интеграла Мора выполняется графоаналитическим способом Верещагина, применение которого допустимо при следующих условиях:

·         на рассматриваемом участке изгибная жесткость балки постоянна, т. е. ;

·         на этом участке одна из эпюр (или )имеет прямолинейное очертание.

По способу (правилу) Верещагина операция интегрирования заменяется перемножением площади одной из эпюр на ординату второй эпюры (обязательно линейной) под центром тяжести первой. В этом случае:

где - площадь одной из эпюр изгибающих моментов;

- ордината линейной эпюры изгибающих моментов,

под центром тяжести другой эпюры.

2. Применяемая установка и приборы.

Сравнительно гибкая балка 1 прямоугольного сечения опирается на две опоры, укрепленные на неподвижной станине. В сечениях В и С с балкой жестко соединены стержни 2 и 3. Между осью балки и осями стержней угол прямой. С помощью стрелочных индикаторов 6 и 7, касающихся своими штифтами концов стержней 2 и 3, определяются угловые перемещения сечений В и С балки. Индикатор 5, соединенный с балкой, позволяет определить линейные перемещения сечения К или прогиб. Индикаторы обычно имеют цену деления 0,01 мм и пределы измерений от 0 до 10 мм.

Нагружение балки осуществляется приложением одного, двух или более сосредоточенных грузов, прикладываемых в сечении К.

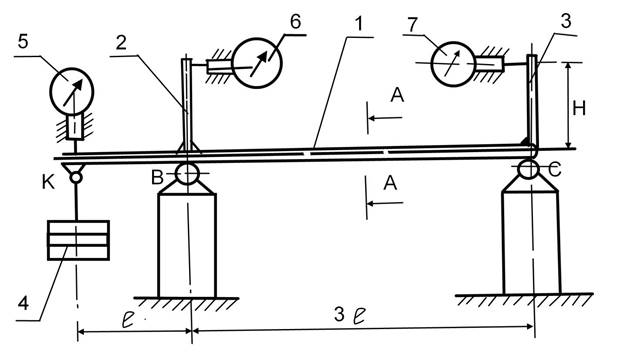
Рис. 1. Схема экспериментальной установки:

1 – балка; 2, 3 – стержни; 4 – груз; 5, 6, 7 – индикаторы часового типа; В и С – шарнирные опоры балки.

Размеры установки: l = 150 мм; H = 70 мм.

Размеры сечения: b = 30 мм; h = 4 мм.

Модуль упругости материала балки E = 2∙10⁵МПа.

Осевой момент инерции поперечного сечения балки

=(мм⁴ или м⁴).

3.Теоретическое определение перемещений сечений балки

Для определения прогиба балки в сечении К необходимо сначала на рис. 2 построить эпюру изгибающих моментов от силы F. Затем в сечении К балки, освобожденной от заданной нагрузки, необходимо приложить силу, равную единице и на том же рисунке построить эпюру изгибающих моментов от единичной силы .

Для вычисления углов поворота сечений В и С к балке, освобожденной от заданной нагрузки, в данных сечениях прикладываются единичные моменты и строятся эпюры единичных изгибающих моментов и.

Затем для построенных эпюр определяются величины ии по формуле (2) находится прогиб сечения балкиК и углы поворота сечений В и С.

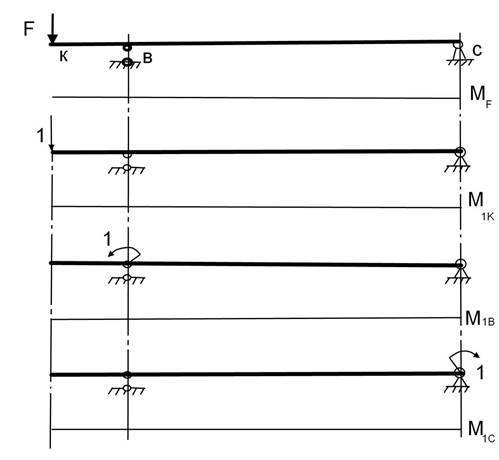
Рис. 2 Расчетные эпюры изгибающих моментов от заданной и

единичной нагрузок при определении прогиба и углов поворотаθ сечений балки

4. Порядок выполнения работы

·         Ознакомиться с установкой.

·         Производить нагружение образца последовательно силой 10 Н, 20 Н и 30 Н путем подвешивания грузов от 1кг до 3 кг в сечении К. Т. е. нагрузку увеличиваеть равными ступенями, величина каждой ступени нагружения ∆F= 10Н.

·         Фиксировать показания индикаторов ∆n_K, ∆n_B и ∆n_C на каждой ступени нагружения, подсчитывать разность показаний индикаторов ∆n_i и определять среднее значение приращения показаний каждого индикатора.

·         Определить опытное значение вертикального перемещения сечения К по формуле: (мм),

где k_D – цена деления индикатора (k_D= 0,01 мм/дел);

–среднее значение приращения показаний индикатора 5,

установленного в сечении К балки (см. рис. 1).

·         Вычислить опытные значения углов поворота сечений В и С (ввиду малости углов, находятся как тангенсы углов поворота этих сечений):

(рад), (рад),

где H - длина стержня (см. рис. 1);

и – средние значения приращений показаний

индикаторов 6 и 7, установленных в сечениях В и С.

·         Вычислить теоретические значения прогиба в сечении К и углов поворота сечений В и С.

·         Сравнить действительные прогибы и углы поворота сечений с перемещениями, рассчитанными с применением интегралов Мора по правилу Верещагина. Для этого вычислить расхождение между ними в процентах к расчетным величинам.

·         Составить отчет по данной лабораторной работе.

5. Результаты эксперимента

Нагрузка F	Приращение нагрузки ∆F	Показания и приращение показаний индикатора
		nK	∆ nK	nB	∆ nB	nC	∆ nC
0
10
20
30
Среднее	приращение на одну ступень нагрузки
показаний

Вертикальное перемещение сечения К: 

Углы поворота сечений В и С:

6. Сравнение результатов расчета с экспериментальными данными

Для сравнения величин линейных и угловых перемещений, полученных в опытах и расчетным путем, рассчитывается расхождение между ними  в процентах к расчетным значениям:

 

 

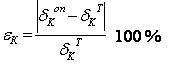
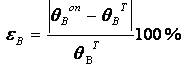
Перечень рекомендуемой основной и дополнительной литературы, Интернет–ресурсов, необходимых для освоения дисциплины

Основные источники:

1.         Кривошапко, С. Н. Сопротивление материалов. Практикум : учебное пособие для СПО / С. Н. Кривошапко, В. А. Копнов. – 4–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 353 с. (ЭБС Юрайт).

2.         Асадулина, Е. Ю. Сопротивление материалов. Конспект лекций : учебное пособие для СПО / Е. Ю. Асадулина. – 2–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 254 с. (ЭБС Юрайт).

3.         Техническая механика : учебник / Г.Г. Сафонова, Т.Ю. Артюховская, Д.А. Ермаков. – М. : ИНФРА-М, 2017. — 320 с. (ЭБС Знаниум).

Дополнительные источники:

1.         Родионов, В. Н. Физика : учебное пособие для СПО / В. Н. Родионов. – 2–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 295 с. (ЭБС Юрайт).

2.         Физика : учебник / А.А. Пинский, Г.Ю. Граковский ; под общ. ред. Ю.И. Дика, Н.С. Пурышевой. — 4-е изд., испр. — М. : ФОРУМ : ИНФРА-М, 2017. — 560 с. (ЭБС Знаниум).

3.         Горлач, В. В. Физика : учебное пособие для СПО / В. В. Горлач.– М. : Издательство Юрайт, 2017. – 175 с. (ЭБС Юрайт).

Интернет–ресурсы:

1.         ЭБС Юрайт https://www.biblio–online.ru/

2.         ЭБС Знаниум https://www.znanium.com

3.         ЭБС Лань https://e.lanbook.com/

4.         ЭБС Консультант студента www.studentlibrary.ru/

5.         Естественнонаучный образовательный портал: http://en.edu.ru

6.         Министерство образования Российской Федерации: http://www.ed.gov.ru

7.         Российский общеобразовательный портал: http://www.school.edu.ru

 

Скачано с www.znanio.ru