МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное учреждение высшего образования «Южный федеральный университет»

Институт математики, механики и компьютерных наук  им. И.И. Воровича

Кафедра теории и методики математического образования 

Уткина Мария Юрьевна

МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ 

РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ 

С ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА БАКАЛАВРА

По направлению 050100 Педагогическое образование

Профиль подготовки Математика

Научный руководитель -

к.п.н., доц. Михайлова Ирина Алексеевна

Ростов-на-Дону 2016 г.

Содержание

        Введение……………………………………………………………….     3

I.      Теоретические основы обучения учащихся решению текстовых  

задач……………….……………………………………………………. 5

1.1. История использования текстовых задач в процессе обучения…….. 5

1.2. Различные подходы к определению понятий «задача» и «текстовая       

задача»……..…………………………………………………..………... 8

1.3. Функции решения текстовых задач………………………………….          10

1.4. Классификация текстовых задач……………………………………… 12

1.5. Методы решения текстовых задач……………………………………. 15

1.6. Этапы решения задач…………………………………………………..        17

II.  Методика обучения учащихся решению текстовых задач с эко- номическим содержанием……………………………………….     22

2.1. Задачи с экономическим содержанием в обучении математике ……        22

2.2. Методические особенности обучения учащихся решению задач,     содержащих сведения об оплате труда ………………………………         25

2.3. Методические особенности обучения учащихся решению экономи- ческих задач с помощью линейных, квадратичных функций и нера-

              венств ……………………………………………………………..               32

2.4. Анализ педагогического опыта обучения учащихся решению тек- стовых задач с экономическим содержанием ………………………    39

        Заключение ……………………………………………………………      45

        Список литературы ………………………………………………….       47

        Приложение 1. Классификация текстовых задач ……………………      50

        Приложение 2. Решение одной задачи различными методами …….       51

        Приложение 3. Словарь основных экономических понятий ……….       54

Введение

Переход России к рыночным отношениям привел к стремительной «экономизации» нашего общества. До недавнего времени никто, кроме специалистов в экономике не использовали в лексиконе такие термины, как предпринимательство, бизнес, реструктуризация, рефинансирование и т. д.

Сегодня проблемы стремительно развивающегося рынка влияют на всех нас. Они уверенно демонстрируют нам, что в основе нашей жизни лежат экономические отношения, ядром которой является предпринимательство. Эти изменения произошли менее чем за 10 лет, вызвав сегодня в нашем обществе естественный интерес к экономическим знаниям и законам экономики.

Сегодня как взрослые, так и учащиеся ставят перед обществом вопрос: «От чего зависит сегодняшний уровень цен? Почему они только растут? Почему государство не может их установить на таком низком уровне, чтобы книг, игрушек, продуктов питания и других товаров хватало на всех? Почему «тают» наши сбережения и как их спасти? Что хорошего или плохого в изменении курса доллара, о котором нам рассказывают по несколько раз в день? В чем смысл реструктуризации внешних долгов?» и т. д.

Быстрая экономизация российского общества требует овладения учащимися определенным набором экономических знаний уже на школьной скамье, а перестройка математического образования будет рассматриваться как новая содержательно-методическая линия - экономическая, и позволит сконструировать «экономическую составляющую» школьного курса математики.

Под экономической составляющей школьного курса математики понимается совокупность простых экономических понятий, их свойства и специально сконструированный набор задач, которые имеют реальное экономическое содержание, которые могут быть решены на основе математических знаний, соответствующих классов, начиная с 5 по 11 классы [21].

В связи с вышесказанным тему исследования можно считать актуальной.

Охарактеризуем методологический аппарат исследования.

Объект исследования – текстовые задачи экономического содержания в школьном курсе математики. 

Предмет исследования - методика обучения учащихся решению текстовых задач с экономическим содержанием.

Цель исследования - описать методику обучения учащихся решению текстовых задач с экономическим содержанием.

Задачи исследования:

1.                 Изучить психолого-педагогическую, математическую и методическую литературу по теме исследования. 

2.                 Охарактеризовать теоретические основы обучения учащихся решению текстовых задач.

3.                 Описать методические особенности обучения учащихся решению задач с экономическим содержанием.  

4.                 Провести анализ педагогического опыта обучения учащихся решению задач с экономическим содержанием. 

Охарактеризуем структуру работы.  Выпускная квалификационная работа состоит из введения, двух глав, заключения, списка литературы и приложений. В приложениях представлены: 1) классификация текстовых задач; 2) решение одной задачи различными методами; 3) словарь основных экономических понятий.

          I.         Теоретические основы обучения учащихся решению текстовых

задач

                1.1     История использования текстовых задач в процессе обучения

В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место. Применение текстовых задач идет от глиняных табличек Древнего Вавилона и других древних письменных источников. Долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями.

В литературе [11] выделяются основные причины пристального интереса к такого рода задачам:

1)    Первая причина заключается в том, что исторически долгое время целью обучения детей арифметике было освоение ими определенным набором вычислительных умений, связанных с практическими расчетами. При этом основная линия числа - еще не была разработана, а обучение вычислениям велось через задачи. В «Арифметике» Л. Ф. Магницкого, например, дроби рассматривались как именованные числа (не просто (), а ) рубля, пуда и т. п.), а действия с дробями изучались в процессе решения задач [12]. Эта традиция сохранялась довольно долго. Даже много позже встречались задачи с неправдоподобными числовыми данными, например: «Заяц в 1,35 часа пробегает 14,13855 км.», которые были вызваны к жизни не потребностями практики, а потребностями обучения вычислениям.

2)    Вторая причина заключается в использовании старинного способа передачи математических знаний, приемов и рассуждений с помощью текстовых задач. С помощью задач научились формировать важные общеучебные умения, связанные с анализом текста, выделением условий задачи и главного вопроса, составлением плана решения, поиском условий, из которых можно получить ответ на главный вопрос, проверкой полученного результата. Так же важную роль играло приучение школьников к переводу текста на язык арифметических действий, уравнений, графических образов. Использование арифметических способов решения задач способствовало общему развитию учащихся, развитию не только логического, но и образного мышления, а это повышало эффективность обучения математике и смежных дисциплин.

К середине XX века в СССР сложилась развитая типология задач, включавшая задачи на части, на нахождение двух чисел по их сумме и разности, по их отношению и сумме (разности), на дроби, на проценты, на совместную работу и пр. Методика обучения решению задач была разработана достаточно хорошо, но ее реализация на практике не была свободна от недостатков. Критики этой методики обоснованно отмечали, что учителя, стремясь ускорить процесс обучения, разучивали с учащимися способы решения типовых задач, как бы следуя своим давним предшественникам. Они считали также, что в процессе обучения решению текстовых задач школьников учили способам действий, которые не применяются или почти не применяются в жизни. 

Вот как описывал И. В. Арнольд практику обучения решению задач, сложившуюся в нашей стране к середине 40-х годов: «Учеников - в том или ином порядке - знакомят с соответствующими «типами» задач, причем обучение решению задач, сплошь и рядом сводится к «натаскиванию», к пассивному запоминанию учениками небольшого количества стандартных примеров решения и узнаванию по тем или иным признакам, какой из них надо применить в том или ином случае. Количество задач, которые ученики решают действительно самостоятельно, с тем напряжением мысли, которое и должно являться источником полезности процесса решения задачи, ничтожно. В итоге - полная беспомощность и неспособность ориентироваться в самых простых арифметических ситуациях, при решении чисто практических задач» [1, с.14].

Так или иначе, но в середине XX в. в СССР возобладал узко практический подход к использованию текстовых задач. Тогда считалось, что обучать детей нужно с учетом возможностей применения изученных способов действий на практике или в дальнейшем обучении. Отражение споров тех лет о текстовых задачах находим у Ю.М. Колягина: «Заметим, что старые традиции весьма живучи и способны к такой внешней трансформации, что иногда их трудно распознать. Отрицательная обучающая роль типовых арифметических задач признана всеми. Однако не уготована ли та же участь задачам на составление уравнения?» [11, с. 58]. Волнение по поводу задач, которые решаются с помощью уравнений, оказались преждевременными, но роль алгебраического способа решения задач в учебном процессе в последующие годы была явно завышена, именно потому, что из школьной практики были удалены арифметические способы их решения. 

 Традиционные для российской школы арифметические способы решения задач считались устаревшими и перешли к раннему использованию уравнений. Такой подход казался более современным и научным.

Есть еще один момент, который нельзя избежать, когда мы говорим о решении задачи. Обучение и развитие ребенка во многом напоминают этапы развития человечества, поэтому использование старинных задач и арифметическое множество их решений обеспечивает мотивацию учения, развивает творческий потенциал. Кроме того, разнообразные способы решения помогают пробудить воображение детей, помочь организовать поиск решения каждый раз новым способом, что создает благоприятный эмоциональный фон для обучения.

В данном параграфе мы  рассмотрели историю использования текстовых задач. Выделили основные причины пристального интереса к такого рода задачам.  Из выше изложенного можно сделать вывод что, применение текстовых задач  зарождается еще в древности, а методика обучения решению задач была разработана достаточно хорошо лишь в середине XX века.

Хотя ее реализация на практике имела множество недостатков. Далее рассмотрим различные подходы к понятию текстовая задача.

1.2. Различные подходы к определению понятий задача и текстовая задача

Существуют разные подходы к определению понятий «задача» и «тек-

стовая задача». 

По определению Г.А. Балла, в самом общем виде задача - это система, обязательными компонентами которой являются: а) предмет задачи, находящийся в исходном состоянии (исходный предмет задачи); б) модель требуемого состояния предмета задачи (требование задачи) [4].

Л.М. Фридман и Е.Н. Турецкий понятие «задача» трактуют как «требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче» [27, с.6]. 

Л. Л. Гурова обращает главное внимание на объект мыслительных усилий человека, решающего задачу: «Задача - объект мыслительной деятельности, содержащий требование некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными ее элементами» [23,с. 101].

Подход к понятию «текстовая задача» неоднозначен. Согласно первому подходу если в задаче хотя бы один объект реальный, то она называется текстовой (практической, житейской, сюжетной). В соответствии со вторым подходом под текстовой задачей понимают задачу, условие и требование которой представлены связным текстом, состоящим из повествовательных и вопросительных предложений. Если в текстовой задаче описаны геометрические или физические объекты, математические отношения или физические процессы, то получаем геометрическую или физическую задачу. 

Под текстовыми задачами понимаются математические задачи, в которых входная информация содержит не только математические данные, но еще и некоторый сюжет (фабулу задачи) [29].

По определению Стойловой Л.М. текстовая задача – это задача, сформулированная на естественном языке; в ней обычно описывается количественная сторона каких-то явлений, событий; она представляет собой задачу на разыскание искомого и сводится к вычислению неизвестного значения некоторой величины [24].

Каждая текстовая задача есть модель проблемной или познавательной ситуации, в которой рассматривается некоторый объект (предмет, явление, процесс). Каждый объект описан в задаче. Своеобразие описания объектов задачи проявляется в том, что в ней описывается лишь количественная сторона объекта [2].

Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между его компонентами ли определить вид этого описания [4].

В качестве необходимых элементов текстовой задачи можно выделить следующие: 

•              числовые данные, характеризующие мощность множеств, значения величин, о которых идет речь в задаче, или их отношения, а также просто являющиеся отвлеченными числа; 

•              словесные пояснения зависимости, имеющейся между данными числами и между данными и искомыми, которая может быть представлена в виде некоторого сюжета; 

•              вопрос задачи, для ответа на который требуется выполнить решение. 

Текст любой задачи состоит из условия и требования. 

Условие задачи - это описание ситуации особого типа. Анализируя условия, можно заметить, что каждое из них состоит из одного или нескольких объектов и некоторой их характеристики. В условии математической задачи описывается ситуация, в которой неизвестна какая-либо характеристика (или характеристики) того или иного объекта (или объектов) [2].

Требование задачи состоит в том, чтобы описать с необходимой полнотой так называемые искомые характеристики, т. е. все или некоторые неизвестные характеристики. Для этого следует использовать связи между известными и неизвестными характеристиками. Количество известных и неизвестных характеристик в задаче может быть различным [2]. 

Требование математической задачи может выражаться как вопросительным предложением, так и повествовательным с глаголом в повелительном наклонении. Предложение, которым чаще всего завершается текст задачи, может, кроме требования, содержать в себе и часть условия.

Итак, мы охарактеризовали различные подходы к определению понятий «задача» и «текстовая задача». В различных определениях эти понятия рассматриваются под различными углами зрения и соответственно наполняются различным содержанием.  Каждое определение построено для достижения определенных целей. В конкретных ситуациях договариваются в рамках какого определения происходит рассмотрение данных понятий. 

1.3. Функции решения текстовых задач

Вопросу определения функций задач в обучении уделяется много внимания в методической литературе. В педагогической практике принято разделять задачи с дидактическими, познавательными и развивающими функциями.

В методике обучения решению задач выделяют четыре их основных функции – обучающая, воспитывающая, развивающая и контролирующая.

1.     Обучающая функция задач направлена на формирование у учащихся системы математических знаний, умений и навыков в процессе их усвоения.

2.     Воспитывающая функция задач направлена на воспитание у учащихся интереса к предмету, навыков учебного труда.

3.     Развивающая функция задач направлена на развитие мышления учащихся. На формирование у них приемов умственной деятельности.

4.     Контролирующая функция задач направлена на определение уровня усвоения учащимися учебного материала, способности их к самостоятельному изучению школьного курса математики, уровня развития и сформированности познавательных интересов школьников.

Рассмотрим  дидактические функции задач, выделяемые Л.М. Фридманом [26].

1.     Вводно-мотивационная функция. Предварение изучения математической теории постановкой задач представляет хорошие возможности для использования на уроках математики элементов проблемного обучения. Задачи проблемного характера для достижения целей обучения математике весьма значимы. Их использование обеспечивает более осознанное овладение математической теорией, учит школьников самостоятельному выполнению учебных заданий, приемам поиска, исследования и доказательства, основным мыслительным операциям, выделению существенных свойств математических объектов. Для создания проблемных ситуаций целесообразно использовать наряду с другими и задачи с практическим содержанием. 

2.     Иллюстративная и конкретизирующая функция. В качестве иллюстраций и конкретизаций различных математических понятий целесообразно использовать текстовые задачи, в которых раскрываются особенности изучаемых понятий. Примеры из окружающей действительности позволяют раскрывать перед учащимися практическую значимость математики. Эти примеры должны быть простыми, убедительными, доступными пониманию школьников. Понятие линейной функции представляется возможным иллюстрировать многочисленными примерами из физики, химии, повседневной жизни. 

3.     Функция формирования математических и общеучебных умений и навыков. В школьном курсе математики учащиеся приобретают ряд специальных и общеучебных математических умений и навыков. Все эти умения и навыки формируются не только при решении специальных примеров, но, и главным образом, в процессе решения простейших задач. Различны формы использования текстовых задач для закрепления и углубления знаний учащихся по математике. Эти задачи могут быть применены и в работе со всем классом, и для индивидуальной работы с отдельными учениками. 

4.     Функция воспитания характера и воли. Решение текстовых задач, особенно сложных, требует от учащихся настойчивости, последовательности и аргументации рассуждений, сосредоточенности волевых качеств. Целесообразнее дать учащимся достаточное время для решения каждой задачи, нежели гнаться за количеством решенных задач. 

5.     Функция развития творческого мышления и воображения. В математике разработаны многочисленные так называемые «задачи на смекалку и сообразительность», требующие для решения каких-то особых приемов. Такие задачи можно давать учащимся для самостоятельного решения на дом на длительный срок.

Таким образом,  исследование функций текстовых задач позволяет сделать вывод о том, что функции задач в обучении взаимосвязаны, однако в каждом конкретном случае выделяется и реализуется ведущая функция задачи. 

1.4. Классификация текстовых задач

Существует множество различных подходов к классификации текстовых задач. Рассмотрим некоторые из них. 

Л.М. Фридман, Е.Н. Турецкий [27] предлагают классифицировать задачи по характеру объекта, отношению к теории и характеру требований.

Задачи, решаемые в школе, различаются в первую очередь характером своих объектов. В одних задачах объектами являются реальные предметы, в других - все объекты математические (числа, геометрические фигуры, функции и т.д.). Первые задачи, в которых хотя бы один объект есть реальный предмет, называют практическими (житейскими, текстовыми, сюжетными); вторые, все объекты которых математические - математическими задачами.

Математические задачи, для решения которых в школьном курсе математики имеются готовые правила (в любой форме) или эти правила следуют из каких-либо определений или теорем, определяющих программу решения этих задач в виде последовательности шагов, называются стандартными. При этом предполагается, что для выполнения отдельных шагов решения стандартных задач в курсе математики также имеются вполне определенные правила.

Нестандартные задачи - это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точный алгоритм их решения. 

По характеру требования Л.М. Фридман и Е.Н. Турецкий [27] все задачи делят на три основных класса.

Задачи на нахождение искомого. В задачах этого класса требование состоит в том, чтобы найти, разыскать, распознать какое-то искомое. При этом искомым могут быть величина, отношения, какой-либо объект, предмет, его положение или форма и т. д. 

Примерами задач этого класса являются задачи на вычисление различных выражений, значений функций, задачи на установление характера функции и т. д. Задачи на решение различных уравнений, систем уравнений, неравенств и их систем также принадлежат к этому классу задач, ибо в каждой из них нужно найти значения некоторых переменных, удовлетворяющих определенным условиям. Этот класс задач многочисленный и разнообразный. 

Задачи на доказательство или объяснение. В задачах этого класса требование состоит в том, чтобы убедиться в справедливости некоторого утверждения, или проверить верность или ложность этого утверждения, или, наконец, объяснить, почему имеет место то или иное явление, тот или иной факт. Все задачи, требование которых начинается со слов «доказать», «проверить» или содержащие вопрос «Почему?», относятся к этому классу задач. 

Задачи на преобразование или построение. К этому классу относятся задачи, в которых требуется преобразовать какое-либо выражение, упростить его, представить в другом виде, построить что-либо (например, геометрическую фигуру или выражение), удовлетворяющее указанным условиям. Класс этих задач также весьма обширен. Характерной особенностью задач этого класса является то, что в каждой из них заданы какие-то объекты (элементы, выражения), из которых требуется создать, построить, сконструировать другой какой-то объект с заранее известными свойствами.

 Т.Е. Демидова и А.П. Тонких [9] предлагают классифицировать задачи по их типу и виду, понимая под типом задачи классификацию по содержанию: задачи на движение, задачи на части, задачи на проценты и т.п. Внутри каждого типа в зависимости от логической структуры задачи различают виды задач. 

Так же задачи можно классифицировать таким образом [23]:

1)    по содержанию: 

                                      экономического содержания:

-    купля – продажа;

-    оптимальный выбор;  спрос – предложение;  бизнес.

•              физического содержания. 

•              прямая пропорциональная зависимость:  движение (в том числе движение по суше и реке);

 работа (в том числе и совместная).

                                      задачи на смеси, сплавы, растворы.

2)    по методу решения: 

•              арифметические;

•              алгебраические (составление уравнений, неравенств и их систем);

•              геометрические (через использование геометрических фи-

гур и их свойств);

•              комбинированные.

3)    по специфике языка: 

•              текстовые (условие представлено на естественном языке);

•              сюжетные (присутствует фабула);         абстрактные (предметные).

Всякая типология задач является условной и зависит от многих обстоятельств. Так, например, одну и ту же задачу можно решить и арифметическим, и алгебраическим, и геометрическим методами. А отнесение задачи к тому или иному виду по степени проблемности зависит от того, кто решает задачу. Несмотря на это, различные типологии позволяют учителю более осознанно подходить к отбору задач в зависимости от целей обучения [16].

Итак, существует достаточно большое количество различных классификаций. Отразим их многообразие в схеме, представленной в приложении 1.

1.5. Методы решения текстовых задач

Решить математическую задачу - это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется в задаче, - ее ответ [27]. 

Под решением задачи Г.А. Балл понимает воздействие на предмет задачи, обусловливающее ее переход из исходного состояния в требуемое. Решенная задача, т.е. задача, предмет которой приведен в требуемое состояние, перестает быть задачей [4].   

Существуют различные методы решения текстовых задач: арифметический, алгебраический, графический, геометрический.

1.     Арифметический метод. Решить задачу арифметическим методом - значит найти ответ на требование задачи посредством выполнения арифметических действий над значениями указанными в задаче [19]. 

Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи.

В методике преподавания отличают типы задач, для которых наиболее целесообразным является арифметический метод решения: 

•   все простые задачи, решаемые одним из четырех арифметических действий; 

•   задачи на нахождение дроби (части) числа и числа по известному значению его дроби (части), отношения одного числа и другого и соответствующие им задачи на проценты. 

В задачах указанных типов нет необходимости вводить переменную для нахождения искомого. При арифметическом методе формы записи решения могут быть:

-            вопрос с последующим действием; 

-            действие с последующим объяснением;          запись решения с предшествующим пояснением;           числовое решение без текста.

2.     Алгебраический метод. Решить задачу алгебраическим методом - значит найти ответ на требование задачи, составив и решив уравнение (неравенство) или систему уравнений (неравенств) [24].

Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.

При обучении решению алгебраическим методом целесообразно требовать от школьников проговаривать мотивировки составления уравнений. Желательно одну и ту же задачу решать, составляя различные уравнения при выборе за неизвестное различные величины.

3.     Геометрический метод. Решить задачу геометрическим способом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.   

В геометрическом методе предусматривается использование геометрических объектов и их свойств, при решении задачи в рамках математической модели (метод сравнения длин отрезков (отрезочные диаграммы), метод подобия, метод площадей (двумерные диаграммы)).

Основным преимуществом геометрического решения является наглядность, так как чертёж помогает глубже понять условие задачи.

4.     Графический метод. Л.М. Фридман [26] выделяет в отдельный метод решения текстовых задач - графический метод. Для которого достаточно знать только график прямой пропорциональности. При графическом решении задач удобнее пользоваться переменной системой, а именно иметь на одном и том же чертеже несколько различных систем координат для построения заданных в условии задачи зависимостей, причем каждая зависимость изображается в своей системе координат.

Следует отметить, что практически каждая задача в рамках выбранного метода допускает решение различными способами, т.е. решение с помощью различных моделей.  В качестве примера рассмотрим различные методы решения одной задачи (Приложение 2).

1.6. Этапы решения задач

Выделяются четыре этапа решения текстовой задачи [24]:

1                   этап. Анализ задачи. Основное назначение этапа - осмыслить ситуацию, описанную в задаче; выделить условия и требования, выделить все отношения между объектами задачи. Анализ задачи может проводиться по двум направлениям: 

•              предметно-содержательный анализ - это декодирование условия задачи в целом, воссоздание той реальной задачной ситуации, моделью которой является данная задача. Такой анализ обычно проводят устно, и создаваемая на основе этого анализа задачная ситуация образует у решающего мыслительный образ сюжета задачи. 

•              логико-семантический анализ - это анализ текста задачи для установления величин, их значений и соотношений между ними, заданных в тексте задачи, разбиения тем самым текста задачи на отдельные элементарные условия и требования. Таким образом, выявляется структура задачи.

Для оформления результатов анализа используются разного рода схематические записи задач.

Схематическая запись - это вспомогательная модель, помогающая перевести текст задачи со словесного языка в математический.

Схематическая запись может быть представлена в виде: 

•              схемы; 

•              таблицы; 

•              чертежа;

•              рисунка; 

•              ключевых слов. 

К выполнению чертежей предъявляются требования: они должны быть наглядными, четкими, соответствовать тексту задачи; на них должны быть отражены по возможности все данные, входящие в условие задачи; выделенные на них данные и искомые должны соответствовать условию задачи и общепринятым обозначениям. 

После построения вспомогательной модели необходимо проверить: 

•              все ли объекты задачи показаны на модели;

•              все ли отношения между объектами отражены; 

•              все ли числовые данные приведены;      есть ли требование.  

2                   этап. Поиск плана решения задачи. Назначение этапа - завершить установление связей между данными и искомыми величинами и указать последовательность использования этих связей (составить план решения). 

Поиск пути решения можно осуществлять от вопроса задачи к данным - аналитический путь, или от данных к вопросу - синтетический путь. 

Анализ в форме рассуждения от искомого к данным подразделяется на два вида восходящий и нисходящий.

Общая схема восходящего анализа заключается в следующем: пусть требуется доказать утверждение А. Подбираем такое утверждение В, из которого следует А. Затем отыскиваем утверждение С, из которого следует В, и т. д. до тех пор, пока находим путь решения задачи. 

Обычно восходящий анализ применяют совместно с синтезом. Используемый при этом метод называют аналитико-синтетическим или методом попеременного движения с двух сторон - от данных задачи к искомому и обратно. Сначала стараются получить ряд следствий из данных, а затем - такие утверждения, из которых следовало бы искомое. Далее опять возвращаются к данным и т. д. Особенности данного метода: 

•              при восходящем анализе не требуется обратимости рассуждений, так как возможность обратного перехода проверяется на каждом шаге поиска решения; 

•              применяя восходящий анализ, мы фактически пользуемся аналитико-синтетическим методом; 

•              общая схема восходящего анализа несколько отличается от формы, словесных рассуждений при его использовании. Учащиеся должны хорошо усвоить эту форму: «Чтобы доказать..., достаточно доказать...». На первых порах учащиеся обычно заменяют термин «достаточно» словом «надо». Разъясняем, что здесь более подходит термин «достаточно», поскольку мы можем подобрать несколько различных утверждений, для каждого из которых искомое является следствием; 

•              в общей схеме восходящего анализа (в отличие от нисходящего) не разъясняется, как получить утверждение, из котором следует искомое. Такое утверждение подыскивается, исходя из конкретных условий решаемой задачи. 

Сходство восходящего анализа с нисходящим заключается в том, что у них одна и та же форма анализа - рассуждения от искомом к данным. 

В.А. Далингeр [8] предлагает разбор задачи от ее вопроса к ее условию изобразить в виде схемы - «дерево рассуждений». Построение этого «дерева» называется анализом, а решение задачи по данной схеме - синтезом.

3                   этап. Осуществление плана решения задачи. Назначение этапа - найти ответ на требование задачи, выполнив все действия в соответствии с планом. Немаловажную роль играет запись решения. 

4                   этап. Проверка решения задачи. После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи, для этого производят проверку решения. 

Проверка решения текстовых задач может быть прямой или косвенной, в свою очередь, каждая из них может быть полной или неполной (частичной). Прямая полная проверка решения состоит в том, что мы убеждаемся в выполнении всех условий задачи при найденных значениях искомых. Неполная проверка состоит в том, что мы проверяем выполнение не всех условий, а лишь некоторых.

Косвенную проверку задачи можно произвести с помощью составления и решения обратной задачи. Обратная задача составляется путем обмена ролями одного из искомых с каким-либо из данных, т.е. найденное значение одного из искомых принимают за данное, а одно из данных считают искомым. Если в результате решения обратной задачи получают значение, совпадающее с выбранным данным, то это показывает, что проверка «сошлась».

Косвенную проверку решения задачи можно выполнить и с помощью решения этой же задачи каким-либо другим способом. 

Анализируя вышеизложенное можно сделать вывод, что для решения текстовых задач необходимо знать основные этапы решения и некоторые приемы их выполнения.   

II.      Методика обучения учащихся решению текстовых задач с экономическим содержанием

2.1. Задачи с экономическим содержанием в обучении математике

В настоящее время экспериментально доказано, что решение задач с экономическим содержанием способствует формированию экономических понятий и воспитанию мышления на базе выявления логических связей между этими понятиями на этапах формализации и интерпретации задач с практическим содержанием.

Под текстовой задачей с экономическим содержанием подразумеваем задачу, сформулированную в области экономики, решение которой требует использовании математического аппарата. [17]

При решении этих задач учащиеся замечают, что с ростом производительности труда растет и заработная плата, что производительность труда связана с себестоимостью выпускаемой продукции, т. е. с ростом производительности труда себестоимость снижается, и, наконец, на рост производительности труда влияют научные методы организации работ, применение новых технологических процессов, методов и приемов труда, т. е. устанавливают взаимосвязи экономических явлений.

Введение экономических знаний в содержание задач, решаемых математическими методами, как отмечает А.С. Симонов [22], преследует достижение двух целей. Первая из них состоит в том, чтобы продемонстрировать школьникам эффективность применения математических методов к решению реальных экономических задач и тем самым показать связь математики с окружающим миром и реальный смысл ее абстрактных конструкций. Вторая цель состоит в развитии экономического образа мышления - умения применять аппарат математики и экономики для анализа конкретных экономических явлений и процессов.

В процессе решения математических задач с экономическим содержанием возникает необходимость систематизации экономических понятий, вводимых в условия задач. Словарь основных экономических понятий представлен в приложении 3.

Систематизация этих понятий осуществляется следующим образом:

а) составляется условие задачи так, чтобы сущность вводимых экономи-

ческих понятий раскрывалась условием самой задачи;

б) проводится элементарный экономический анализ тех ситуаций, которые отражены в условии самой задачи.  Под экономическим анализом понимается, с одной стороны, выявление логических связей между экономическими понятиями, с другой – на базе анализа экономических явлений, описанных в условии задачи, определение взаимосвязей этих явлений. Это обстоятельство положено  в основу экономико-математического мышления учащихся.

Отметим, что главными факторами воспитания экономической грамотности учащихся являются:

а)  выяснение содержания экономических понятий и установление их

логических связей;

б)  умение проводить теоретический экономический анализ экономиче-

ских ситуаций;

в) умение проводить количественный экономико-математический ана-

лиз экономических явлений.

Эти основные положения лежат в основе установления трехуровневой системы задач в процессе обучения учащихся.

Рассмотрим эту систему уровней:

ü    первый уровень. Пропедевтика элементарных экономических знаний на базе конкретно рассматриваемых задач с экономическим содержанием. На этом уровне повторяются и углубляются «предшествующие», «сопутствующие», а также «предваряющие» экономические понятия и выявляются логические связи между ними;

ü    второй уровень. Формирование простейших навыков элементарного экономического анализа. На этом уровне решаются более сложные задачи в экономическом аспекте по результатам решения которых учащиеся должны выполнить элементарный экономический анализ, т.е. выявлять взаимосвязи экономических явлений, рассматриваемых в условиях задачи;

ü    третий уровень. Развитие у учащихся умения проводить элементарный количественный экономико-математический анализ. На этом уровне рассматривается система задач, содержание которых связано с необходимостью выполнения количественного элементарного экономического анализа конкретно рассматриваемых в задаче экономических факторов с целью определения прибыли, т.е. выявления рентабельности предприятия, цеха, участка и т.п.

Выделяют три этапа решения прикладных задач с экономическим содержанием [15]: 

1)    этап формализации. На этом этапе происходит переход от реальной экономической ситуации к адекватной экономикоматематической модели. Построение экономико-математической модели зависит, прежде всего, от структуры самой задачи, от взаимосвязей между компонентами, которые даны в условии задачи. Если зависимости между экономическими компонентами простые, то составление экономико-математической модели не вызывает у учащихся затруднений.

На этапе формализации для перехода от реальной экономической ситуации к построению адекватной экономикоматематической модели учащиеся должны выявить взаимосвязи между компонентами, которые приведены в условии задачи, уметь выразить их математическими символами, и чем сложнее условие задачи, тем сложнее взаимосвязи между компонентами, как в математическом, так и в экономическом плане. В результате повышается уровень математического развития и экономической грамотности учащихся. 

2)    этап решения математической модели. На этом этапе у учащихся развиваются: умения пользоваться математическим аппаратом, находить новые приемы решения этой модели, если известные им методы решения являются не совсем рациональными, и т.д., математические способности в теоретико-математическом аспекте. 

3)    этап интерпретации. На этом этапе у учащихся развиваются умения: проведения подробного анализа экономических явлений, описанных в условии задачи; выявления соответствия полученных результатов смыслу экономической задачи; оценки и осмысления значений данных экономических факторов для практической деятельности людей; нахождения путей улучшения экономических факторов, устранения недостатков.

В следующем параграфе мы продемонстрируем все вышесказанное на конкретных примерах задач с экономическим содержанием разных видов. 

2.2. Методические особенности обучения учащихся решению задач, содержащих сведения об оплате труда

Остановимся на методике обучения учащихся решению задач, содержащих сведения об оплате труда. Эти задачи требуют предварительного знакомства учащихся с определенной теорией. Так, например, они должны знать, что на предприятиях нашей страны применяются в основном три формы оплаты труда – повременная,  сдельная и договорная. С учетом премиальных при повременной оплате труда измерителем количества затраченного времени служит число часов или дней, отработанных рабочим, с учетом его квалификации. Повременная оплата труда подразделяется на почасовую, поденную и помесячную. Предварительно учащиеся знакомятся с такими понятиями, как норма времени, норма выработки, тарифная ставка, расценка. Даются пояснения к этим понятиям.

Нормой времени называется то количество времени, которое потребуется рабочему определенной профессии и квалификации на производство единицы продукции или выполнение единиц другой работы. Норма выработки означает количество изделий, произведенных рабочим в единицу рабочего времени.

Тарифная ставка определяет размер оплаты труда за единицу времени (час, день, месяц). Расценка выражает денежную стоимость в рублях или копейках единицы продукции или единицы работы. Зависимость между нормой выработки и нормой времени выражается следующей формулой:  , где Т_см – сменное время, Н_выр – норма выработки, Н_вр – норма

времени.

Учащимся сообщается, что почасовая оплата определяется умножением часовой тарифной ставки, которая соответствует тарифному разряду рабочего, на фактически отработанное время в часах.

Аналогично подсчитывается поденная зарплата, только вместо почасовой тарифной ставки берётся дневная, а время подсчитывается в днях. Помесячная зарплата определяется делением месячного оклада рабочего на количество рабочих часов или дней в данном месяце, а затем умножается на отработанное число часов, дней.

Приведем примеры решения такого типа задач. 

Пример 1. Месячная заработная плата рабочего 15400 руб. при условии, что он отработал 22 рабочих дня, Однако фактически отработанных дней было 19.

Вычислите какую заработную плату в этом месяце получит рабочий. 

Месячная зарплата рабочего составляет:  13300(руб.).

Пример 2. Слесарь пятого разряда, который работает по повременной оплате труда, в течение месяца имеет 23 рабочих дня. Тарифная ставка, соответствующая его разряду, равна 68,4 руб. Вычислите его месячную заработную плату. 

Месячная заработная плата составит: 23868,4 12586 (руб.).

Пример 3. Дневной заработок рабочего четвертого разряда составляет 406 руб., а количество рабочих дней равно 22. Вычислите его месячную заработную плату. 

Месячная зарплата равна 224068932 (руб.).

Все вышеприведенные примеры есть задачи первого уровня. Их решение должно предшествовать решению более сложных задач второго и третьего уровней. 

При сдельной оплате труда заработная плата рабочего зависит от количества произведенной продукции. На каждую единицу продукции устанавливается норма времени и расценка.

Учитель должен объяснить учащимся, что часто работа выполняется не одним рабочим, а бригадой, состоящей из нескольких человек, у которых разное количество отработанных часов и разная квалификация. Заработная плата каждого рабочего в этом случае определяется двумя методами.

 З^бр 

1.   Вычисляется по формуле: З_р  _Тбр _Т_р (1), где З_р – сдельный зара-

_

боток члена бригады; З_бр – сдельный заработок бригады; Т_бр – тарифный заработок бригады; Т_р– тарифный заработок одного рабочего.

 Збр 

2.   Вычисляется по формуле: З_р  _ _Кбр _К_р (2), где К_бр – общая сумма ко-

эффициентов – часов по бригаде в целом; К_р – количество коэффициентов – часов у отдельного рабочего.

Для удобства нахождения тарифных ставок, соответствующих данному разряду, вводится тарифная сетка. Тарифный коэффициент 1-го разряда всегда равен единице, тарифные коэффициенты последующих разрядов показывают, во сколько раз труд рабочего, имевшего высокий разряд, производительнее, и соответственно оплачивается выше по сравнению с трудом рабочего, имеющего первый разряд. Зная тарифный коэффициент любого разряда, можно путем умножения на тарифную ставку первого разряда определить тарифные ставки, соответствующие другим разрядам. 

Пример 4. Общий заработок бригады составляет 21988 руб. В составе бригады работали слесарь 6-го разряда – 178 ч (часовая ставка 42 руб.), слесарь – 4-го разряда – 100 ч (часовая ставка 31,2 руб.), слесарь 2-го разряда – 78 ч (часовая ставка 24 руб.). Определить заработок каждого члена бригады, если тарифные коэффициенты у слесаря  6-го разряда – 1,985, 4-го разряда – 1,474, 2-го – 1,134.

Определим тарифный заработок каждого рабочего.

Слесарь 6-го разряда 42 ∙ 178 = 7476 (руб.),

4-го разряда 31,2 ∙ 100 = 3120 (руб.), 2-го разряда 24 ∙ 78 = 1872 (руб.).

Всего – 12468 руб.

Отсюда, исходя из формулы (1), сдельный заработок каждого члена бригады составит:

Слесарь 6 разряда – ^_ ^21988_747613184,3(руб.),

12468

4 разряда – ^_ ^21988_31205502,3(руб.), 12468

2 разряда – ^_ ^21988_18723301,3 (руб.).

12468

Далее учащимся сообщается, что для повышения материальной и моральной заинтересованности рабочих в повышении производительности труда применяют различные премиальные системы оплаты труда. К ним относятся повременно-премиальная, сдельно-премиальная, аккордная и др. Премии выплачиваются за выполнение и перевыполнение плана, за выпуск бездефектной продукции, за экономию сырья и материалов и т. п. Премии устанавливаются руководителями промышленных предприятий, она составляет определенный процент от основного заработка.

Общий заработок рабочего, представляющий математическую модель заработной платы, выглядит так:

З₀  З (1 ( ^ )), 100

где З₀ – общий заработок; – процент премирования; З – заработок. Зачастую при решения этих задач используется сборник «Единые нормы и расценки» (ЕНиР).  

Пример 5. Рабочий в течение месяца выполнил следующие работы:

1.                Доработку грунта III группы в котлованах под фундаменты – 15 м³ (1м³ – 120 руб.).

2.                Укладку фундаментных блоков башенным краном весом до 3,5 т. – 10 шт. (1 шт. – 150 руб.).

3.                Установку блоков под стены подвалов весом до 2,5 т – 20 шт. (1 шт. – 100 руб.).

4.                Укладку панелей перекрытия площадью до 10 м² – 15 шт. (1 м² – 20 руб.).

Определить месячный заработок рабочего.

Решение. Месячный заработок рабочего будет состоять из суммы заработков по отдельным видам работ. Определим каждый из них в отдельности (цены договорные).

1.   Доработка грунта 120151800 (руб).

2.   Укладка фундаментных блоков 150101500 (руб.).

3.   Установка блоков под стены подвалов 10 ∙ 20 = 2000 (руб.).

4.   Укладка панелей перекрытия 200153000 (руб.). 

Итого заработная плата рабочего в течение месяца составит 8300 руб.

После решения этих задач обращается внимание учащихся на то обстоятельство, что для изготовления единицы продукции или какой-нибудь другой работы необходимо проделать ряд промежуточных работ. Например, для изготовления оконных блоков потребуется произвести распилку леса, затем острожку, зашпиливание швов, долбление, зачистку, разметку и сборку деталей, наконец, укладку готовой продукции в штабель. В стоимость изготовленной продукции будут входить все стоимости перечисленных работ с учетом времени, которые описываются калькуляцией. Отмечается, что с помощью составленной калькуляции определяют себестоимость изготовленной продукции и время, затраченное на ее изготовление. Калькуляции помогают при начислении заработной платы рабочим, облегчают описание выполненной работы. С учащимися можно рассмотреть наиболее простейшие виды калькуляций. 

Пример 6. Плотники, улучшив технологию производства, заменив  отдельные этапы производства продукции ручной труд механизированным, в течение трех лет дважды равномерно снизили себестоимость изготовления оконной коробки на один и тот же процент по сравнению с первоначальной стоимостью. На сколько процентов снизилась себестоимость оконной коробки, если согласно калькуляции она составляет 21,3 руб., а после снижения 18,7 руб.

Решение. Пусть х – процент снижения себестоимости изготовления оконной коробки. Тогда согласно условию задачи, составим уравнение:

                                          2x                42,6 x  260, откуда x 6%.

21,321,3 18,7 , 100

Следовательно, себестоимость снизилась на 6%. При решении задач такого вида учащиеся убеждаются, что производительность труда прямо связана с себестоимостью продукции: с ростом производительности труда себестоимость снижается.

Охарактеризуем описанные выше этапы решения задачи на следующем примере.  

Пример 7. Две бригады, состоящие из 10 и 20 человек, усовершенствовали технологию производства, а потому производительность труда, соответственно, возросла на 20% и 10%, и обе бригады за смену вместо 710 деталей стали изготовлять 816 деталей. Найти производительность труда каждого рабочего первой и второй бригады за смену до и после усовершенствования технологии производства. 

1. Этап формализации. 

доске одного из учеников, который выполняет решение задачи. 

Решение.

Пусть х деталей – производительность труда за смену одного рабочего первой бригады, а у деталей – производительность труда за смену одного рабочего второй бригады, тогда 10х+12у = 710. Производительность труда, соответственно, возросла на 20% и 10%, а потому получим второе уравнение: 0,2х+0,1у = 106. 

Итак, получили систему уравнений: .

Ученик быстро вычисляет искомые величины и пишет ответ, что производительность труда до улучшения технологии производства рабочего первой бригады за смену 35 деталей, а рабочего второй бригады – 30 деталей. После повышения производительности труда соответственно: 42 и 33. 

3. Этап интерпретации. На этом этапе осуществляется анализ решения задачи, еще раз повторяется использованная теория, подводятся итоги работы. 

                                                                                    деленный промежуток времени.

                    Можно ли говорить о производи-                   Да. 

тельности труда за одну неделю.                                     

Что понимают под технологией про- Под технологией производства имеют в изводства? виду способы обработки, применяемые при     изготовлении той или иной продукции.

Давай те проверим, правильно ли Проверка решения. Задача решена решена задача?

верно.

Таким образом, можно сделать вывод, что решение задач с экономическим содержанием способствует формированию экономических понятий и развитию мышления на этапах формализации и интерпретации задач с практическим содержанием.

При решении  задач, содержащих сведения об оплате труда, учащиеся начинают понимать, что с ростом производительности труда растет и заработная плата, что производительность труда связана с себестоимостью выпускаемой продукции, т. е. устанавливают взаимосвязи экономических явлений. 

2.3. Методические особенности обучения учащихся решению экономических задач с помощью линейных, квадратичных функций и неравенств

В экономических задачах часто встречаются зависимости, которые выражаются линейной функцией. В экономике линейная функция может выражать зависимость между ценой товара и спросом, между нормой прибыли и прибавочной стоимостью, между производством продукции и расходом материала и т. д. 

Рассмотрим методику обучения учащихся решению математических задач с экономическим содержанием, сводящихся к составлению линейных, квадратичных функций и неравенств с последующим их решением. Эти задачи требуют предварительного повторения с учащимися определенных тем: линейная функция, квадратичная функция, квадратные уравнения, системы линейных уравнений, неравенства, системы и совокупности неравенств.

Основная сложность, возникающая у учащихся при решении такого рода задач – построение математической модели – выбор неизвестной и запись условия задачи в формализованном виде. От того, насколько удачно выбрана неизвестная величина, зависит трудоемкость, а в некоторых случаях и возможность решения задачи.

Приведем несколько советов для учащихся, полезных при решении текстовых задач на составление уравнений и неравенств:

1.    Внимательно, может быть не один раз, прочитайте условие задачи с тем, чтобы стало понятно ее содержание.

2.    Часто бывает полезно сделать рисунок с отмеченными на нем числовыми данными.

3.    При очередном прочтении задачи нужно постепенно вводить неизвестные, при необходимости отмечая их размерности. Выбор неизвестных должен быть, в первую очередь, удобен для математической записи условий задачи, а не ориентирован на ее вопрос.

4.    При очередном прочтении задачи нужно записывать связи между известными и неизвестными величинами в виде уравнений и неравенств.

5.    Перед решением системы уравнений или неравенств нужно определить искомую величину, имея ввиду, что часто из полученной системы требуется найти только одну неизвестную или некоторую комбинацию неизвестных, что может быть сделано далеко не всегда.

6.    Если система допускает несколько решений, то проверить каждое из них. Чтобы учащиеся привыкли к задачам, требующих составления неравенств.

Прежде чем приступать к решению сложных текстовых задач с экономическим содержанием рассмотрим с учащимися простейшие примеры,  для проверки теоретического материала, устного счета и т. д. 

Например: Одно из натуральных чисел на 4 меньше другого. Причем квадрат меньшего из чисел не больше, чем удвоенное второе число. Найдите меньшее число из данных чисел.

                Учитель                                                           Ученик

Что надо сделать, чтобы отве- Построить ее математическую модель. тить на вопрос задачи?   𝑥² ≤2(𝑥+4)

Что представляет математиче- Неравенство. ская модель этой задачи?  

Что такое неравенство?       Соотношение между величинами, пока    зывающее, что одна величина больше или

                 Какие виды неравенств вы знае-     меньше другой.

те?       Линейные неравенства, квадратные не     равенства, рациональные неравенства, неравен-

                  Что называется решением нера-      ства, содержащие знак модуля.

венства?  Значение переменной х, которое обра щает неравенство f(x) >0 в верное числовое не-

                Что значит решить неравенство?      равенство, называют решением неравенства.

Какие правила используют при Решить неравенство, значит найти все решении неравенств?  его решения или доказать, что их нет.

К какому виду относится данное Правила равносильных преобразований. неравенство?  Квадратное.

Какие методы решения квадрат- ных неравенств вы знаете?

Рассмотрим пример простейшей линейной зависимости - прямую пропорциональность.

Известно, что на выплавку 1 т чугуна потребляется 1,5 т каменного угля. Следовательно, эта зависимость выразится формулой y =1,5x, где у – количество выплавленного чугуна; x – количество израсходованного угля; 1,5 – коэффициент пропорциональности. В общем случае, если на 1 т чугуна потребовалось бы не 1,5, а k т угля, то уравнение зависимости записывалось бы в виде y = kx.

Функция y = kx+b состоит из двух слагаемых и может выразить себестоимость выпускаемой продукции. В общую себестоимость входят расходы, которые зависят от выпуска продукции и расходы, которые от них не зависят. Назовем их условно расходами первой и второй группы. К расходам первой группы относятся: сумма денег, израсходованная на сырье, сумма денег, выплаченная рабочим. К расходам второй группы относятся: заработная плата служащих, отопление здания, освещение и т. д., т. е. расходы, которые не зависят от размера выпуска продукции. Если расходы первой группы обозначить через k, a второй группы – через b, то себестоимость С при выпуске продукции x составит: С = kx + b.

В данном уравнении при x<0 задача теряет смысл, при x = 0 – производство остановлено, при x>0 постоянно увеличиваются расходы первой группы, влекущие одновременное увеличение расходов второй группы за счет расширения предприятия, построения новых  объектов.

В экономических расчетах используются также уравнения прямой в виде:

y – y₁ = k (x – x₁) – уравнение прямой, проходящей через данную точку

с данным угловым коэффициентом. yy₁   xx₁

 – уравнение прямой, проходящей через две данные y2 y1 x2 x1 точки.

(x₁ ; y₁) – координаты первой точки;

(x₂ ; y₂) – координаты второй точки, х₁ ≠ х₂ , у₁ ≠ у₂. x y

     1 – уравнение прямой в отрезках. a b

Уравнение прямой в отрезках может выражать стоимость основных средств с учетом износа. Если считать, что любая машина переносит свою стоимость на изготовляемую продукцию с ее помощью равномерно, то ее стоимость будет уменьшаться линейно. В этом случае на оси у откладываем отрезок, отвечающий первоначальной стоимости, а на оси x – срок ее службы. Построим график функции для b = 52 тыс. рублей и a = 8 лет

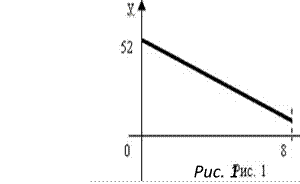
        На рассмотренных ниже примерах проиллюстрируем составление математических моделей и методику решения получаемых линейных, квадратичных функций и неравенств.

Пример 1. Себестоимость перевозки груза двумя видами транспорта выражается функциями С = 0,25х–1,6 (шоссейная дорога) и С = 0,2х+3,6 (железная дорога), где 10 ≤ х ≤ 1000  – расстояние в км, а С – транспортные расходы. Определить, какой вид транспорта выгоднее для перевозки одного и того же груза, и начиная с какого расстояния?

Решение

При x = 100 для первого вида транспорта стоимость перевозки составляет 23,4 руб., а для второго – 23,8 руб. При x = 300 стоимость первого вида транспорта составляет 73,4 руб., а второго – 63,8 руб. Следовательно, на малых расстояниях выгоднее перевозить груз по шоссейной дороге, а на больших – по железной дороге.

Выясняем с учащимися, начиная с какого расстояния выгодно пользоваться вторым видом транспорта?

Очевидно, что на определенном расстоянии стоимость перевозки тем или другим видом транспорта обходится одинаково. Это расстояние мы найдем, решив совместно данные уравнения:  С 0,25x1,6

                                                                                           , откуда 0,25х – 1,6 = 0,2х + 3,8 или х =

                                ^{C 0,2x 3,8,}

108.

Значит, начиная с 108 км, второй вид транспорта экономичнее (рентабельнее).

Учащимся объясняем, что эта задача сводится к нахождению абсциссы точки пересечения двух прямых.

Пример 2. Себестоимость производства стальных угольников бригадой из 5 чел. на Ставропольском инструментальном заводе в количестве 1400 шт. составляет 680 руб., а при выпуске 4500 шт. – 1900 руб. Определить себестоимость продукции: а) 2700 угольников; б) 5480 угольников.

Решение

Сравним выпуск продукции во втором и первом случаях. Себестоимость производства продукции больше на (1900 – 680) руб., а количество продукции на (4500 –1400) ед.

Если выпускается заводом x ед. продукции, то при сравнении с выпуском в первом случае себестоимость составит (C – 680) руб., а количество (х – 1400) ед. В этом случае разница себестоимости будет пропорциональна разнице выпуска, то есть 

                    С  680          x 1400

                                                               , откуда С = 0,394х + 128,4.

                 1900 680     45001400

Эта функция является экономико-математической моделью себестоимости выпуска продукции. По этой функции определяется себестоимость выпускаемой продукции данным заводом.

Себестоимость производства при выпуске 2700 угольников составит:

С(2700)  0,39427001291192,2 (руб.).

Себестоимость выпуска 5400 угольников составит: 

С(5400)  0,3945400129 2256,0 (руб.).

Себестоимость единицы продукции С₁ будет равняться:

                              С 0,394x 129                   129

С₁                0,394        . x x          x

Себестоимость для случая 

       а) С₁  = 0,44 (руб.).

       б) С₁ = 0,42 (руб.).

Следовательно, для случая б) производство стальных угольников будет выгоднее, а увеличение выпуска продукции ведет к снижению ее себестоимости.

Пример 3. Две бригады фрезеровщиков из 8 и 10 человек за смену изготовляли 700 деталей. После повышения производительности труда они стали изготовлять 770 деталей. Найти: 

а) на сколько процентов увеличилась производительность труда, если

каждый рабочий второй бригады до усовершенствования технологии производства за смену изготовлял на 7 деталей больше, чем рабочий первой бригады; 

б) среднемесячный заработок рабочего до и после усовершенствования технологии производства, если за каждую деталь оплачивают по 10 руб., а каждая деталь, изготовленная сверх нормы, по договору оплачивается на 50% больше. Число рабочих дней в месяце принять 22.

Решение:

Пусть x деталей – сменная производительность труда рабочих первой бригады, тогда (x + 7) деталей – сменная производительность труда рабочих второй бригады. Из условия задачи следует, что 8x 10(x  7)  700.

Предположим, что производительность труда увеличилась на y% .

8x

Тогда,   y – число деталей, дополнительно изготовленных рабочими 100

первой бригады за смену после повышения производительности труда, а   y – число деталей, дополнительно изготовленных рабочими второй

бригады за смену. Исходя из условия задачи, получим:

                  8x        10(x  7)

                          y                   y  70 .

                 100            100

Составим систему: 8x 10(x  7)  700,



 8x y  10(x  7)  y  70.

                100              100



Из первого уравнения получим x = 35. 

Тогда количество деталей, изготавливаемых рабочим второй бригады, составляет 42.

а) Величину повышения производительности труда найдем из второго

уравнения: у = 10%.

б) Найдем среднемесячный заработок рабочих первой и второй бригад.

До усовершенствования технологии производства:

3522 = 770 (деталей) – месячная производительность труда рабочего первой бригады;

4222 = 924 (деталей) – месячная производительность труда рабочего второй бригады;

107707700 (руб.) – среднемесячный заработок рабочего первой бригады;

10924=9240 (руб.) – среднемесячный заработок рабочего второй бригады.

Производительность труда после усовершенствования технологии производства:

                   770                                                 924

                10%  77 (деталей)  и   10%  92 (детали).

                 100%                                              100%

Таким образом, месячная производительность труда рабочих первой и второй бригад увеличилась соответственно на 77 и 92 детали.

По условию задачи деталь, произведенная сверх нормы, оплачивается на 50% больше; следовательно, за каждую деталь рабочему платят по 15 руб. Вычислим месячный заработок рабочих первой и второй бригад.

Заработок рабочего первой бригады составит 8855 руб., а второй – 10620 руб.

Итак, при решении экономических задач с помощью линейных, квадратичных функций и неравенств важно уметь составлять математические модели. При этом большое значение имеет правильно выбранная  неизвестная величина и запись условия задачи в формализованном виде. От того, насколько удачно выбрана неизвестная величина зависит возможность решения задачи.

2.4    Анализ педагогического опыта обучения учащихся решению текстовых задач с экономическим содержанием

При проведении исследования нами были изучены источники литературы, в которых рассматриваются вопросы методики обучения учащихся решению текстовых задач с экономическим содержанием. В ходе работы мы провели классификацию литературы, условно разделив ее на две группы. В первую группу мы включили источники, характеризующие методические основы обучения учащихся решению текстовых задач с экономическим содержанием, а во вторую – те, в которых описано подробное решение текстовых задач с экономическим содержанием. В этом  параграфе мы проведем анализ каждой из них.

    Начнем с первой группы.

Р. Коврикова [10] предлагает внедрение в курс математики в школе экономико-математических задач, для того чтобы учащиеся получили представление об экономике и экономических процессах, и могли легко ориентироваться в потоке экономической информации.

Ш.А. Музенитов [15] раскрывает проблемы экономического образования и воспитания учащихся средствами математики через спецкурс «Математическая  экономика», направленный  развитие экономического мышления. Приводит широкий набор задач по главам с подробными решениями всех задач. 

В.А. Далингер [8] предлагает рассматривать прикладные задачи экономического содержания двух видов:

1)                математические задачи с экономическим наполнением, направленные на формирование основных математических понятий, а также умений и навыков решения типичных математических задач. Такие задачи подчинены структуре: экономика - математика;

2)                экономические задачи, при решении которых используются математические методы.

Далее охарактеризуем вторую группу источников. Здесь мы отметим те из них, в которых описано подробное решение текстовых задач с экономическим содержанием.

Ф.Ф. Лысенко [12] рассматривает приемы, полезные при решении заданий с экономическим содержанием на конкретных примерах. Приводит теоретическую информацию и ряд задач для самостоятельного решения. Этим пособием могут руководствоваться учителя при подготовке учащихся к ЕГЭ по математике.

Н.П. Пучков [19] уделяет особое внимание вопросам математического моделирования простейших экономических явлений, не требующих специальных экономических знаний, на использование процентов, алгебраических уравнений. Дает указания по решению уравнений в целых числах и применение линейных методов решения текстовых задач с экономическим содержанием.

Д.Д. Гущин [7]предлагает план проведения курса финансовой математики для учащихся, проявляющих интерес к анализу и применению математических алгоритмов в экономике. Особенностью курса является его нацеленность на анализ реальных экономических проблем и практическую значимость результатов, полученных в ходе учебной деятельности.

Итак, проведенный обзор педагогических исследований позволил нам, сделать вывод о том, что в настоящее время существует небольшое количество источников информации рассматриваемых методику обучения учащихся решению текстовых задач экономического содержания. Существующие источники не позволяют в полной мере осветить данную тему. Это обусловлено тем, что до недавнего времени не было потребности в литературе, в которой рассматриваются вопросы методики обучения учащихся решению текстовых задач с экономическим содержанием. Необходимость создания такой литературы появилась недавно. Это связано с тем, что в 2015 году ЕГЭ по математике претерпел изменения: с целью оптимизации структуры варианта в условиях перехода к двухуровневому экзамену во вторую часть было добавлено задание профильного уровня (19) с экономическим содержанием.

Далее уделим вниманию использованию математических задач экономического содержания, требующих умения обращаться с процентами. Это обусловлено тем, что проценты широко распространены в реальной жизни при проведении различных операций, где возникают банковские проценты, проценты от зарплаты в качестве налога и т.д.

Мы провели анализ материалов сайта Фестиваль педагогических идей «Открытый урок» http://festival.1september.ru, в которых рассматриваются вопросы, методики обучения учащихся решению текстовых задач с экономическим содержанием на использование процентов.

М.В. Величко и А.А. Моргунова [6] акцентируют внимание на то, что основной задачей системы образования становится формирование личности – разносторонне образованной, обладающей высоким уровнем экономической культуры, и способной делать оптимальный экономический выбор. Исходя из этого, они считают, что обучение учащихся решению задач на проценты есть средство их подготовки к жизненному самоопределению. Их основная идея состоит в том, чтобы углубить изучение темы «Проценты» в 5 и 6 классах. Они рекомендуют  знакомить обучаемых с формой неявного использования процентов, типичной для средств массовой информации. Задачи со сложными процентами необходимо рассматривать на кружковых занятиях. 

З.З. Садикзянова [20] предлагает конспект урока, цель которого - ознакомление с формулами «сложных процентов» и формирование навыков применения этих формул при решении задач. Для успешной выработки практических навыков по теме она предлагает работу в группах. Для учащихся каждой группы ею разработаны индивидуальные карточки. 

Ю.В. Васенкова [5] знакомит с основами экономики и предпринимательства через решение текстовых математических задач на проценты. В условиях задач встречаются такие понятия и термины как фирма, покупатель, клиент, конкурент, производство, монополия, цена и др. Каждому из них дано определение. 

Г.А. Мирьякупова [14]  предлагает изучение темы «Сложные проценты» в системе нетрадиционно построенных учебных занятий, где особое значение имеют: урок – лекция, уроки решения ключевых задач, уроки – консультации, зачетные уроки. Эти тему полезно параллельно рассматривать используя классические приемы, а на этапе закрепления темы можно решать задачи по группам. Тогда у учащихся формируется целостное представление о способах решения задач данного типа. 

Л.И. Петухова [18] утверждает, что при решении текстовых задач различными методами у учащихся вырабатываются определённые умения и навыки, которые в процессе дальнейшего обучения должны совершенствоваться и закрепляться. Примерами таких умений и навыков служат:

1)                Нахождение процентного отношения двух величин (чисел).

2)                Понятие производительности труда.

3)                Нахождение стоимости товара, акции.

4)                Нахождение прибыли.

5)                Нахождение себестоимости продукции.

6)                Расчёт начислений банка на вклады.

Н.Н. Тимошенко [25] предлагает разработку элективного курса с целью  формирования умения решать задачи с экономическим содержанием основных типов. Данная разработка представляет ценность тем, что курс рассчитан не только для будущих экономистов, но и для всех людей, так как те задачи, которые представлены в данном курсе демонстрируют практическую ценность математики, позволяют активизировать учебную деятельность, формируют знания и способности к деятельности которые актуальны и востребованы практикой, рынком труда.

Итак, проведенный анализ материалов сайта Фестиваль педагогических идей «Открытый урок» позволил нам, сделать вывод о том, что материалы посвященные теме использования математических задач экономического содержания, требующих умения обращаться с процентами в полной мере раскрывают данную тему. Представленный материал позволяет показать широту применения такого простого и известного учащимся математического аппарата, как процентные вычисления. Ценность представленных материалов в том, что они демонстрируют широкий спектр применения расчета процентов в торговле и экономических сферах, т.е. тесную взаимосвязь математики с торговлей и экономикой.

Заключение

Подведем итоги проведенного нами исследования. Цель исследования  заключалась в том, чтобы описать методику обучения учащихся решению текстовых задач с экономическим содержанием. Для достижения данной цели перед началом работы был поставлен ряд задач.

При решении первой задачи были рассмотрены работы таких ученых как И.В. Арнольд, В.А. Далингер, Ю.М. Колягин, Л.М. Фридман и др. Эти работы создали прочный фундамент для становления и дальнейшего развития теории задач в обучении математике.  

 При решении второй задачи:

1)    описана история использования текстовых задач в процессе обучения. Что позволило делать вывод о том, что применение текстовых задач  зародилось еще в древности, а методика обучения решения задач была разработана достаточно хорошо лишь в середине XX века;

2)    охарактеризованы различные подходы к определению понятий «задача» и «текстовая задача». В различных определениях эти понятия рассматриваются под различными углами зрения и соответственно наполняются различным содержанием.  Каждое определение построено для достижения определенных целей. В конкретных ситуациях договариваются в рамках какого определения происходит рассмотрение данных понятий;

3)    рассмотрена классификация текстовых задач по различным основаниям. Отметим, что всякая типология задач является условной, а отнесение ее к тому или иному виду зависит от того, кто решает задачу. Несмотря на это, различные типологии позволяют учителю более осознанно подходить к отбору задач в зависимости от целей обучения;

4)    выделены основные методы решения текстовых задач. К ним относят: арифметический, алгебраический, графический, геометрический. Знание различных методов решения помогают развивать у учащихся логическое мышление, формирования межпредметных связей. Следует отметить, что практически каждая задача в рамках выбранного метода допускает решение различными способами, т.е. решение с помощью различных моделей.

При решении третьей задачи была описана методика обучения учащихся решению текстовых задач с экономическим содержанием. При этом отдельное внимание уделялось обучению школьников переводу текста задачи на математический язык, то есть умению составлять математические модели реальных ситуаций, формированию умения выявлять связи и зависимости между величинами.

При решении четвертой задачи был проведен анализ педагогического опыта методики обучения учащихся решению текстовых задач с экономическим содержанием. Мы убедились, что в настоящее время существует небольшое количество источников литературы, в которых рассматривается методика обучения учащихся решению текстовых задач с экономическим содержанием. Существующие источники не позволяют в полной мере осветить данную тему. Это обусловлено тем, что до недавнего времени не было потребности в литературе, в которой рассматриваются вопросы методики обучения учащихся решению текстовых задач с экономическим содержанием. Необходимость создания такой литературы появилась недавно. В частности, это связано с тем, что в 2015 году ЕГЭ по математике претерпел изменения: с целью оптимизации структуры варианта в условиях перехода к двухуровневому экзамену во вторую часть было добавлено задание профильного уровня с экономическим содержанием.

Таким образом, все задачи, сформулированные во введении, решены и можно говорить о достижении цели исследования.

Список литературы

1.     Арнольд И.В. Принципы отбора и составления арифметических задач/Вопросы методики математики. – М., – 1946.  – С. 7–28. – (Изд. АПН РСФСР, вып. 6).

2.     Баженова Н.Г. Теория и методика решения текстовых задач. - М.: Флинта, 2012.

3.     Байрамукова П.У. Методика обучения математике в начальных классах. – Ростов н/Д: Феникс, 2009.

4.     Балл Г.А. Теория учебных задач: Психолого-педагогический аспект. - М.: Педагогика, 1990. 

5.     Васенкова Ю.В. Экономико-математические задачи на проценты в предпринимательстве [Электронный ресурс] //URL: http://project.1september.ru/works/584167 [Дата доступа: 04.05.2016].

6.     Величко М.В., Моргунова А.А. Методика организации по обучению решения задач на проценты как средство подготовки учащихся к жизненному самоопределению [Электронный ресурс] //URL: http://festival.1september.ru/articles/652399/ [Дата доступа: 04.05.2016].

7.     Гущин Д.Д. Встречи с финансовой математикой. – Санкт - Петербург, 2016.

8.     Далингер В.А. Прикладные математические задачи с экономическим содержанием как средство профориентации учащихся// Международный журнал экспериментального образования. – 2013.- №11. – с.143145.

9.     Демидова Т.Е., Тонких А.П. Теория и практика решения текстовых задач. - М.: Издательский центр «Академия», 2002. 

10.                        Коврикова Р.      Методология       внедрения экономико-

математических задач в доуниверситетский курс математики. //Revista Stiintifica a Universitatii de Stat din Moldova. – 2013.- № 9. – с.162-170.

11.                        Колягин Ю.М. Функции задач в обучении математике и развитие мышления школьников / Советская педагогика,  № 6, 1974. – c. 56-61.

12.                        Лысенко Ф.Ф., Калабухова С.Ю. Математика. Подготовка к ЕГЭ. – Ростов-на-Дону: Легион, 2015.

13.                        Магницкий Л.Ф. Арифметика [Электронный ресурс] //URL: http://math.ru/lib/176 [Дата доступа: 10.10.2015].

14.                        Мирьякупова Г.А. Решение задач при изучении темы «Сложные проценты» [Электронный ресурс] //URL: http://festival.1september.ru/articles/633864/ [Дата доступа: 04.05.2016].

15.                        Музенитов  Ш.А. Математическая экономика / Ш.А. Музенитов, Б.М. Синельников, Э.Ш. Музенитов. – Ставрополь : СевКав ГТУ, 2003.

16.                        Овчинникова М.В. Методика работы над текстовыми задачами в начальных классах– К.: Пед.пресса, 2001.

17.                        Паньков А.В. Применение компьютерных математических систем для решения задач с экономическим содержанием на уроках математики в школе [Электронный ресурс] //URL:

http://lib.herzen.spb.ru/media/magazines/contents/1/37(80)/pankov_izv37_80_p

467_472.pdf [Дата доступа: 04.05.2016].

18.                        Петухова Л.И. О решении текстовых задач по математике

[Электронный ресурс] //URL: http://festival.1september.ru/articles/103564/

[Дата доступа: 04.05.2016].

19.                        Пучков Н.П., Денисова А.Л., Щербакова А.В. Математика в экономике. - Тамбов: Издательство ТГПУ, 2002.

20.                        Садикзянова З.З. Решение задач на проценты с экономиче-

ским содержанием [Электронный ресурс] //URL: http://festival.1september.ru/articles/515170/ [Дата доступа: 04.05.2016].

21.                        Симонов А.C. Математические модели экономики. - Тула,

2000. 

22.                        Симонов А.С. Экономика на уроках математики. – М.:

Школа-Пресс, 1999. 

23.                        Стефанова Н.Л.  Методика и технология обучения математике. – М.: Дрофа, 2007. 

24.                        Стойлова Л.П. Математика. – М.: Академия, 2002.

25.                        Тимошенко Н.Н. Элективный курс «Задачи с экономиче-

ским содержанием» [Электронный ресурс] //URL: http://festival.1september.ru/articles/654339/ [Дата доступа: 04.05.2016].

26.                        Фридман Л.М. Сюжетные задачи по математике. История, теория, методика. – М: Школьная пресса, 2002.

27.                        Фридман Л.М., Турецкий Е.Н. Как научится решать задачи. – М.: Просвещение, 1989.

28.                        Шевкин А.В. Из истории использования текстовых задач в

        России.                                [Электронный                ресурс]                 //URL:  

http://www.shevkin.ru/?action=Page&ID=399 [Дата доступа: 12.10.2015]

29.                        Шелехова Л.В. Сюжетные задачи по математике. – М.-

Берлин: Директ-Медиа, 2015.

Приложение 1.

Схема 1. Классификация текстовых задач 

(автор Л.М. Фридман и Е.Н. Турецкий, Стефанова Н.Л.)

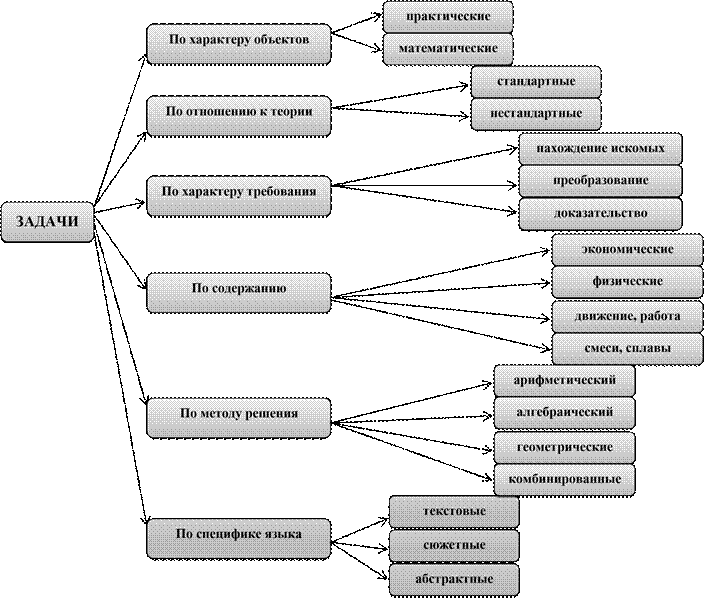
Приложение 2. Пример решения задачи различными методами Пример. Чтобы доставить письмо за 2 ч 40 мин из А в В, расстояние между которыми 70,5 км, почтальон ехал сначала на велосипеде со скоростью 12,75 км/ч, а затем на мотоцикле со скоростью 67,5 км/ч. Сколько времени ехал почтальон на велосипеде и сколько на мотоцикле?  I (арифметический метод) 

1)                      = 34 (км) - проехал бы почтальон, если бы все 2 ч 40 мин.

Ехал на велосипеде; 

2)                70,5 - 34 = 36,5 (км) - расстояние, которое осталось бы проехать на мотоцикле;

3)                67,5 - 12,75 = 54,75 (км/ч) - разность скоростей мотоцикла и велосипеда; 

4)                36,5 : 54,75 = ²        - он ехал на мотоцикле; 

5)                         = 2 (ч) - ехал на велосипеде. 

II       (алгебраический метод) 

Пусть х часов почтальон ехал на велосипеде, тогда ( - время движения на мотоцикле. Путь, пройденный на велосипеде 12,75 ∙ х км, а путь, пройденный на мотоцикле 67,5х). Так как весь путь 70,5 км, составим уравнение: 

                12,75х + 67,5 х) = 70,5 

Решая данное уравнение, получаем х = 2 (ч). 

III   (графический метод)

На оси абсцисс откладывается время, на оси ординат - расстояние. В таком случае абсцисса любой точки графика движения указывает момент времени, а ордината той же точки - в каком месте пути в этот момент находится точка. Если на одном чертеже построены два графика движения, причем графики движения пересекаются в некоторой точке, то абсцисса точки пересечения показывает время встречи движущихся объектов, а ордината место встречи. 

Движение на велосипеде задается графиком функции s = 12,75t, на мотоцикле s = 67,5t + b . Учитывая, что график проходит через точку (; 70,5

), находим b = -109,5. Точка пересечения графиков находится решением системы уравнений: t = 2, s = 25,5.

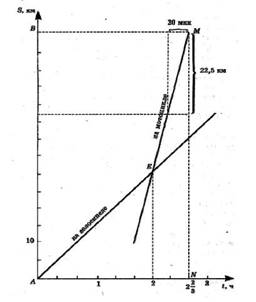
IV   (геометрический метод) 

Ot - ось времени, Оv - ось скорости; 12,75 - скорость велосипедиста, 67,5 - скорость мотоциклиста; t- время, затраченное почтальоном на движение на велосипеде. 

Путь, пройденный почтальоном, можно представить в виде суммы площадей прямоугольников 𝑆₁ и 𝑆₂ или площадью прямоугольника со стороной 67,5 и без площади прямоугольника 𝑆₃ , то есть 𝑆₁ + 𝑆₂ = 𝑆 = 70,5 (км) или = (67,5 -12,75)t, имеем 67,5 t

=70,5.t =2.

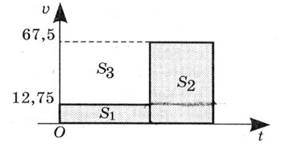
Таким образом, мы увидели, что существуют различные методы решения текстовых задач, которые  позволяю решать задачи различными способами. Для развития обучающихся целесообразно показывать, что та или иная задача может быть решена несколькими различными методами, так как это позволит учащимся лучше усваивать материал, развивать функциональное мышление детей, а также умение отыскивать наиболее рациональные решения.

Приложение 3.

Словарь основных экономических понятий 1. Производительность труда – способность рабочего изготовить в течение рабочего времени определенное количество продукции.

2.                Себестоимость продукции – общая сумма затрат предприятия на производство единицы товара, выраженная в деньгах.

3.                Рентабельность – доходность, прибыльность общественных, частных предприятий, или отраслей народного хозяйства.

4.                Кредит – ссуда. Деньги, данные в долг на определенное время.

5.                Производственные фонды – средства производства, которыми оно располагает при осуществлении процесса производства.

6.                Нормой времени - называется то количество рабочего времени, которое потребуется рабочему определенной профессии и квалификации на производство единицы продукции или выполнение единицы другой работы.

7.                Норма выработки – количество изделий или единиц работы, произведенных в единицу времени.

8.                Тарифная ставка- оплаты труда за единицу времени.

9.                Расценка-  денежная стоимость в рублях единицы продукции или единицы выполненной работы.

10.            Спрос и предложение – количество товара, реализованного и предложенного в единицу времени.

11.            Заработная плата – это количество денежных средств, выплаченных рабочим и служащим за выпуск готовой продукции или за выполнение какой-нибудь другой работы.

12.            Трудовые ресурсы – это лица, находящиеся на государственной службе, работающие в различных предприятиях, организациях, учреждениях и других государственных секторах.

13.            Технический прогресс – процесс развития и совершенствования техники и технологий производства для интенсификации всех отраслей данного хозяйства.

14.            Режим экономии – это бережливое отношение к собственности предприятия, рациональное использование сырья, материальных, трудовых и денежных средств, устранение непроизводительных затрат и потерь  на производстве.

15.            Продукция – продукт труда для удовлетворения потребности общества и его членов.

16.            Качество продукции-  долговечность, надежность, прочность, сортность, экономичность в производстве и в эксплуатации. Качество продукции характеризует эффективность общественного или частного производства.

17.            Прибыль – разница между выручкой предприятия за проданную продукцию и затратами на ее производство и реализацию.

18.            Капиталовложения – финансовые средства, затрачиваемые на строительство новых, реконструкцию, расширение и техническое перевооружение действующих   предприятий, на жилищно-коммунальное и культурно-бытовое строительство.

19.            Амортизация – возмещение в денежной форме стоимости основных средств , постепенно переносимой ими на вновь созданный в процессе производства продукт.

20.            Калькуляция – определение величины затрат в денежном выражении, приходящихся на единицу продукции или на объем выполненных работ.

21.Рационализаторское предложение – предложение по усовершенствованию применяемой техники, усовершенствованию выпускаемой продукции, технологии производства, способов контроля, наблюдения и исследования или предложения, позволяющие повысить производительность труда, более эффективно использовать энергию, оборудование, материалы.

22.            Трудовой договор – соглашение между трудящимися и предприятием, учреждением, организацией, частной фирмой, по которому трудящийся обязуется выполнять работу по определенной специальности, квалификации или должности, а предприятие обязуется выплачивать заработную плату и обеспечивать условия труда, предусмотренные договором и соглашением сторон.

23.            Трудовая дисциплина – соблюдение определенного порядка, правил, установленных на производстве. Без должной трудовой дисциплины становится невозможным общественное производство. Современное производство состоит из множества взаимосвязанных процессов, которые должны быть четко согласованы между собой. Если кто-то не вышел на работу или недобросовестно выполнил свои обязанности, неизбежно нарушается весь процесс.

24.            Цена – денежное выражение стоимости. Цена товара указывает, что в нем воплощено столько же общественно необходимого труда, сколько в данной сумме денег. Цены товаров могут повышаться или понижаться как под влиянием изменения стоимости товара, так и в результате изменения стоимости денежного материала.

25.            Хозяйственный расчет – метод планового введения хозяйства, направленный на достижение максимальной эффективности производства.

26.            Бизнес – экономическая деятельность, дающая прибыль, приносящая доход или личные выгоды при любом виде предпринимательской деятельности.

27.            Предприниматель – юридическое или физическое лицо, деятельность которого в рамках действующего законодательства направлена на создание, функционирование, и развитие предприятия, ставящая своей целью сбыть производимую продукцию (услуг) с целью получения прибыли.

28.            Приватизация – передача (продажа) принадлежащих государству предприятий в частные руки.

29.            Процент – плата, получаемая кредитором от заемщика за использование предоставленными в ссуду денежными средствами.

30.            Рынок – совокупность экономических отношений в специально отведенном месте между продавцами и покупателями для решения собственных хозяйственных нужд и производственных потребностей.

31.            Инфляция – чрезмерное увеличение находящейся в обращении массы бумажных денег по сравнению с реальным предложением товаров, обеспечения бумажных денег, находящихся в обращении, т. е. падение их покупательной способности.

32.            Коммерсант – лицо, занимающееся частной торговлей коммерцией с целью получения прибыли.

33.            Кредитор – организация, предприятие или частное лицо, дающий что-либо в долг, предоставляющий денежные средства в кредит.

34.            Лицензия – специальное разрешение, получаемое от государственных органов на производство, ввоз или вывоз определенного количества товаров для производственной деятельности.

35.            Маклер – посредник при заключении сделок на фондовых, товарных и валютных биржах.

36.            Маркетинг – комплексная система организации производства и сбыта продукции, построенная на основе предварительного исследования нужд и потребностей покупателей с учетом экономической ситуации на данный момент.

37.            Менеджер – профессиональный управляющий, специалист по управлению производством.

38.            Налоги – обязательные платежи, взимаемые государством с физических и юридических лиц, являются основным источником бюджетных средств государства и местных органов управления.

39.            Реклама – информация о товарах, различных видах услуг с  целью создания спроса на эти товары и увеличения их популярности.

40.            Конкуренция – соперничество между товаропроизводителями  за более выгодные условия производства и сбыта товаров, за получение наибольшей прибыли.

41.            Инвестиция – долгосрочное вложение денег в какое-либо предприятие, коммерческое дело.

42.            Индекс – цифровой показатель, выражающий последовательные изменения какого-либо экономической ситуации, объема производства, цен, зарплаты, товарооборота.

43.            Валюта – денежная единица страны, денежный запас иностранных государств, а также кредитные средства обращения и платежа, используемые в международных расчетах.

44.            Облигация – вид ценной бумаги, по которой ее владельцу выплачивается ежегодный доход, размер которого заранее установлен в форме определенного процента к ее нарицательной стоимости. 

45.            Девальвация – уменьшение официального золотого содержания денежной единицы страны или снижение ее курса по отношению к валютам других стран.

46.            Депозит – денежные средства или ценные бумаги, помещаемые для хранения в кредитные учреждения.

47.            Акция – ценная бумага, удостоверяющая участие ее владельца в получении части прибыли акционерного общества.

48.            Дивиденд – доход, получаемый владельцем акции, который представляет собой часть прибыли акционерного общества.

49.            Конвертируемость – способность денежных; средств государства свободно обмениваться на любую иностранную валюту.

50.            Бюджет – 1) расклад денежных средств (расходов и доходов) государства, предприятия, учреждения на определенный период; 2) совокупность доходов и расходов лица, семьи за определенный период.