Модель Еванса

Модель Еванса           

У моделі Еванса розглядається ринок одного товару, час вважається безперервним. Нехай d(t), s(t), p(t) - відповідно попит,  пропозиція та ціна цього товару в момент t . Попит і пропозиція вважаються лінійними функціями ціни

d(p) = а - bp,(a, b) > 0,

 тобто попит з ростом ціни падає,

s(p) = +βp, < 0, β > 0,

тобто пропозиція з ростом ціни росте. Природно вважати, що  a > 0, тобто при нульовій ціні попит є (по-іншому говорячи, товар бажаний).

Основне припущення складається у тім, що ціна змінюється в залежності від співвідношень між попитом та пропозицією:

∆p = y(d-s) ∆t, y > 0,

тобто збільшення ціни прямо пропорційно перевищенню  попиту над пропозицією і тривалості цього перевищення.

  Отже, одержуємо диференціальне рівняння

dp/dt = y(d - s).

Підставляючи в це рівняння лінійні залежності попиту та пропозиції від ціни, одержуємо лінійне неоднорідне диференціальне рівняння з початковою умовою: 

                      dp/dt=-γ[(b+ β)p-(а-)], p(0)=p₀,                   (5.1)

Видно, що dp/dt > 0 при р* > р і dp/dt < 0 при р* < р. При цьому при 

р* > р  ціна прагне до р* зростаючи, а при р* > р — убуваючи. Сама ціна  р* єрівнозваженою ціною — при ній рівні попит та пропозиція:

р = (а-)/(b + β).

Рівнозважена ціна може бути знайдена також графічно як точка перетинання прямих попиту d(p) = a-bp  і пропозиції s(p) =  + βр (рис. 5.4).

      Звичайний метод рішення рівняння (5.1) - метод варіації постійної. Відповідно до цього методу загальне рішення є сума загального рішення відповідного однорідного рівняння dp/dt = -у(b + β)p і якого-небудь часткового рішення неоднорідного рівняння

р(t) = p_oe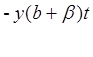 +[( а-а)/(b+β)][l-e- ],

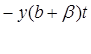або

р(t) = p_oe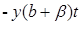 +p [1-e- ].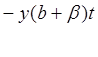

Розглянемо дискретний аналог  моделі  Еванса. У дискретній моделі ринок функціонує  в такий спосіб :   ранком   на ринку виявляються  деякі  пропозиція  і попит  .  У залежності від їхніх значень ціна починає рівномірно рости або убувати: якщо ранком попит був більше пропозиції, то зростати, якщо пропозиція була більше попиту, то убувати.

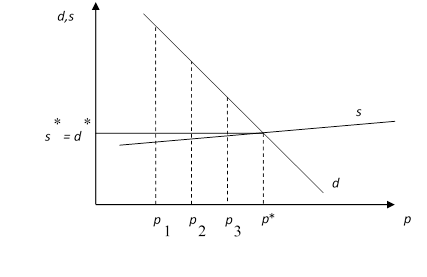
                                           Рис. 5.4                             

          Припустимо, що початкова ціна була , при цьому _.  Отже, ціна почне зростати За день вона зросте до деякого значення , при цьому знову буде і ціна буде зростати далі і далі, доки не досягне .