Моделирование в среде MathCAD, Maple

Моделирование в среде MathCAD, Maple

Для того, чтобы решить простейшее уравнение в среде MathCAD задаётся уравнение F(x)=0,затем выписываются отдельно коэффициенты этого уравнения.

тогда задаём x(1,-5.6) промежуток где лежит корень уравнения а затем вызывается функция А:=polyroots(x).

Для того, чтобы решить уравнение в среде Maple используют следующие функции:

Solve(f(x),x);

F(x) это уравнение, х – переменная,

или fsolse(f(x),x,p);

p-параметр, p=[-1,1], после каждой скобки знак ;

Замечание. Если необходимо решить уравнение в символьном виде, то для него используется функция solve(eq,var);

Eq- уравнение, var –переменная.

Для того чтобы, изобразить график в среде MathCAD, надо сначала указать диапазон изменения аргумента т.е. показать как меняется х и у.

x:=-5,-4.5..5

y:=-10,-9.5..10 нажав клавиши . . - :

Затем вызывается из меню график и задаётся на графике х и f(x).

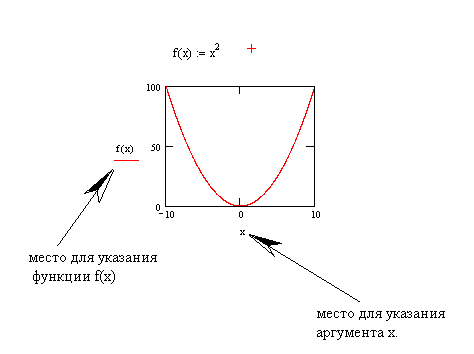
Для задания поверхности надо указать диапазоны, указать формулу, затем в меню «графики» вызываем «поверхность».

Все графики необходимо располагать строго после описания диапазонов и функций.

Maple позволяет решать уравнения и изображать графики функций.

Для построения графика указывается значение переменной (имя)

P:=plot(<функция 1>,<функция 2>,<диапазон для аргумента>): p;

Пример:

P;=plot(x³,x-1,x:=-2..2):p; - это пример решения уравнения x³-x-1.

Для моделирования  в среде Maple можно использовать построение графиков а также построение поверхностей.

Моделирование в среде MathCAD задачи «Хищники и жертвы».

В 1925 г. В Италии образовался союз двух учённых: математика Вито Вольтер и зоолог Д’Анконо. Рассматривалась задача о явлении, связанном с периодическим в несколько лет возрастанием и убыванием улова промысловых рыб. Статистика привела к следующему выводу: в период 1ой мировой войны интенсивность рыбной ловли в средиземном море резко снизилась, что привело к возрастанию числа хищных рыб, питающихся промысловыми  рыбами. В результате численность промысловых рыб резко упала, что в свою очередь привело к гибели части хищных рыб, потому что их пища стала исчезать.

Обсуждая данное явление они пришли к выводу, что помимо внешних факторов (смена времён года, климата) существует причины особого характера, влияющие на популяции животных.

Качественно описать словами данный процесс не представляется возможным, необходимо выразить явления с помощью формул и уравнений. Были проанализированы различные виды животных в разных местах планеты и сделаны следующие допущения модели:

1.пища (жертва) неограниченна средой обитания.

2.хищники питаются только жертвами.

3. прирост жертв пропорционален их численности.

4.убыль жертв пропорциональна произведению числа жертв и хищников.

5.прирост хищников пропорционален произведению числа хищников и жертв.

6.убыль хищников пропорциональны их числу.

Модель такого биоценоза с учётом введённых допущений определяется следующей системой из двух дифференциальных уравнений:

   (1)

N₁-жертвы (их число).

t-время

N₂-число хищников.

 (2)

 - коэффициент естественного прироста жертв.

 - коэффициент естественного прироста хищников.

-коэффициент уничтожения хищниками жертв.

-коэффициент защиты жертв от хищников.

Приведём уравнения 1 и 2 к нормированному виду:

где   относительное число жертв.

         относительное число хищников.

τ- нормированное время.

B=- коэффициент.

Составим по данной математической модели программу на языке MathCAD (см практику).

Статистические вычисления в среде MathCAD

Данные вычисления проводятся по следующим направлениям:

1.расчёт статистических параметров массива случайной последовательности чисел: среднее значение дисперсии, коэффициент корреляции и т.д.

2. расчёт различных  законов плотности с теории вероятности (нормальная, равномерная, биномиальная и т.д.)

3.пасчёт функции распределения вероятности Лапласа, Пуассона, Стьюдента и т.д.

4.генерирование случайной последовательности чисел с равномерными законами распределения вероятности.

Категория «случайные числа» находится в подменю «встроенные функции f(x)».

Краткое описание некоторых функций MathCAD.

rnorm(M,μ,σ) – генерирует случайную последовательность чисел, подчиняющихся нормальному  закону распределения.

Runf(M,a,b) - генерирует случайную последовательность чисел имеющих равномерное распределение внутри интервала (a,b)

Rnd(x) - генерирует случайную последовательность чисел имеющих равномерное распределение внутри интервала (0,x).

Категория «статистика» в подменю помогает вычислять среднее значения массива чисел путём обращения к функциям mean (M1,M2…) где M1,M2 – матрицы в которые собраны массивы обрабатываемых чисел.

Чтобы найти дисперсию массива чисел необходимо обратиться к функции var (M1,M2,…) 

Коэффициент корреляции двух массивов M1,M2 вычисляется с помощью функции corr(M1,M2).

При нормальном законе распределения вероятности функцию распределения вероятности считают как определённый интеграл от плотности вероятности. Этот интеграл вычисляется с помощью функции pnorm(x,μ,σ).