Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 3. Введение в анализ. Дифференциальные исчисления. Лекция № 5. Пределы и непрерывность.

Раздел 3. Введение в анализ. Дифференциальные исчисления.

Лекция № 5. Пределы и непрерывность. (2 часа)

План лекции:

1. Понятие предела числовой последовательности:

1.1  Определение числовой последовательности.

1.2  Предел числовой последовательности.

1.3  Свойства предела.

2. Понятие предела функции.

2.1  Определение предела функции.

2.2  Свойства предела функции.

2.3  Методы вычисления предела функции.

2.4  Бесконечно малые и бесконечно большие функции.

2.5  Непрерывность функции в точке и на интервале

Литература:

1.    Электронный ресурс. О_2: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 2: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 241 с. — (Профессиональное образование). — ISBN 978-5-534-10173-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442439, п. 6.1 – 6.10, стр.40.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₅.Структуру плана для решения задач;

З₆.Порядок оценки результатов решения задач профессиональной деятельности.

Основные понятия:

Числовой последовательностью называется бесконечное множество чисел (элементов), имеющих определенные номера. Эти числа являются членами последовательности:   x₁-первый член,  x₂-второй член,  ... , x_n-n-ый член. Числовая последовательность обозначается так: {x_n}.

Число А называется пределом числовой последовательности {x_n}, если для  такое, что для всех n>N выполняется условие .

Числовая последовательность, имеющая предел, называется сходящейся. Если же предел не существует или равен , то последовательность называется расходящейся.

Число а называется пределом функции  при , если для  такое, что для , для которых , выполняется неравенство . Пишут так: .

Число а называется левосторонним пределом функции f(x) при  (слева), если для   такое, что для , для которых , выполняется неравенство .

Число а называется правосторонним пределом функции f(x) при  (справа), если для   такое, что для , для которых , выполняется неравенство .

Если функция f(x) имеет предел в точке a , то она ограниченна в некоторой окрестности точки a.

Бесконечно малой величиной при  называется функция, предел которой в точке a равен 0.

Бесконечно большой величиной при  называется функция неограниченно возрастающая.

1. Предел числовой последовательности.

1.1. Определение числовой последовательности

Числовой последовательностью называется бесконечное множество чисел (элементов), имеющих определенные номера. Эти числа являются членами последовательности:   x₁-первый член,  x₂-второй член,  ... , x_n-n-ый член. Числовая последовательность обозначается так: {x_n}.

Числовую последовательность задают формулой n-го члена: x_n=f(n). Например, если  то    x₁=2,  , ...,  и т.д.

Числовую последовательность также можно задать рекуррентным соотношением: ,  x₁=1.

Тогда ,, и т.д.

1.2. Предел числовой последовательности

Определение. Число А называется пределом числовой последовательности {x_n}, если для  такое, что для всех n>N выполняется условие .

Это означает, что в любой окрестности точки А содержится бесконечное множество элементов последовательности.

 (1.1)

: 

Доказать, что , означает найти зависимость

Пример 1.1. Доказать, что .

Доказательство. Рассмотрим неравенство .

,  , 

Для того чтобы для  выполнялось условие  достаточно выбрать .

Если то , , N=9, т.е. все члены, начиная с x₁₀, находятся в 0,01-окрестности точки 1.

                            0,99              1             1,01

Числовая последовательность, имеющая предел, называется сходящейся. Если же предел не существует или равен , то последовательность называется расходящейся.

1.3. Свойства передела

1. Предел линейной комбинации

.                  (1.2)

2. Предел произведения

.                             (1.3)

3. Предел частного

, если .             (1.4)

4. Предел отношения многочленов

Пусть x_n и y_n многочлены от n степени k и m соответственно, т.е.

x_n=P_k(n)=a₀ n^k+a₁n^k-1+...+a_k,   y_n=Q_m(n)=b₀n^m+b₁n^m-1+...+b_m, т.е.

         (1.5)

Имеем:  . Итак,

                               (1.6)

Пример 1.2. Найти пределы:

а)   б) ,  в)

Решение.

а)   

б), 

в) .

Следует отметить, что формулы (1.5) и (1.6) справедливы не только для многочленов целой степени, но и для многочленов дробной степени, так как  для любого a>0.

Пример 1.3. Найти пределы.

а) ,      б) , 

в) ,           г) , 

д) ,      е) .

Решение:

а) В числителе три слагаемых соответственно степени:  Следовательно, степень числителя равна , а главный член в числителе равен . Аналогично, главный член в знаменателе  Имеем по формулам (1.5) и (1.6):

а)

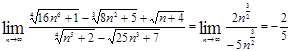
б)   

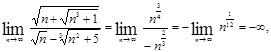
в)  

т.к.   

Здесь также можно было использовать идею, что главный член это старший член. Имеем:

г) .

Как видите, идея о главном старшем члене здесь также дает быстрое решение.

Обычно этот предел вычисляется так:

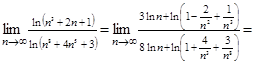
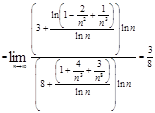
д)

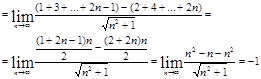
е) Напомним: .  Имеем:

Пример 1.4. (Неопределенности )

а) , 

б)         в) .

Решение. Для избавления от неопределенности  здесь следует избавиться от иррациональности в числителе, умножив и разделив данное выражение на соответствующее сопряженное выражение.

а) Используем формулу

Для данного примера

Имеем:

а)

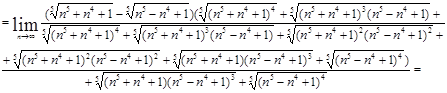
б) Напоминаем, что  и при  .

Имеем: =

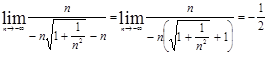
в)

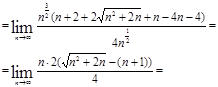
Пример 1.5. Доказать, пользуясь определением предела последовательности, что .

Решение. Имеем:

.

Решив неравенство , получим и ясно, что достаточно выбрать , чтобы для  неравенство  выполнялось для всех n>N. Что и требовалось.

2. ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ.

2.1. Определение предела функции

Число а называется пределом функции  при , если для  такое, что для , для которых , выполняется неравенство . Пишут так: .

Число а называется левосторонним пределом функции f(x) при  (слева), если для   такое, что для , для которых , выполняется неравенство .

Число а называется правосторонним пределом функции f(x) при  (справа), если для   такое, что для , для которых , выполняется неравенство .

Односторонние пределы удобно обозначать так:

Необходимое и достаточное условие существования предела с помощью односторонних пределов можно записать так:

Предел на бесконечности (при ).

Число a называется  пределом функции f (x) при  (или , если для  такое, что для , для которых , выполняется неравенство .

Пример 2.1. Доказать (найти , что:

а) ,  б)

Решение.  а) Надо доказать, что для , для которых , выполняется неравенство  для . Имеем:

Примем . Тогда .

Итак, для    такое, что  для , для которых .

б) Пусть ,

Тогда

Здесь в числителе пользуемся неравенством  а в знаменателе пользуемся неравенством .

Пусть . Тогда .

Итак, для    такое, что неравенство  выполняется для всех  x, для которых    .

2.2. Свойства предела функции

1.      Предел линейной комбинации

,

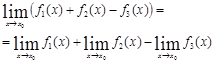
и, вообще,    .

2. Предел произведения    .

3.   Предел частного

, если пределы существуют и  .

2.3. Методы вычисления предела функции

1. Нахождение предела функции следует начинать с вычисления значения функции в точке x₀. Если f(x₀) равно конечному числу или , то предел найден. Здесь полезно пользоваться следующими символическими равенствами:, , , при a>1 ,

Пример 2.2. Найти пределы:

Чаще всего значение f(x₀) бывает неопределенным:,  ,  ,   и т. д. Рассмотрим эти неопределенности.

2.      Неопределенность  в случае отношения многочленов рассматривалась в п.1. Напомним еще раз:

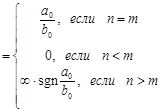   (n,m >0)

Пример 2.3. Найти пределы:

а)

б) .

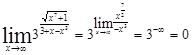3. Неопределенность . Случай отношения многочленов.

Если , то P_n(x) и Q_n(x) делятся на x-x₀. Можно числитель P_n(x) и знаменатель Q_m(x) разделить на (x-x₀) или многочлены разложить на множители и сократить множитель x-x₀.

Пример 2.4. Найти пределы:

a)

б)

Здесь применена формула

.

в)

Числитель и знаменатель должны делиться на x+2.

Имеем:

x³-2x²+16     | x+2                                x⁴+x³-x-10   |  x+2

x³+2x            x²-4x+8                   x⁴+2x³          x³-x²+2x-5

   -4x²+16                                                  -x³-x

    -4x²-8x                                                   -x³-2x²

            8x+16                                                      2x²-x

         8x+16                                        2x²+4x

                 0                                                           -5x-10

                                                                              -5x-10

                                                                                       0

Тогда,

4. Неопределенность . Случай отношения иррациональных выражений. Как правило, В этом случае стараются избавиться от иррациональности и после чего сократить множитель x-x₀.

Пример 2.5. Найти пределы

а)

б)

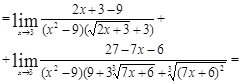
5. Неопределенность () следует преобразовать в неопределенность .

Пример 2.6. Найти пределы

а)

=.

Предел  можно свести к предыдущему с помощью замены  x=t⁶.

б)

=.

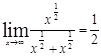6. Неопределенность .  Здесь под единицей подразумевается переменная, стремящаяся к 1, а под - переменная, стремящаяся к .

Имеется замечательный предел (второй)

  или  ,

где е - иррациональное число , основание натурального логарифма. .

Более удобным при вычислении неопределенности  являются следствия из второго замечательного предела:

,       .

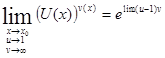Пример 2.7. Найти пределы.

а)

б)

Теорема об ограниченности функции, имеющей предел

Если функция f(x) имеет предел в точке a , то она ограниченна в некоторой окрестности точки a.

Пример:

 в окрестности точки 0.

 – не существует.

2.4 Бесконечно малые и бесконечно большие функции.

Бесконечно малой величиной при  называется функция, предел которой в точке a равен 0.

  – бесконечно малая величина (б.м.в.).

•  – бесконечно малая величина при
•  – бесконечно малая величина при

Бесконечно большой величиной при  называется функция неограниченно возрастающая.

  – бесконечно большая величина (б.б.в.)

Любая бесконечно большая величина неограниченна.

Теорема о связи предела и бесконечно малой величины

Если , то , где  – бесконечно малая величина. Или .

Пример: f(x) = x² + 1

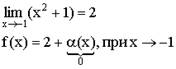
Теорема о связи бесконечно малой и бесконечно большой величиной

Если  – бесконечно малая величина при  – бесконечно большая величина.

Если – бесконечно большая величина при
 – бесконечно малая величина.

Следствие:  и

Свойства бесконечно малых величин

1) Алгебраическая сумма бесконечно малых величин есть бесконечно малая:

2) Произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая: , где f(x) – ограниченная.

3) Частное от деления бесконечно малой величины на любую функцию, предел которой не равен 0, есть бесконечно малая:  при  и .

2.5 Непрерывность функции в точке и на интервале

Определение 1. Пусть функция  определена в окрестности точки , тогда функция непрерывна в , если .

Определение 2. Функция  непрерывна, если

.

Определение 3. Функция  непрерывна в точке , если . Приращение аргумента . Приращение функции .

Определение 4. Функция  непрерывна в точке , если .Если функция не является непрерывной в точке , то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).

Определение 5. Функция  непрерывна в точке  справа, если

.

Определение 6. Функция  непрерывна в точке  слева, если

.

Функция непрерывна на отрезке , если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.

Теоремы о непрерывных функциях

Теорема 1. Сумма, произведение и частное непрерывных функций – непрерывны (кроме случая, когда знаменатель обращается в нуль).

Теорема 2. Композиция непрерывных функций непрерывна:

Функция  непрерывна в точке , если g(x) непрерывна в точке и f(y) непрерывна в .

Теорема 3. Все элементарные функции непрерывны в своей области определения.

Разрывы функции

Разрыв первого рода

Пусть  и  существуют:

I. Если , то в точке функция испытывает разрыв скачок первого рода.

Примеры:

1.                

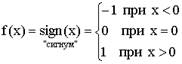
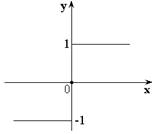
2.  – целая часть числа x.

3.  – дробная часть от числа x.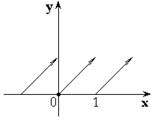

II. Если , то в точке функция испытывает устранимый разрыв первого рода.

Примеры:

1)                     

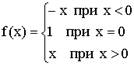
2)

3)              

4)

Разрыв второго рода

Функция испытывает разрыв второго рода, если  – не существует.

Свойства функции, непрерывной на замкнутом отрезке

Пусть функция  непрерывна на замкнутом отрезке .

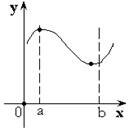
Теорема 1. Функция принимает наибольшее и наименьшее значение на .
Или , где .

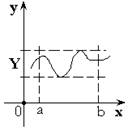
Теорема 2. Функция принимает все свои промежуточные
значения на .
Или , где  – область значений.

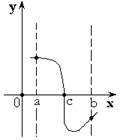Теорема 3. Если функция принимает на концах отрезка значения разных знаков, то внутри отрезка найдется точка, в которой .
Или .

Вопросы для закрепления:

1. Понятие предела функции.

2. Бесконечно малые  и бесконечно большие функции и их свойства.

3. Раскрытие неопределённости вида 0/0 и ∞/∞.

4. Замечательные пределы.

5. Понятие непрерывности функции.

6. Понятие разрывных функций и виды разрывов.

Для подготовки к самостоятельной работе:

1.        Прочитать учебник О₂: п. 6.1 – 6.7, стр. 40.

2.        Выучить лекцию

3.        Скачано с www.znanio.ru