
Для решения обратной
задачи эллипсометрии, в рамках однослойной модели часто используется метод
Малина-Ведама. Принципиальным недостатком этого метода является то, что толщина
слоя может быть определена лишь с точностью до фазовой толщины, кратной ![]() . Также метод
Малина-Ведама использует информацию о толщине заключённую только в
действительной части корней уравнения (2.25). Эти недостатки устранены в
разработанном модифицированном методе Малина-Ведама [28], который оптимизирован
для исследования сильнопоглощающих покрытий и учитывает многолистность функции
. Также метод
Малина-Ведама использует информацию о толщине заключённую только в
действительной части корней уравнения (2.25). Эти недостатки устранены в
разработанном модифицированном методе Малина-Ведама [28], который оптимизирован
для исследования сильнопоглощающих покрытий и учитывает многолистность функции
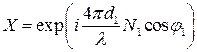 . (3.1)
. (3.1)
Суть этого метода (как и метода Малина-Ведама) состоит в графическом решении системы уравнений (2.25) для различных углов падения.
В случае, когда оптические параметры подложки известны, уравнение (2.25) имеет два корня, на которые накладывается следующее ограничение (условие затухания волны вглубь структуры):
![]() . (3.2)
. (3.2)
Толщина плёнки может быть выражена как из действительной части (3.1):
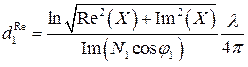 , (3.3)
, (3.3)
так и из мнимой:
![]() , (3.4)
, (3.4)
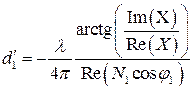 , (3.5)
, (3.5)
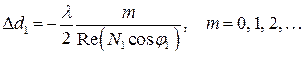 , (3.6)
, (3.6)
где ![]() – часть толщины пленки,
кратная целому числу полуволн,
– часть толщины пленки,
кратная целому числу полуволн, ![]() –
толщина пленки при
–
толщина пленки при ![]() .
Причем
.
Причем 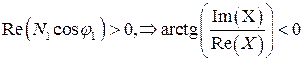 , т.е. для главных
значений
, т.е. для главных
значений ![]() ,
находящихся в интервале (
,
находящихся в интервале (![]() ;
;
![]() ), необходимо осуществить
переход в (
), необходимо осуществить
переход в (![]() ;
0).
;
0).
При переборе с некоторым
шагом всех значений ![]() и
и
![]() , для некоторого угла
падения, уравнению (2.25) удовлетворяют лишь те пары
, для некоторого угла
падения, уравнению (2.25) удовлетворяют лишь те пары ![]() ,
, ![]() , для которых верно:
, для которых верно:
![]() , (3.7)
, (3.7)
где ![]() – допустимая погрешность
выполнения условия.
– допустимая погрешность
выполнения условия.
Такие пары значений
представляются на однолистной (![]() принимает
все возможные значения) или многолистной (
принимает
все возможные значения) или многолистной (![]() ) диаграммах
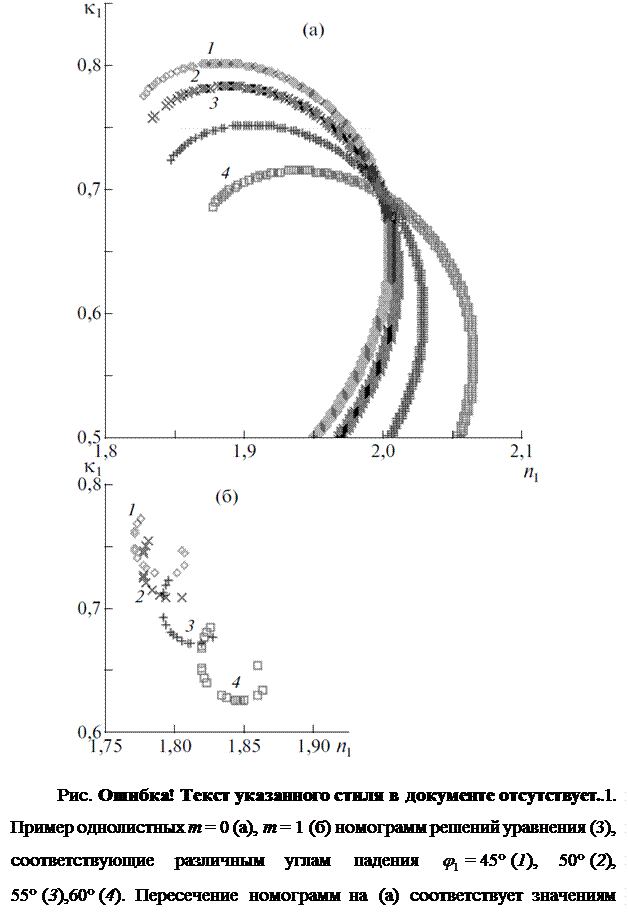
) диаграммах ![]() (Рис. 3.1). Номограммы, соответствующие различным углам падения
(Рис. 3.1). Номограммы, соответствующие различным углам падения ![]() , пересекаются в точке с
определенными значениями
, пересекаются в точке с
определенными значениями ![]() и
и
![]() , которые являются
решением обратной задачи. Соответствующая им толщина может быть найдена в
соответствии с (3.3) или (3.4).
, которые являются
решением обратной задачи. Соответствующая им толщина может быть найдена в
соответствии с (3.3) или (3.4).
Модифицированный метод
Малина-Ведама может быть использован и для изучения прозрачных покрытий (![]() ), нанесенных на
прозрачные (
), нанесенных на
прозрачные (![]() )
подложки. В этом случае отбор корней уравнения (2.25) должен удовлетворять условию
)
подложки. В этом случае отбор корней уравнения (2.25) должен удовлетворять условию
![]() , а пары значений
, а пары значений ![]() и
и ![]() связаны условием
связаны условием
![]() . (3.8)
. (3.8)
При этом истинные
значения ![]() и
и
![]() определяются
пересечением номограмм
определяются
пересечением номограмм ![]() на
на
![]() диаграмме.
диаграмме.
Следует отметить, что
решение обратной задачи эллипсометрии в случае слабопоглощающих или прозрачных
покрытий, фазовая толщина которых превышает ![]() , модифицированный метод
Малина-Ведама малоэффективен, что связано с высокими требованиями при его
использовании к точности экспериментального определения эллипсометрических
углов
, модифицированный метод
Малина-Ведама малоэффективен, что связано с высокими требованиями при его
использовании к точности экспериментального определения эллипсометрических
углов ![]() и
и ![]() .
.
Описанный метод также применим для определения эффективных параметров переходных (нарушенных) слоёв существующих на поверхностях массивных материалов.

Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.