Поделиться
151.doc
Технологическая карта урока
Предмет: Геометрия
Класс: 7
Тема урока: «Равнобедренный треугольник, свойство равнобедренного треугольника».
Учебник: «Геометрия: 7 класс» для общеобразовательных организаций /А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М. : Вентана-Граф, 2017 г
Цели для учителя: Изучение понятий равнобедренный треугольник, равносторонний треугольник и доказательство свойства равнобедренного треугольника.
Образовательные: ввести понятие равнобедренного и равностороннего треугольников; вывести и доказать свойство равнобедренного треугольника; показать применение свойства при решении задач.
Развивающие: развивать познавательные умения: сравнивать, обобщать, анализировать, систематизировать.
Воспитательные: уделить внимание эстетическому воспитанию; показать учащимся, что математика имеет свою красоту и изящество
Цели для ученика.
1. Научиться изображать, обозначать и распознавать на чертежах равнобедренные и равносторонние треугольники.
2. Формулировать и доказывать свойство равнобедренного треугольника.
3. Решать задачи с использованием свойства равнобедренного треугольника.
Тип урока: Урок открытия нового знания.
Форма урока: урок - исследование.
Планируемые результаты
Личностные:
- формирование интереса к изучении темы и желания применять приобретенные знания и умения.
- формирование умений определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать критерии для классификации
Предметные:
- Обобщение и углубление знаний учащихся о треугольниках.
- Ознакомление с понятиями равнобедренного, равностороннего, разностороннего треугольника, элементами равнобедренного треугольника
- Научится распознавать равнобедренный, равносторонний, разносторонний треугольники и изображать их.
- Умение: анализировать определение и свойства равнобедренного треугольника, применять их при решении задач
Метапредметные:
- Ответственное отношение к получению новой информации;
- способность сознательно организовывать и регулировать свою учебную деятельность;
- выработка умений работать с учебной информацией;
- умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать критерии для классификации.
- готовность к сотрудничеству с соучениками;
Понятия
Равнобедренный треугольник, равносторонний треугольник, боковые стороны и основание равнобедренного треугольника
Формы контроля: Фронтальный опрос, самопроверка, заполнение маршрутных листов
Ресурсы: Компьютер, презентация, раздаточные материалы
Структура и ход урока
|
Этап урока |
Деятельность учителя |
Деятельность ученика |
Формируемые УУД |
||||||||||||
|
1. Организационный момент |
Приветствует учеников, контролирует подготовку рабочих мест. Создает эмоциональный настрой |
Приветствуют учителя, проверяют подготовку рабочих мест |
Коммуникативные: доброжелательное отношение к окружающим. |
||||||||||||
|
2. Актуализация знаний
|
1. Фронтальная беседа - Мы изучаем тему «Треугольники». Какие новые понятия были рассмотрены на прошлом уроке? (медиана, высота, биссектриса) - дайте определение: треугольника; медианы, высоты, биссектрисы - какие инструменты необходимы для построения каждой их линий 2. Предлагает построить медиану в треугольнике 1, биссектрису в треугольнике 2, высоту в треугольнике 3 (на выданных листах 6 треугольников) 3. Контролирует выполнение задания 4. Предлагает разделить треугольники на 3 группы. (на листах 6 треугольников) 5. Какую классификацию треугольников вы использовали при выполнении задания (Классификация по углам ) 6. Сформулируйте - определения остроугольного треугольника; прямоугольного, тупоугольного 7. Результат обсуждения Демонстрация слайда 1.Классификация треугольников по сторонам.
|
1.Отвечают на вопросы, делают выводы. 2. Выполняют построения
5. Отвечают на вопросы Формулируют выводы |
Коммуникативные: -умение выражать свои мысли; -отстаивать свою точку зрения. Регулятивные: -выдвигать версии; -прогнозировать. Познавательные: -сопоставлять характеристики объектов по одному или нескольким признакам; - выявлять сходство и различие объектов. Личностные: - умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи |
||||||||||||
|
3. Изучение нового материала.
|
1.Предлагает разделить треугольники на 3 группы. По сторонам (на выданных листах 6 треугольников) Использовать при этом измерительную линейку. Сформулировать признак. Организует проверку проведенной классификации 2. Сообщает -Нас будут интересовать треугольники, у которых две стороны равны или три стороны равны Как называются эти треугольники. Предположите. Найдите подтверждение предположениям в тексте учебника 3. Записывает тему урока на доске 4. На слайде 2. вопросы для работы с учебником. Слайд 2 1.Какой треугольник называется равнобедренным? 2.Как называются равные стороны? 3. Как называется третья сторона треугольника Итог исследования предлагает оформить в таблице (приложение 1.)
5. Организует практическую работу. Проведем исследование (Научиться исследовать, значит самостоятельно узнавать новое.) Задание: Измерьте углы равнобедренного треугольника и выдвиньте гипотезу. ( работа с треугольниками 2,3,5) Направляет работу учащихся, помогает найти нужную информацию.
6. Организует обсуждение. Подводит ребят к выдвижению гипотезы. Подводит итог работы Гипотеза на слайде 3 (У равнобедренного треугольника углы при основании равны)
7. Проверили опытным путем только на трех треугольниках. Математика наука точная, чтобы утверждать, надо доказать. Еще Леонардо да Винчи говорил « Ни одно человеческое исследование не может назваться истинной наукой, если оно не прошло через математические доказательства» Физкультминутка. Координирует, направляет работу учащихся при доказательстве свойства.
8. Наше предположение подтвердилось строгим доказательством. На столах имеются тексты с исторической справкой об истории открытия равнобедренного треугольника. (Приложение 3) На доске имеется портрет Фалеса Милетского. |
1.Выполняют работу на листе с треугольниками. Номер каждого относят к одной из трех групп. Формулируют признак, которым пользуются. (Работа в парах) Обсуждают и делают выводы. Аргументируют свой выбор.
2.Читают п.23, стр. 31 и находят ответы на вопросы.
3.Записывают тему урока в тетрадях 4. отвечают на вопросы на слайде 3. Называют боковые стороны и основание изображенных на листе равнобедренных треугольников Работа с приложением 1.
5.Практическая работа. На листе 1 имеются равнобедренные треугольники. Измеряют углы при основании этих треугольников и заполняют таблицу. Результат работы в таблице
6. Формулируют гипотезу. Гипотеза. У равнобедренного треугольника углы при основании равны.
7.Доказывают гипотезу. Теорему Дано: ∆ ABC –равнобедрен., Доказать: Ð А= Ð В Доказательство: ∆ABC – равнобедренный, значит СА = СВ СВ = СА Ð С – общий, значит по первому признаку равенства треугольников, ∆АСВ =∆ ВСА , следовательно Ð А= Ð В
8. Читают текст «О равнобедренном треугольнике. Фалес Милетский». Отвечают на вопросы: 1.В какой стране развивалось учение о треугольниках? 2.Какой ученый занимался изучением равнобедренного треугольника? 3.Научные достижения Фалеса Милетского. |
Предметные: Научиться находить равнобедренные треугольники. Познавательные: -читать и извлекать нужную информацию; -умение работать с текстом. Регулятивные: -выдвигать версии; -прогнозировать. -анализировать Коммуникативные: -умение точно и полно излагать свои мысли. Предметные: Научиться находить боковые стороны и основание треугольников.
Познавательные: -умение работать с транспортиром; -представлять информацию в виде таблиц. Коммуникативные: -умение выслушивать членов команды, не перебивая; принимать коллективные решения. Личностные: -формирование навыков коллективного проектирования.
Регулятивные: -формулировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций.
Познавательные: -читать и извлекать нужную информацию; -умение работать с текстом. Познавательные: - умения перерабатывать полученную информацию, делать выводы в результате индивидуальной работы. |
||||||||||||
|
4. Решение практических задач (закрепление пройденного материала). |
1.Организует работу в группах. Любое исследование должно иметь практическое применение. 2. Направляет работу учащихся. 3. Запишите в тетрадях главный вывод задачи.
|
1. Решают практические задачи на готовых чертежах. Найти угол АВD. Приложение 2.
Для тех, кто решит. Работа над задачей №12, стр.31 учебник. Самостоятельный разбор задачи.
|
Коммуникативные: - умение оформлять свою мысль в учебной речи; - грамотно формулировать высказывания. Предметные: -научится применять теорему о свойствах углов равнобедренного треугольника. Регулятивные: - умения выполнять учебные действия в соответствии с планом. |
||||||||||||
|
5. Проверка изученного. |
-Мы славно потрудились на уроке, узнали много нового. Хотелось бы узнать, как вы усвоили материал урока. У меня в руках два листа бумаги. На одном изображен разносторонний треугольник, а на другом равнобедренный. Задайте мне только один вопрос и выслушав ответ, скажите, какой треугольник на каком листе изображен? |
Задают вопросы. |
Познавательные: -уметь устанавливать причино-следственные связи. |
||||||||||||
|
6.Рефлексия. |
1. Оцените свою работу. |
Оценивают работу в баллах. 10б. – все понял 8б. – все понял, но затрудняюсь в решении задач. 6б. – понял не все. 4б. – ничего не понял |
Познавательные: - давать оценку действиям, оценивать результат. |
||||||||||||
|
7. Итог урока и домашнее задание.
|
1.Комментирует домашнее задание |
Записывают домашнее задание. П.23, №9,10.стр.39. Ответить на вопрос «Где применяются равнобедренные треугольники в жизни?» |
Познавательные: - находить ответы, используя свой жизненный опыт и информацию, полученную на уроке. |
Приложение 1.
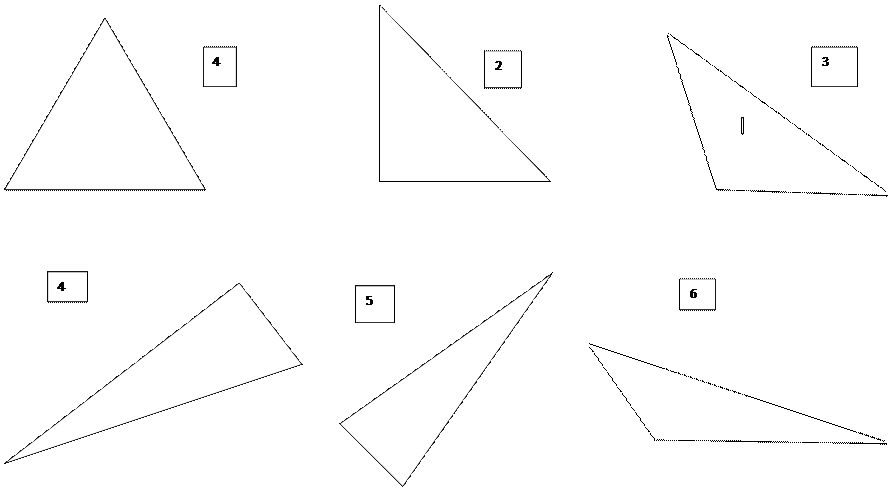Классификация ………….. ( по углам)
|
Классификация ………….. ( по углам) 1) 2) 3) |
Классификация ………… ( по сторонам) 1) 2) 3) |
|||||
|
№ |
Углы |
Вид треугольника |
Стороны |
Вид треугольника |
Вид треугольника По двум признакам |
|
|
1 |
Три острые |
Остроугольный треугольник |
Три стороны равны |
равносторонний треугольник |
|
|
|
2 |
1 угол прямой |
Прямоугольный треугольник |
Две стороны равны |
равнобедренный треугольник |
|
|
|
3 |
1 угол тупой |
Тупоугольный треугольник |
Две стороны равны |
равнобедренный треугольник |
|
|
|
4 |
1 угол прямой |
Прямоугольный треугольник |
Все стороны разной длины |
разносторонний треугольник |
|
|
|
5 |
Три острые |
Остроугольный треугольник |
Две стороны равны |
равнобедренный треугольник |
|
|
|
6 |
1 угол тупой |
Тупоугольный треугольник |
Все стороны разной длины |
разносторонний треугольник |
|
|
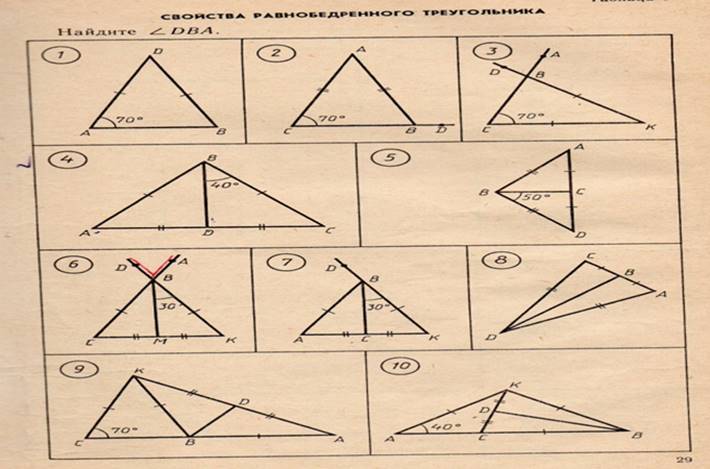Приложение
2.
Приложение 3.
историческая справка об истории открытия
равнобедренного треугольника
Фалес Милетский из Милета, ионийского города на западном побережье Малой Азии, который был основан греками. Он считается родоначальником греческой философии и науки. Как философ, он учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее в конце концов опять превращается. Историческое значение философской деятельности Фалеса заключается в том, что им был сделан решающий шаг от мифологического мировоззрения к научному материалистическому представлению о мире.
Почти все философы Древней Греции тщательно занимались математикой, и в частности, геометрией. Фалесу Милетскому Прокл приписывает открытие или доказательство теорем о том, что: углы при основании равнобедренного треугольника равны, диаметр делит круг пополам, вертикальные углы равны и др. Эти положения были частично известны еще вавилонянам и египтянам. Однако в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае.
При помощи общих доказательств, с постепенным переходом от одной истины к другой, греческие математики создали геометрию как науку. Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионийской школы, основателем которой и был Фалес.
Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и и.п. Особенную славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Фалес был не только философом и ученым, но также государственным и общественным деятелем. Вот почему он был причислен к группе “семи мудрецов” древности.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
