Начало анализа

                                                                Эпиграф урока:

                                                                         Математику нельзя изучать,

                            наблюдая, как это делает сосед!

                                            А.Нивен.

        Тема: Раскрытие скобок.

Цель урока: Научить раскрывать скобки перед которыми стоит знак + или -,

умножать алгебраическую сумму на число.

Задачи:  

1. Повторить и закрепить правила преобразования буквенных выражений, определение числового коэффициента и правила сокращения дробей;

2.Объяснить правила раскрытия скобок и значение скобок в выражениях. В течение урока развивать у учащихся навык раскрытия скобок.

3.Воспитание навыков самостоятельной работы.

 

Ход урока

I. Организация обучающихся.

II. Проверка домашнего задания, актуализация знаний

Выяснить выполнение домашнего задания, собрать тетради.

Устные упражнения.

Вычислите:

•      -5 + (-7)

•      -23 + (-59)

•      -9 + 4

•      19,17 + (-12,07)

•      15 – 17

•      -13,2 – (-13,7)

 

1.     - 70: 10  = 

2.     60: (-2)  =

3.     - 160 + 40 =

4.     - 300: (-100) =

5.     (-90) + (- 909)=

6.     - 150 + 400 =

7.     - 90 + 125 =

8.     -0,125 ∙ 4x (-8) =

Упростите выражение и назовите коэффициент.

3x· 5y=

-25 а· 4вс=

0,1вс· 20а=

 

 Упростите выражение:

38 + в – 45

а -3 +3

-5 -7 – с

 

IV. Работа по карточкам

Упростите выражение:

1. z · (-y) ·  (-x)

2        5а·(-2в) · 7с

3. – 1,2 авс · 4,5а

Найдите  неизвестный член пропорции:

 

V.  Мотивация «открытия» новой информации

Рассказ Кужабековой об истории алгебры.

 Основоположником алгебры, как особой науки нужно считать среднеазиатского ученого Мухаммеда из Хорезма, известного под арабским прозвищем Аль-Хоризми (Хорезмиенец). Его алгебраический труд, составленный в 9 в. н. э., носит название "Книга восстановления и противопоставления". "Восстановлением" Мухаммед называет перенос вычитаемого из одной части уравнения в другую, где оно становится слагаемым; "противопоставлением" - собирание неизвестных в одну сторону уравнения, а известных - в другую сторону. На арабском языке "восстановление" называется "ал-джебр". Отсюда и название "алгебра".
Вспомним основные свойства :

a +b = b + a

a · b = b · a

a ·(b+c) = ab +ac            распределительное свойство

a – (b+c) = a – b - c

a – (b- c) = a – b + c

 

VI. Изучение новой темы

Пример 1.

Выполните действия:

-3,78 + (3,78 – 6,73)

2 способ:

Уберите скобки и вычислите: -3,78 + 3,78 – 6,73

 

Пример 2

2а + (3в – с) = 2а + 3в + (-с) = 2а + 3в - с

Вывод:

Чтобы к некоторому выражению прибавить алгебраическую сумму, надо прибавить к этому выражению отдельно каждое слагаемое этой суммы.

 

Рассмотрим следующий пример:

9 – (7 – 6) = 9 – 7 + 6

 а – (в – с) = а – в +с

 

 

Вывод: Чтобы из некоторого выражения вычесть алгебраическую сумму, надо прибавить к нему отдельно каждое слагаемое этой суммы, взяв его с противоположным знаком.

 а – (-в +с) + (с –в) = 

 

-(а – в + с)=

 

•      Если перед скобкой минус,

Он ведет себя, как вирус.

Скобки сразу все съедает,

Всем, кто в скобках, знак меняет.

 

•      Ну, а если плюс стоит,

Он все знаки сохранит

 

Пример 3

5 (а + 2с) =

-5а (3с – 6в) =

Вывод: Чтобы умножить некоторое выражение на алгебраическую сумму, нужно умножить это выражение отдельно на каждое слагаемое суммы и результаты сложить.

Физминутка

 

VII. Первичное закрепление с проговариванием правил.

 

 № 282

№ 292

№ 294

 

Самостоятельная работа с самопроверкой по образцу.

 

Вариант 1

1. а) а + b + ( р – с) = а + b +  р – с

 б)  m – ( x – p + n ) = m –  x + p - n

2. a)  8,3 + ( 4,5 – 6,3) = 8,3 +  4,5 – 6,3 = 6,5

   б) 4,1 – ( 5,6 – 6,9) = 4,1 –  5,6 + 6,9 = 5,4

 

Вариант 2

1. а)k + ( a – b ) + n = k +  a – b  + n

   б) x – ( m + y – n ) = x –  m  -   y + n

2. а) 5,94 + ( 7,2 – 4,14 ) = 5,94 +  7,2 – 4,14 = 9

 б) 8,31 – ( 7,2 – 1,89) = 8,31 – 7,2 + 1,89 = 3

VIII.  Осмысление изученного и сделанного

 Как из некоторого выражения вычесть алгебраическую сумму?

 Как к выражению прибавить алгебраическую сумму?

  Как число умножить на алгебраическую сумму?

 

IX. Информация о домашнем задании, инструктаж по его выполнению.

Стр 78-80

№285

№ 293

X. Рефлексия

Поговорки – зеркало настроения

1. Смелость города берет

2. Старая песня на новый лад;

3. О, монах, ты идешь трудной дорогой;

4. Ах, как я устал от этой суеты:

5. Без труда не вытащишь рыбку из пруда.

 

 

 

 

 

 

Вариант 1

1.

 а) а + b + ( р – с) =

 б)  m – (x – p + n ) =

2.

a)  8,3 + (4,5 – 6,3) =

   б) 4,1 – (5,6 – 6,9) =

  3.

 22(в - 100 – 4а) =

   - 33(2х – ху + 3у) =

 

 

Вариант 2

1.

а)k + (a – b ) + n =

   б) x – (m + y – n ) =

2.

 а) 5,94 + (4,8 – 4,14 ) =

 б) 8,31 – (7,2 – 1,89) =

  3.

- 9(8 + х – 4у) =

18(- а - в + с) =

 

 

 

 

•      Если перед скобкой минус,

Он ведет себя, как вирус.

Скобки сразу все съедает,

Всем, кто в скобках, знак меняет.

 

•      Ну, а если плюс стоит,

Он все знаки сохранит

 

 

Упростите выражение:

1.    z · (-y) ·  (-x)

2.         5а·(-2в) · 7с

3. – 1,2 авс · 4,5а

 

 

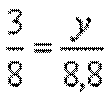
Найдите  неизвестный член пропорции: