
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 1 р.п. Мокшан
Исследовательская работа
по математике
«Методы решения тригонометрических уравнений и способы отбора корней на заданном промежутке»
Выполнил: Васякин Михаил, ученик 11 класса
МБОУ СОШ №1 р.п. Мокшан
Научный руководитель:
Паркина Наталья Ивановна,
учитель математики
МБОУ СОШ №1 р.п. Мокшан
2018 год
Содержание
Глава I. О тригонометрических уравнениях и основных методах их решения.
I. Общие правила решения тригонометрических уравнений:
Применение методов в практике по решению тригонометрических уравнений
1 метод: Разложение одной из частей уравнения на множители.
2 метод: Замена переменной.
3 метод: Применяется к однородным тригонометрическим уравнениям.
4 метод: Решение уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.
5 метод: Метод подстановки.
6 метод: Решение тригонометрических уравнений, содержащих обратные тригонометрические функции.
7 метод: Метод универсальной подстановки.
8 метод: Функционально-графический способ
9 метод: Решение тригонометрических уравнений с параметрами.
Глава II. Приемы отбора корней в тригонометрических уравнениях
Глава III. Уравнения, предлагавшиеся на ЕГЭ.
Заключение
Приложение 1
Приложение 2
Список использованной литературы
Введение
«Уравнения для меня важнее,
потому что политика — для настоящего,
а уравнения — для вечности»
Альберт Эйнштейн
Тригонометрические уравнения одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий централизованного тестирования.
Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях конечное число корней, а в тригонометрических – бесконечное, что сильно усложняет отбор корней. Еще одной особенностью тригонометрических уравнений является неединственность формы записи ответа.
Долгое время тригонометрию рассматривали как раздел геометрии, и это порождало у школьников неверное представление о тригонометрических функциях, границы применимости которых, к тому же, сводились до минимума.
В настоящее время тригонометрию изучают в курсе алгебры и начал анализа, хотя основное понятие тригонометрической функции в учебной литературе по-прежнему задается геометрическим способом в виду отсутствия у старшеклассников знаний теории рядов. Таким образом, изучение тригонометрических функций, а в дальнейшем и тригонометрических уравнений, в школьном курсе имеет некоторые особенности.
При изучении тригонометрических уравнений в общеобразовательной школе не хватает времени на рассмотрение уравнений, решаемых нетрадиционными способами. Поэтому мне стало интересно рассмотреть решения таких уравнений, тем более такие уравнения я встречал в олимпиадных заданиях и эти знания мне пригодятся в дальнейшем.
С точки зрения стандартных школьных методов решения тригонометрических уравнений, рассмотрю новые методы, не изучаемые в школьном курсе. Заинтересовавшись темой решения тригонометрических уравнений, я самостоятельно стал пробовать решать уравнения из сборников по математике повышенной сложности, сборников олимпиадных задач и понял, что моих знаний не хватает для решения многих типов тригонометрических уравнений. Постараюсь как можно лучше раскрыть методы решения тригонометрических уравнений путем приведения решений таких уравнений.
Процесс нахождения решений тригонометрического уравнения состоит из двух основных этапов: преобразования уравнения до получения простейшего (их системы либо совокупности) и решения последнего (или последних).
В зависимости от вида исходного тригонометрического уравнения, существуют различные методы их решения, и в данной работе подробно рассматривается каждый из них, сопровождается примерами из вступительных экзаменов и пособий для абитуриентов.
Актуальность темы заключается в том, что тригонометрические уравнения включены во вторую часть Единого Государственного Экзамена. Задания такого плана содержат две части: непосредственное решение уравнения, в результате которого получается бесконечное множество корней, и последующий отбор корней на предмет принадлежности конкретному промежутку. Новизна исследования состоит в том, что показана возможность эффективного решения отдельных тригонометрических уравнений.
Актуальность темы определяется тем, что учащиеся должны разбираться в тех или иных способах решения тригонометрических уравнений и уметь правильно отбирать нужные корни.
Поэтому, перед собой я поставил следующую цель:
Систематизировать, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений и способов отбора корней в тригонометрических уравнениях.
Объектом исследования является изучение тригонометрических уравнений в заданиях ЕГЭ.
Предмет исследования - решение тригонометрических уравнений и способы отбора корней в тригонометрических уравнениях.
В соответствии с целями, объектом и предметом исследования определены следующие задачи:
1. Рассмотреть различные типы заданий, содержащие тригонометрические уравнения, предлагавшиеся на ЕГЭ работ предыдущих лет и при выполнении диагностических работ, где необходимо выполнить отбор корней, классифицировать их;
2. Определить наиболее рациональный способ отбора корней для каждого типа заданий;
3. Рассмотреть рекомендации по решению тригонометрических уравнений из вариантов ЕГЭ;
4. Составить презентацию полученных результатов. Сделать выводы.
При выполнении работы использовались материалы ЕГЭ по математике. Основные источники получения информации: официальные документы, научная и справочная литература.
Определение 1. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Простейшие тригонометрические уравнения - это уравнения вида sin x = a,
cos x=a, tg x=a, ctg x = a.
В таких уравнениях переменная находится под знаком тригонометрической функции, а - данное число.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения.
Для решения тригонометрических уравнений используется несколько основных формул, около 20 дополнительных, и всего 8 методов решения. Все эти методы по-своему хороши и применимы для разных видов тригонометрических уравнений. Главная задача при решении тригонометрического уравнения состоит в том, чтобы правильно преобразовать его, свести к какому-нибудь более стандартному варианту подобрать наилучший способ решения для конкретного случая. То есть, в большинстве своём, главная проблема заключается в том, что уравнения надо непременно сначала привести к какому-то виду, прежде чем применить нужный метод решения.[1]
Итак, основных методов решения тригонометрических уравнений 8:
1) Разложение одной из частей уравнения на множители.
В данном случае мы все слагаемые переносим в левую часть, раскладываем её на множители и приравниваем каждый множитель к нулю.
Недостаток метода: может быть применён только к узкому кругу уравнений.
2) Замена переменной.
В данном случае уравнение приводят к такому виду, чтобы остался только один вид тригонометрической функции, а затем заменяют её на новую переменную. После решения уравнения относительно введённой переменной, остаётся только решить получившиеся простейшие тригонометрические уравнения согласно базовым формулам.
Преимущество метода: может быть применён к любому тригонометрическому уравнению (если только это целесообразно), так как все тригонометрические функции можно выразить друг через друга. Может также применяться совместно с другими методами.
Недостаток метода: Иногда, пытаясь свести всё уравнение к одному типу тригонометрической функции, мы получаем слишком сложное уравнение, так как не все функции связаны простыми зависимостями. К тому же метод нецелесообразен, когда в уравнении много разных тригонометрических функций.
3) Метод решения однородных тригонометрических уравнений.
В данном случае мы сначала приводим уравнения к однородному тригонометрическому уравнению. Затем делим обе части на cos x/cos2x/cos3x в зависимости от степени уравнения. Затем производим замену переменной и решаем методом замены переменной.
Преимущество метода: очень прост в применении. Одинаков для всех тригонометрических уравнений одной степени.
Недостаток метода: Далеко не все тригонометрические уравнения можно привести к виду однородных.
4) Решение уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.
Недостаток метода: можно решить только уравнения определённого вида или сводимые к ним уравнения.
5) Метод подстановки.
В этом случае вместо часто повторяющейся разности или суммы двух функций подставляют переменную, решают уравнение относительно неё, а затем возвращаются к сумме или разности функций, которая была заменена.
Преимущество метода: даёт большие результаты в комплексном использовании вместе с другими методами.
Недостаток метода: редко применим к сложным уравнениям.
6) Решение тригонометрических уравнений, содержащих обратные тригонометрические функции.
7) Метод универсальной подстановки.
При
решении тригонометрических уравнений можно использовать и так называемую
универсальную тригонометрическую подстановку на основе формул: 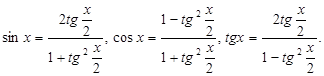
Если
теперь ввести обозначение ![]() то
то ![]()
С
помощью универсальной подстановки мы можем любое уравнение вида ![]() свести к алгебраическому
уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те
корни исходного уравнения, для которых
свести к алгебраическому
уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те
корни исходного уравнения, для которых ![]() не определён, то есть значения
не определён, то есть значения ![]() их мы должны проверять
отдельно.
их мы должны проверять
отдельно.
Преимущество: применим для большинства уравнений. В сопряжении с другими методами едва ли не уникален.
Недостаток: после применения подстановки сужается область определения уравнения, поэтому все значения необходимо проверять.
8) Ограниченность функций (графический способ).
Каждая часть уравнения рассматривается как отдельная функция, причём первая из них – тригонометрическая, а вторая – алгебраическая, строятся графики этих функций, находятся их пересечения.
Преимущество метода: Наглядность, отсутствие сложных преобразований.
Недостатки: Невозможность построения некоторых графиков. Возможность неточностей в определении координат точек пересечения. Возможность ошибки в построении.[2]
*9) Решение тригонометрических уравнений с параметрами.
Также существуют общие правила решения тригонометрических уравнений. Во время решения необходимо решать задачи:
1) отсева посторонних корней,
2) потери корней,
3) пересечения решений.
Решение тригонометрических уравнений сводится, как правило, к решению простейших уравнений:
a) sin x = a.
Все решения можно описать формулой:
x = (-1)k arcsin a + πk, где k – число целое.
b) cos x = a.
Все решения можно описать формулой:
x = ![]() arccos a + 2πk, где k –
число целое.
arccos a + 2πk, где k –
число целое.
c) tg x = a.
Все решения можно описать формулой:
x = arctg a + πk, где k – число целое.
d) ctg x = a.
Все решения можно описать формулой:
x = arcсtg a + πk, где k – число целое.
Если a = 0,-1,1 то для решения уравнений используются следующие частные формулы:
sin x = 0, x = πk, где k – число целое.
sin x = 1, x = ![]() +2πk, где k –
число целое.
+2πk, где k –
число целое.
sin x = -1, x = -![]() + 2πk, где k –
число целое.
+ 2πk, где k –
число целое.
cos x = 0, x = ![]() +πk, где k –
число целое.
+πk, где k –
число целое.
cos x = 1, x = 2πk, где k – число целое.
cos x = -1, x = π +πk, где k – число целое.
tg x = 0, x = πk, где k – число целое.
ctg x = 0, x = ![]() +πk, где k –
число целое.
+πk, где k –
число целое.
При данном методе решения всё переносится в левую часть уравнения так, чтобы в правой при этом оставался 0. Затем левая часть уравнения раскладывается на множители и далее уравнение решается согласно известному правилу: если произведение равно нулю, значит хотя бы один из множителей равен нулю. Так мы получаем из сложного уравнения совокупность простых уравнений вида cos t = a, sin t = a, tg t = a, ctg t = a, для решения которых используются указанные формулы.[3]
Примеры применения данного метода:
4sin
t![]() cos
t – 2cos t + 2sin t - 1 = 0
cos
t – 2cos t + 2sin t - 1 = 0
(2sin t – 1)(2cos t + 1) = 0
2sin t – 1 = 0 или 2cos t + 1 = 0
sin
t = ![]() или
cos t = -
или
cos t = - ![]()
Тогда:
t = (-1)к![]() arcsin
arcsin ![]() + πk, k – число целое
или
+ πk, k – число целое
или
t = ![]() arcos(-
arcos(-![]() ) a + 2πk, где k – число целое.
) a + 2πk, где k – число целое.
Иначе:
t = (-1)к ![]()
![]() + πk, k – число целое
или
+ πk, k – число целое
или
t = ![]() + 2πk, где k – число
целое.
+ 2πk, где k – число
целое.
3tg2 t – 2tg t = 0
tg
t![]() (3tg t – 2) = 0
(3tg t – 2) = 0
tg t = 0 или 3 tg t – 2 = 0
tg
t = 0 или tg t = ![]()
Тогда:
t = arctg 0 + πk = πk, где k – число целое или
t = arctg ![]() + πk, где k – число целое.
+ πk, где k – число целое.
![]() ctg t = ctg3
t
ctg t = ctg3
t
![]() ctg t – ctg3
t = 0
ctg t – ctg3
t = 0
ctg
t![]() (
(![]() – ctg2 t) = 0
– ctg2 t) = 0
ctg
t![]() (
(![]() – ctg t)
– ctg t)![]() (
(
![]() +
ctg t) = 0
+
ctg t) = 0
ctg
t = 0 или
![]() –
ctg t = 0 или
–
ctg t = 0 или ![]() + ctg t = 0
+ ctg t = 0
Тогда:
t = ![]() + πk, k – число целое.
+ πk, k – число целое.
t = arcctg ![]() + πk, где k– число целое
+ πk, где k– число целое
t = (π– arcctg ![]() ) + πk, где k –
число целое.
) + πk, где k –
число целое.
1
– sin x![]() cos
x = sin x – cos x
cos
x = sin x – cos x
1
– sin x![]() cos
x – sin x + cos x = 0
cos
x – sin x + cos x = 0
(sin
x -1) + cos x![]() (sin x – 1) = 0
(sin x – 1) = 0
(cos
x + 1)![]() (sin
x – 1) = 0
(sin
x – 1) = 0
cos x + 1 = 0 или sin x – 1 = 0
cos x = -1 или sin x = 1
x 1 =π + πk, где k– число целое.
x 2 = ![]() + 2πn, где n –
число целое.
+ 2πn, где n –
число целое.
При данном методе решения также все слагаемые переносятся в левую часть, в правой остаётся 0, а тригонометрическая функция в уравнении заменяется переменной. Далее уравнение решается как обычное квадратное уравнение относительно этой переменной. После нахождения значений необходимо заменить переменную соответствующей тригонометрической функцией и найти корни исходного уравнения по формулам.
Примеры применения данного метода:
1) 3cos2 x = 7(sin x +1)
3 – 3sin2 x – 7sin x – 7 = 0
3sin2 x + 7sin x + 4 = 0
Пусть sin x = a, тогда:
3a2 + 7a + 4 = 0
D = 49 – 4*12 = 1
a 1 = ![]() = -1
= -1
a 2 = ![]() =
= ![]() =
= ![]() , посторонний корень.
, посторонний корень.
Т.к. a = sin x, то:
sin x = -1
x = (-1)k+1 * arcsin1 + πk, k – число целое.
x = (-1)k+1 * ![]() + πk, k – число
целое.
+ πk, k – число
целое.
2) tg2 x + 2tg x – 3 = 0
Пусть tg x = a, тогда:
a2 + 2a – 3 = 0
D = 4 + 12 = 16 = 42
а
1 = ![]() = 1
= 1
a
2 = ![]() = -3
= -3
Т.к a = tg x, то:
tg x = -3 или tg x = 1
x
= -arctg 3 + πk
или x = ![]() + πk,
где k – число целое.
+ πk,
где k – число целое.
3)
![]() +
10 =
+
10 = ![]() +
7
+
7
2ctg2 x + 10 + 5ctg x – 7 = 0
2ctg2 x + 5 ctg x + 3 = 0
Пусть ctg x = a, тогда:
2a2 + 5a + 3 = 0
D
= 25 – 4![]() 2
2![]() 3
= 1
3
= 1
a1
= ![]() =
-1
=
-1
a2
= ![]() =
-1.5
=
-1.5
Т.к. a = ctg x, то:
ctg x = -1 или ctg x = - 1.5
x = π – arcctg1 + πk или x = π – arcctg1.5 + πk, где k – число целое.
x =![]() + πk или x
= π – arcctg1.5 + πk, где k – число целое.
+ πk или x
= π – arcctg1.5 + πk, где k – число целое.
4)![]()
Перепишем уравнение в
виде ![]() получили
уравнение, однородное относительно
получили
уравнение, однородное относительно ![]() и
и ![]() Рассмотрим два случая:
Рассмотрим два случая:
1)![]() тогда
тогда ![]() откуда
откуда![]() что невозможно, поскольку
что невозможно, поскольку ![]() в этом случае корней нет.
в этом случае корней нет.
2)![]() тогда разделим обе части
уравнения на
тогда разделим обе части
уравнения на ![]()
![]() Пусть
Пусть ![]() Получим
Получим ![]() откуда
откуда ![]() Осталось решить уравнения
Осталось решить уравнения ![]() и
и ![]()
Ответ: ![]() где
где ![]()
Определение однородных тригонометрических уравнений:
Уравнение вида asin x + bcos x = 0 называют однородным тригонометрическим уравнением первой степени.
Уравнение вида a![]() sin2 x + b
sin2 x + b![]() sin x
sin x![]() cos x+ ccos2 x = 0 называют
однородным тригонометрическим уравнением второй степени.
cos x+ ccos2 x = 0 называют
однородным тригонометрическим уравнением второй степени.
Уравнение вида a![]() sin3 x + b
sin3 x + b![]() sin2 x
sin2 x![]() cos x+ c
cos x+ c![]() sin x
sin x![]() cos2 x + d
cos2 x + d![]() cos3 x = 0 называют однородным
тригонометрическим уравнением третей степени.
cos3 x = 0 называют однородным
тригонометрическим уравнением третей степени.
А вообще тригонометрическое уравнение называют однородным, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени.
1)Однородные тригонометрические уравнения первой степени решают так:
Сначала обе части уравнения делим почленно на cos x, получим:
a![]() sin
x + b
sin
x + b![]() cos
x = 0
cos
x = 0 ![]()
![]() +
+ ![]() =
= ![]()
Выполнив преобразования, получим:
a![]() tg x + b = 0
tg x + b = 0
tg x =![]()
Отсюда по формуле находим x.
2)Однородные тригонометрические уравнения второй степени решают так:
a![]() sin2
x + b
sin2
x + b![]() sin
x
sin
x![]() cos
x+ c
cos
x+ c![]() cos2
x = 0
cos2
x = 0 ![]() cos2 x
cos2 x
![]() +
+ ![]() +
+ ![]() =
= ![]()
Выполнив преобразования, получим:
аtg2 x + btg x + c = 0
Далее решаем уравнение методом замены переменной.(см. пример 4) к этому методу).
3)Однородные тригонометрические уравнения третей степени решают так:
a![]() sin3
x + b
sin3
x + b![]() sin2
x
sin2
x![]() cos
x+ c
cos
x+ c![]() sin
x
sin
x![]() cos2
x + d
cos2
x + d![]() cos3
x = 0
cos3
x = 0 ![]() cos3 x
cos3 x
![]() +
+![]() +
+ ![]() +
+ ![]() = 0
= 0
Выполнив преобразования, получим:
a![]() tg3
x + b
tg3
x + b![]() tg2
x + c
tg2
x + c![]() tg
х+
d = 0
tg
х+
d = 0
Далее производим замену переменной и решаем получившееся кубическое уравнение относительно новой переменной. Затем возвращаемся к замене и вычисляем по формуле корни уравнения.
Примеры применения данного метода:
sin2
x + 2 sin(π– x) ![]() cos
x – 3cos2 (2π
– x) = 0
cos
x – 3cos2 (2π
– x) = 0
Выполнив преобразования, получим:
sin2
x + 2sin x![]() cos x – 3cos2
x = 0
cos x – 3cos2
x = 0 ![]() cos2 x
cos2 x
![]() +
+ ![]() -
- ![]() =
= ![]()
tg2 x + 2tg x – 3 = 0
![]() Получаем
уравнение, уже решённое нами как пример 2 ко второму методу решения тригонометрических
уравнений.
Получаем
уравнение, уже решённое нами как пример 2 ко второму методу решения тригонометрических
уравнений.
2)
3sin 2 3x - √2 3 sin3x![]() cos3x + 5cos2
3x = 2
cos3x + 5cos2
3x = 2
Данное уравнение не является
однородным уравнением, поэтому сначала его необходимо привести к виду a![]() sin 2 x +
bsinx
sin 2 x +
bsinx![]() cos x+ c
cos x+ c![]() cos 2 x = 0.
cos 2 x = 0.
sin 2 t + cos 2 t = 1
Тогда 2sin 2 t + 2cos 2 t = 2. Заменим t на 3x. Получим равенство:
2sin 23x + 2cos2 3x= 2
Подставим выражение из левой части в правую часть исходного уравнения. Получим:
3sin2
3x - 2![]() sin3x
sin3x![]() cos3x
+ 5cos2 3x = 2sin 23x + 2cos 23x
cos3x
+ 5cos2 3x = 2sin 23x + 2cos 23x
3sin2
3x - 2![]() sin3x
sin3x![]() cos3x
+ 5cos2 3x – 2sin 23x – 2cos 23x = 0
cos3x
+ 5cos2 3x – 2sin 23x – 2cos 23x = 0
sin2 3x - 2![]() sin3x
sin3x![]() cos3x
+ 3cos2 3x = 0
cos3x
+ 3cos2 3x = 0 ![]() cos2 3x
cos2 3x
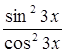 -
- 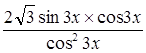 +
+
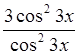 =
=
![]()
tg2
3x – 2![]() tg3x
+ 3 = 0
tg3x
+ 3 = 0
Пусть z = tg3x, тогда:
z2
– 2![]() z
+ 3 = 0
z
+ 3 = 0
(z-![]() )
2 = 0
)
2 = 0
z
=![]() ,
т.е.
tg 3x =
,
т.е.
tg 3x =![]()
Тогда по формуле
3x = arctg![]() + πk
+ πk
3x = π/3 + πk
x = π/9 + πk/3, где k – число целое
3)
2sin x – 3cos x = 0 ![]()
2tg x – 3 = 0
tg x = 1.5
x = arctg 1.5 + πk, где k – число целое.
a*cos x + b*sin x = c
Разделим обе части
уравнения на ![]() =
0.
=
0.
Легко проверить, что
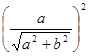 +
+ 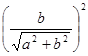 = 1
= 1
этому существует такой
угол ![]() , что
, что
cos ![]() =
=![]() , sin
, sin ![]() =
=![]()
Если c2![]() a2 + b2,
то найдётся такой угол n,что
a2 + b2,
то найдётся такой угол n,что ![]() = cos
= cos![]() . В этом случае получим уравнение cos
. В этом случае получим уравнение cos![]()
![]() cos x + sin
cos x + sin![]()
![]() sin x = cos
sin x = cos![]()
![]() cos(x –
cos(x –![]() ) = cos
) = cos![]() , равносильное данному. Решая это
уравнение, находим множество решений x =
, равносильное данному. Решая это
уравнение, находим множество решений x =![]() +
+![]() +
+ ![]() , k – число целое. Если же условие c2
, k – число целое. Если же условие c2![]() a2 + b2
не выполняется, то уравнение решений не имеет.
a2 + b2
не выполняется, то уравнение решений не имеет.
Примеры применения данного метода:
1)
sin 2x + cos 2x + 1 = 0 ![]()
![]()
![]() +
+
![]() =
=
![]()
sin
2x![]() cos
cos
![]() +
cos 2x
+
cos 2x![]() sin
sin
![]() =
=
![]()
sin(2x + ![]() ) =
) =![]()
Откуда x = (-1)k+1![]() –
– ![]() +
+ ![]() , где k – число целое.
, где k – число целое.
2) 12cos x – 5sin x + 13 = 0
Разделив обе части
уравнения на ![]() = 13,
получим
= 13,
получим
![]() cos x –
cos x – ![]() sin x = -1
sin x = -1
Полагая cos![]() =
= ![]() и sin
и sin![]() =
=![]() , записываем cos(x +
, записываем cos(x +![]() ) = -1, где
) = -1, где ![]() = arccos
= arccos![]() = arcsin
= arcsin![]() . Решая это уравнение, находим
. Решая это уравнение, находим
x + ![]() =
= ![]() +2
+2![]() k, где k – число целое
k, где k – число целое ![]() x = -
x = -![]() +
+ ![]() +2
+2![]() k, где k – число целое, откуда
k, где k – число целое, откуда
x = -arccos![]() +
+ ![]() (2k = 1), где k – число целое.
(2k = 1), где k – число целое.
Иногда
методом введения вспомогательного угла ![]() =
= ![]() решаются уравнения, содержащие одно из
выражений sin x + cos x, sin x – cos x или sin x
решаются уравнения, содержащие одно из
выражений sin x + cos x, sin x – cos x или sin x![]() cos x. При этом вводят подстановку t = sin
x + cos x или t = sin x – cos x и, учитывая, что sin 2x = 2sin x
cos x. При этом вводят подстановку t = sin
x + cos x или t = sin x – cos x и, учитывая, что sin 2x = 2sin x![]() cos x = (sin x + cos x)2
– 1 = t2 – 1 или
cos x = (sin x + cos x)2
– 1 = t2 – 1 или
sin 2x = 1 - (sin x - cos x) 2 = 1 – t2, приходят к уравнению относительно переменной t.
Примеры применения данного метода:
1) sin x + cos x = 1 – sin 2x
Обозначим t = sin x + cos
x, тогда sin 2x = t2 – 1, поэтому t = 1 – (t2 – 1) ![]() t2 + +t – 2
= 0, t1 = 1,t2 = -2, откуда:
t2 + +t – 2
= 0, t1 = 1,t2 = -2, откуда:
1) sin x + cos x = 1, x1
= (-1)k![]() –
– ![]() +
+ ![]() k, где k – число целое
k, где k – число целое
2) уравнение sin x + cos x = -2 решений не имеет, так как
![]() =
= ![]() cos
cos ![]()
![]()
![]()
![]()
![]() < 2
< 2
Заметим, что при решении
тригонометрических уравнений часто произведения разноимённых или одноимённых
тригонометрических функций вида sin![]() x* cos
x* cos![]() x, sin
x, sin![]() x*sin
x*sin![]() x, cos
x, cos![]() x*cos
x*cos![]() x следует записать в виде суммы или
разности этих функций.
x следует записать в виде суммы или
разности этих функций.
Проводят аналогии с решением подобных уравнений с прямыми тригонометрическими функциями на основе определения зависимости между этими функциями.
Примеры применения данного метода:
1) arcsin x = - ![]()
Так как – ![]() < -
< - ![]() <
< ![]() , то x = sin (-
, то x = sin (-![]() ) =
) = ![]()
2) arcsin2 x – π/2 arcsin x + π2/18 = 0
Воспользуемся методом замены: t = arcsin x, тогда
t2 – π/2 t + π2/18 = 0
Решив это уравнение, получим:
t1 = ![]() ,
t2 =
,
t2 = ![]() .
.
Т.е. arcsin x = ![]() или arcsin x =
или arcsin x = ![]() .
.
Отсюда x1 = ![]() , x2 =
, x2 = ![]() .
.
Многие тригонометрические уравнения можно решить с
помощью формул универсальной тригонометрической подстановки:
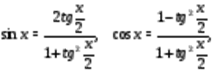
Следует отметить, что
применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку
![]() не определен в
точках х=π+2πк, поэтому в таких случаях нужно проверять,
являются ли углы х=π+2πк, корнями исходного уравнения.
не определен в
точках х=π+2πк, поэтому в таких случаях нужно проверять,
являются ли углы х=π+2πк, корнями исходного уравнения.
Пример. Решим уравнение sin x+ cos x=1
Решение:
Обращение к функции ![]() предполагает, что
предполагает, что ![]() ,
то есть х=π+2πn ,
,
то есть х=π+2πn ,![]() .
.
По формулам универсальной тригонометрической подстановки исходное уравнение примет вид:
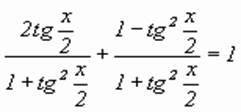 ;
;
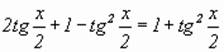 ;
;
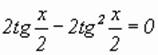 |:2
|:2
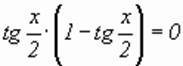 ;
;
|
|
|
|
|
|
|
|
Ответ: ![]() ,
,![]() ;
; 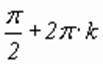 ,
, ![]()
Пример. Решите уравнение
cos2π x=x2−8x+17
Решение: cos2πx=x2−8x+17
cos2πx= (x−4)2+1 .
Оценим левую и правую части уравнения:
−1 ≤cos2πx≤ 1 и (x−4)2+1≥1 . Следовательно, равенство достигается, если cos2πx=1 и (x−4)2+1 =1.
Решая второе уравнение системы, получаем x = 4. Подставляем это значение в первое уравнение и убеждаемся в верности равенства. Следовательно, x = 4 корень исходного уравнения.
Ответ: x = 4
Решение нестандартных тригонометрических уравнений
Пример 1. Решим уравнение ![]()
Решение. Преобразуем выражение ![]() :
:
![]() .
.
Уравнение запишется в виде:
![]()
Принимая ![]() ,
получаем
,
получаем ![]() .
. ![]() ,
, ![]() .
Следовательно
.
Следовательно
Ответ. ![]() .
.
Пример 2. Решим
уравнение: ![]()
Решение. Уравнение равносильно смешанной системе:
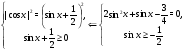
![]()
Но ![]() -
не годится.
-
не годится.
Ответ. ![]() .
.
Раскрывая знак модуля получаем более громоздкое решение. А ответ в этом случае принимает вид:
Ответ. ![]() .
.
1) В зависимости от
значений параметра a решить уравнение ![]() и определить число его корней на отрезке
и определить число его корней на отрезке ![]()
Допустимые значения
переменной х задаются системой 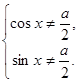
Исходное уравнение
равносильно уравнению ![]() которое равносильно совокупности двух
уравнений
которое равносильно совокупности двух
уравнений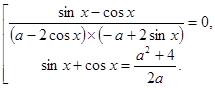
Так как ![]() то второе уравнение системы
решений не имеет. Рассмотрим первое уравнение системы. Так как здесь числитель
должен равняться нулю, т.е.
то второе уравнение системы
решений не имеет. Рассмотрим первое уравнение системы. Так как здесь числитель
должен равняться нулю, т.е. ![]() то
то ![]() При таких значениях х с учётом области
допустимых значений находим, что
При таких значениях х с учётом области
допустимых значений находим, что ![]() . Итак, при
. Итак, при ![]() из неравенств
из неравенств ![]() следует, что
следует, что ![]() Этим неравенствам удовлетворяют девять
целых значений k и, следовательно, исходное уравнение имеет девять решений на
заданном промежутке.
Этим неравенствам удовлетворяют девять
целых значений k и, следовательно, исходное уравнение имеет девять решений на
заданном промежутке.
Пусть![]() тогда первое уравнение системы
запишется в виде
тогда первое уравнение системы
запишется в виде ![]() Исключая
из множества
Исключая
из множества ![]() решения
уравнений
решения
уравнений ![]() и
и ![]() получим
получим ![]() А тогда решая неравенство
А тогда решая неравенство ![]() находим, что
находим, что ![]() и, таким образом,
существует пять целых решений рассматриваемого неравенства. Рассмотрим случай
и, таким образом,
существует пять целых решений рассматриваемого неравенства. Рассмотрим случай ![]() При таком значении
параметра а имеем уравнение
При таком значении
параметра а имеем уравнение ![]() Здесь уже надо из множества решений
Здесь уже надо из множества решений ![]() исключить решения
уравнений
исключить решения
уравнений![]() и
и ![]() Сделав это, получим
Сделав это, получим ![]() решая же неравенство
решая же неравенство ![]() окончательно находим,
что при
окончательно находим,
что при ![]() исходное
неравенство имеет четыре решения.
исходное
неравенство имеет четыре решения.
Ответ: если ![]() , то девять корней
, то девять корней ![]() если
если ![]() то пять корней
то пять корней ![]() если
если ![]() то четыре корня
то четыре корня ![]()
2) При каких значениях
параметров a и b уравнение ![]() имеет единственное решение?
имеет единственное решение?
решение задачи
основывается на том факте, что если функция f задана равенством ![]() то условия А=В, С=0
являются необходимыми и достаточными условиями того, чтобы уравнение
то условия А=В, С=0
являются необходимыми и достаточными условиями того, чтобы уравнение ![]() имело единственное
решение. Таким образом, решение задачи сводится к решению относительно
параметров a и b системы
имело единственное
решение. Таким образом, решение задачи сводится к решению относительно
параметров a и b системы 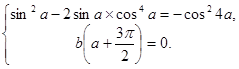
Из первого уравнения этой
системы находим, что ![]() А так как
А так как ![]() то приходим к рассмотрению систем
то приходим к рассмотрению систем 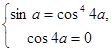 и
и 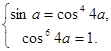
Как легко видеть,
решениями второй системы являются все значения параметра а, определяемые
равенством ![]() что
же касается первой системы, то она оказывается несовместной. Отсюда, с учётом
второго уравнения системы поиск требуемых параметров a и b сводится к поиску
решений системы
что
же касается первой системы, то она оказывается несовместной. Отсюда, с учётом
второго уравнения системы поиск требуемых параметров a и b сводится к поиску
решений системы 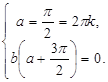 ответ
здесь очевиден.
ответ
здесь очевиден.
Ответ: ![]() любое.
любое.
3) В зависимости от
значений параметров a и b решить уравнение ![]()
Обозначив ![]() получим систему
получим систему ![]() откуда находим
откуда находим ![]() Но так как
Но так как ![]() то
то ![]() и значит
и значит ![]()
Ответ: если ![]() то
то ![]() при других значениях a и b
решений нет.
при других значениях a и b
решений нет.
4) В зависимости от
значений параметра а решить уравнение ![]()
Допустимыми значениями
переменной х являются все ![]() При таких значениях х полагая
При таких значениях х полагая ![]() перепишем уравнение в
виде
перепишем уравнение в
виде ![]() Если
Если ![]() то
то ![]() При
При ![]() записанное уравнение равносильно
совокупности
записанное уравнение равносильно
совокупности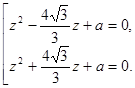 Дискриминанты обоих уравнений совокупности совпадают и имеют вид:
Дискриминанты обоих уравнений совокупности совпадают и имеют вид: ![]() Поэтому, если
Поэтому, если ![]() то решений у уравнения
нет.
то решений у уравнения
нет.
Пусть ![]() В этом случае решая уравнения
совокупности, находим, что
В этом случае решая уравнения
совокупности, находим, что ![]()
![]()
При ![]() имеем
имеем ![]() В остальных случаях все корни
определяются формулами.[4]
В остальных случаях все корни
определяются формулами.[4]
Ответ: если ![]() то решений нет; если
то решений нет; если ![]() то
то ![]() если
если ![]() , то
, то ![]() при остальных значениях параметра а
при остальных значениях параметра а ![]()
Обучение решению тригонометрических уравнений предполагает знакомство с приемами отбора корней из множеств значений неизвестного. Отбор корней в тригонометрическом уравнении может осуществляться способами: геометрическим, арифметическим и алгебраическим и функционально-графическим.
Геометрический способ
основан на использовании двух моделей: тригонометрической окружности и
числовой прямой. Тригонометрическая окружность удобна в случае, когда речь идет
об отборе корней на промежутке, длина которого не превосходит 2![]() , или если требуется
найти наибольший отрицательный или наименьший положительный корень уравнения. В
остальных случаях предпочтительнее модель числовой прямой.
, или если требуется
найти наибольший отрицательный или наименьший положительный корень уравнения. В
остальных случаях предпочтительнее модель числовой прямой.
Тригонометрическую
окружность удобно использовать при отборе корней на промежутке длина которого
не превосходит ![]() , или в случае, когда
значение обратных тригонометрических функций, входящих в серию решений, не
являются табличными.
, или в случае, когда
значение обратных тригонометрических функций, входящих в серию решений, не
являются табличными.
Арифметический способ отбора корней состоит в вычислении неизвестного при переборе значений параметров из найденных серий решений с последующей их проверкой по дополнительным условиям.
Алгебраический способ предполагает составление соответствующих дополнительным условиям неравенств и их решение относительно параметра.
Алгебраический способ наиболее эффективен когда промежуток для отбора корней достаточно большой и применение арифметического способа приводит к сложным и объемным вычислениям, а геометрический- к громоздким построениям.
Функционально-графический способ, состоит в том, что при решении тригонометрических уравнений используют графики тригонометрических функций и отбор корней осуществляют с использованием этих графиков.
Данный способ отбора корней требует умение схематичного построения графика тригонометрической функции и применение формул корней соответствующих уравнений.
Каждый из этих способов по-своему хорош и удобен для применения в том или ином случае.
Как показывает практика и анкетирование моих одноклассников, из четырёх возможных подходов к отбору корней тригонометрического уравнения по дополнительным условиям, наиболее популярен арифметический.
Отбор корней уравнения, удовлетворяющих дополнительным условиям
(корни уравнения принадлежат промежутку)
Пример 2.
Найдите все решения уравнения sin 2x = cos x , принадлежащие промежутку
![]()
Решение.
sin 2x = cos x,
2 sin x cos x – cos x = 0,
2 cos x (2 sin x – 1) = 0,
cos
x = 0 или
sin x = ![]() .
.
1)cos
x = 0, 2) sin x = ![]() ,
,
x
= ![]() ; n
; n
![]() x =
x = ![]() или
x =
или
x = ![]() , n
, n![]()
Отбор корней выполним арифметическим способом и с помощью тригонометрической окружности.
1.Если n=0,
то x = ![]() ,
, ![]()
![]() .
.
Если n=1,
то x =![]()
![]() ,
, ![]()
![]() .
.
Если n=![]() 1, то x
=
1, то x
=![]()
![]() ,
, ![]()
![]()
![]() .
.
Если n=![]() 2, то x
=
2, то x
= ![]()
![]() .
.
2.Если n=0,
то x = ![]() ,
, ![]()
![]()
![]() или x
=
или x
= ![]() ,
, ![]()
![]()
![]() .
.
Если n=1,
то для первой серии решений x
= ![]() ,
, ![]()
![]()
![]() .
.
Если n=![]() 1, то x
=
1, то x
= ![]()
![]() ,
, ![]()
![]()
или x
= ![]() ,
, ![]()
![]()
![]() .
.
Ответ:
![]() ,
, ![]() ,
, ![]() .
.
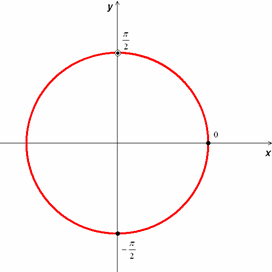
Ответ:
![]() ,
, ![]() ,
, ![]() .
.
Отбор корней арифметическим способом приводит к громоздким вычислениям. С помощью тригонометрической окружности проще и нагляднее получить корни, принадлежащие данному промежутку.
Пример 3.
Найдите все решения
уравнения ![]() , принадлежащие отрезку
[1;2] .
, принадлежащие отрезку
[1;2] .
Решение.
Воспользуемся формулами понижения степени и преобразования суммы функций в произведение:
![]()
![]() +
+![]() = 1,
= 1,
cos 4x + cos 6x = 0,
2cos 5x cos x=0,
![]() , или
, или ![]() ,
,
![]() ,
, ![]() k
k ![]()
Вторая серия решений входит в первую серию решений. (Пример 1).
Отбор корней выполним алгебраическим способом.
Решим двойное неравенство:
1![]()
10![]() ,
,
10![]() ,
,
![]() ,
,
то k=2.
Тогда x
= ![]() .
.
Ответ:![]() .
.
Отбор корней уравнения, удовлетворяющих дополнительным условиям
(корни уравнения удовлетворяют неравенству)
Пример 5.
Найдите все корни
уравнения: ![]() удовлетворяющие
неравенству cos x
удовлетворяющие
неравенству cos x ![]() 0 .
0 .
Решение.
![]() ,
, ![]() ,
,
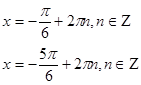
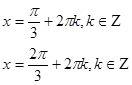
Отбор корней. Изобразим
полученные решения на тригонометрической окружности. Каждому уравнению
соответствуют две точки на тригонометрической окружности. В ответ запишем
только решения, расположенные на дуге окружности, соответствующей неравенству
cos x ![]() 0 , т.е. лежащие в I и
IV четвертях.
0 , т.е. лежащие в I и
IV четвертях.
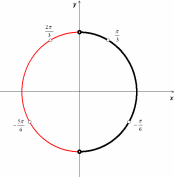 Ответ:
Ответ:
![]()
![]() , n,k
, n,k
![]()
Уравнения, в которых необходимо выполнить отбор корней в соответствии с областью допустимых значений уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. В этих заданиях нет требования - осуществить отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение отбора корней в соответствии с областью допустимых значений уравнения.
Пример 6.
Решить
уравнение: ![]()
Решение.
![]() О.Д.З sin x
О.Д.З sin x
![]() , значит
, значит ![]()
![]() ,
,
cos
x = ![]()
![]()
![]()
cos
x = 1 ![]() 1 +
1 + ![]() ,
,
![]() cos x = 0,
cos x = 0,
cos x ( cos x – 1) = 0,
cos x = 0, cos x = 1,
![]() ,
, ![]() , n,
k
, n,
k ![]()
Отбор корней.
Для отбора корней используем тригонометрическую окружность.
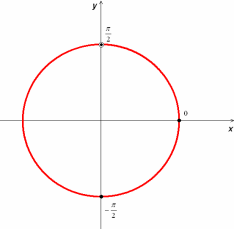
Ответ:![]() ; 2
; 2![]() ;
n,k
;
n,k
![]()
Пример 8. Решить
уравнение 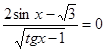
Решение.
О.Д.З. tgx > 1
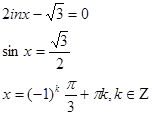 .
.
Отбор корней. Функционально-графический способ.
На промежутке ![]() , длина которого
2π, неравенству tgx>1
удовлетворяет одно число
, длина которого
2π, неравенству tgx>1
удовлетворяет одно число ![]() . Следовательно, удовлетворяют данному
уравнению все числа вида
. Следовательно, удовлетворяют данному
уравнению все числа вида ![]() +2πn,
n
+2πn,
n![]()
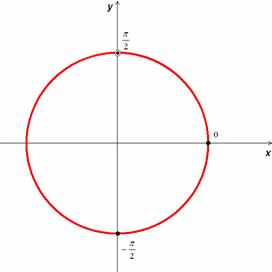
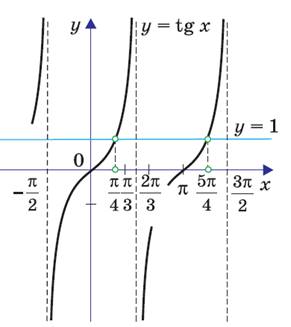
Ответ: ![]() +2πn,
n
+2πn,
n![]()
Уравнения, в которых необходимо выполнить отбор корней в соответствии с областью допустимых значений уравнения и дополнительным условием
Пример 10.
Укажите количество корней
уравнения ctg3x ![]() sin 6x - cos6x - cos12x =
0
sin 6x - cos6x - cos12x =
0
на промежутке [0;2![]() ].
].
Решение.
ctg3x
![]() sin 6x - cos6x -
cos12x = 0. О.Д.З.
sin 6x - cos6x -
cos12x = 0. О.Д.З. ![]() ,
, ![]() .
.
cos
3x ![]() sin 6x – sin 3x
sin 6x – sin 3x![]() cos 6x – sin 3x
cos 6x – sin 3x ![]() cos
12x = 0
cos
12x = 0
sin
(6x – 3x) - sin 3x ![]() cos12x = 0,
cos12x = 0,
sin
3x - sin 3x ![]() cos12x = 0,
cos12x = 0,
sin 3x(1 – cos 12x)=0,
![]() , или
1 – cos 12x
= 0,
, или
1 – cos 12x
= 0,
![]() , т.к. x
, т.к. x
![]() О.Д.З
О.Д.З ![]() ,
,
12x
= 2![]() n,
n,
![]() ,
n,k
,
n,k
![]()
Отбор корней.
Проведем отбор корней, используя тригонометрическую окружность. Для этого полученные значения в серии решений и серии ограничений изобразим на тригонометрической окружности и в ответ запишем количество не совпавших в обеих сериях значений переменной х.
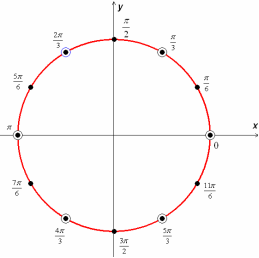 Ответ:
6.
Ответ:
6.
Пример11. Дано уравнение tg2x + tgx + 6= 0.
а) Решите уравнение.
б) Укажите корни,
принадлежащие отрезку [-2π;
- ![]() ].
].
Решение.
О.Д.З.: ![]()
![]() Тогда уравнение принимает
вид:
Тогда уравнение принимает
вид:
![]() t2
+ 5t + 6
=0 t
= -3 или t
= -2
t2
+ 5t + 6
=0 t
= -3 или t
= -2
tgx = -3 или tgx = -2
x = - arctg3 +πk, k ![]() x = - arctg2 +πn, n
x = - arctg2 +πn, n![]()
Отбор корней. Осуществляем отбор решений с использованием единичной окружности.
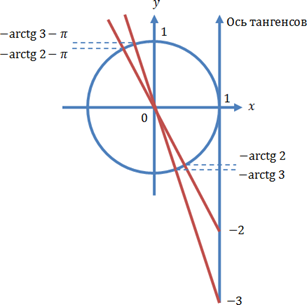
Из рисунка видно, что в
интересующий нас промежуток входят только два значения из этих серий: ![]()
Ответ: ![]()
Системы тригонометрических уравнений
Пример 12.
Решите систему уравнений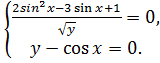
Решение.
1) Решим первое уравнение системы.
![]() О.Д.З
y >0
О.Д.З
y >0
![]() = 0
= 0
sin x = t , где −1 ≤ t ≤ 1.
2![]() − 3t +1
= 0,
− 3t +1
= 0,
t1
=1, t2 =![]() ,
,
sin
x =1, sin x =![]() ,
,
x
= ![]() + 2πn,n
+ 2πn,n ![]()
![]() ;
; ![]()
2) Решим второе уравнение системы.
![]()
![]()
Так как y >0,
то cos x![]() .
.
3) Проведем отбор корней
1 уравнения для условия cos
x![]() .
.
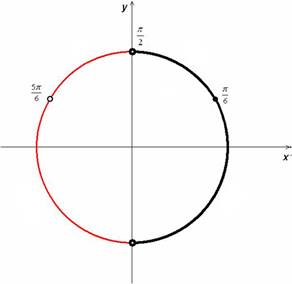
Отсюда, x = ![]() + 2πn, n ∈ Z
+ 2πn, n ∈ Z
Вернемся к системе
![]()
![]()
y = cosx
cos
![]() = cos
= cos ![]()
Таким образом, исходная
система имеет решения x = ![]() + 2πn, n ∈ Z,
y =
+ 2πn, n ∈ Z,
y = ![]() .
.
Ответ:
x =
![]() + 2πn, n ∈ Z,
y =
+ 2πn, n ∈ Z,
y = ![]() .
.
Сама задача решения уравнений порой бывает менее важна, чем нахождение частных решений, удовлетворяющих некоторому условию (принадлежащие заданному отрезку). В таких задачах после нахождения множества решений необходимо производить отбор корней. Рассмотрим пример решения таких задач.[5]
1. Уравнения, сводящиеся к квадратному.
Решить уравнение: ![]()
Решение:
Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в
виде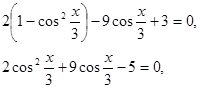
Заменой cos![]() =t
уравнение сводится к квадратному: 2t2+
9 t -5 =0, которое имеет корни t
1=
½ и t2
= -5. Возвращаясь к переменной х, получим
=t
уравнение сводится к квадратному: 2t2+
9 t -5 =0, которое имеет корни t
1=
½ и t2
= -5. Возвращаясь к переменной х, получим ![]() ,
,![]()
Второе уравнение корней не имеет, так как |cosx|≥1,
а из первого x=±![]() +6
+6![]() k,k
k,k![]() Z
Z
Ответ: =±![]() +6
+6![]() k,k
k,k![]() Z
Z
Вывод:
вводя новую переменную, нужно учитывать, что значения sin
x и cos
x ограничены отрезком ![]() , а иначе
появятся посторонние
корни.
, а иначе
появятся посторонние
корни.
2. Уравнения, решаемые разложением на множители. Задание С1 ( 2011 г.) [6]
а) Решить уравнение ![]()
б) Указать корни
уравнения, принадлежащие отрезку ![]()
Решение: а) решаем разложением левой части на множители:
группируем и выносим общий множитель за скобки, получим
![]()
Уравнение 1) решений не имеет.
Второе уравнение
однородное, решается делением почленно на cosx
≠0, получим ![]() , откуда
, откуда ![]()
б) 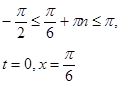
Ответ: а) ![]() б)
б)![]()
Вывод:
1.При решении уравнения такого вида, во – первых, нужно знать, что |sinх|≤1 и |cosx|≤1, и уравнение sinx=-2 решений не имеет;
2.Обосновать деление на cosx≠о (так как, если cosx=0,то sinх=0, а это невозможно);
3.Обоснованно произвести отбор корней, принадлежащих данному промежутку.
3.Уравнение на применение
формул приведения ![]() (
2010 г.)
(
2010 г.)
а) решить уравнение;
![]() б) Указать корни,
принадлежащие отрезку
б) Указать корни,
принадлежащие отрезку
Решение: Используя формулы приведения, получим:
sin 2 x – cos x =0,
2 sinx cosx- cosx =0,
сosx (2 sinx -1 )=0, откуда cosx= 0 или sinx =½,
![]()
![]()
б) Найдем значения к, при которых корни будут принадлежать
указанному промежутку. Решение представим в виде:
![]()
![]()
![]() б) Найдем значения к,
при которых корни будут принадлежать указанному промежутку.
б) Найдем значения к,
при которых корни будут принадлежать указанному промежутку.
![]()
![]() 2)
2)
![]()
Ответ: а) ![]()
![]()
б) ![]()
Вывод:
При решении уравнения
такого вида, необходимо знать формулы приведенного уравнения и правильно её
применить; уметь представлять решение![]() на две серии корней; правильно выбрать
корни, принадлежащие заданному отрезку.[7]
на две серии корней; правильно выбрать
корни, принадлежащие заданному отрезку.[7]
4. Системы тригонометрических уравнений
(2010).
Решить систему уравнений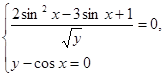
Решение: О.Д.З ![]()
Дробь равна нулю, если числитель равен 0, а знаменатель не равен 0.
Из уравнения 2sin2x – 3 sinx +1 =0, решая методом введения новой переменной, находим
![]() или
sin x=1.
или
sin x=1.
1)Пусть ![]() ,
тогда
,
тогда ![]() и
у = cos x
=
и
у = cos x
= ![]() ›0 ( используя основное
тригонометрическое тождество)
›0 ( используя основное
тригонометрическое тождество)
либо ![]() и
и ![]() - нет решения.
- нет решения.
2) Пусть sinx = 1, тогда у = cos x = 0 – нет решения.
Ответ: ![]() и
у =
и
у = ![]()
Вывод:
1) нужно учитывать ограниченность тригонометрических функций;
2) Записывать и учитывать О.Д.З.
5. Использование формул приведения.
а) Решите уравнение:
![]()
б) Найдите
все корни этого уравнения, принадлежащие промежутку ![]()
Решение.
Используя формулу приведения
![]() и
формулу синуса двойного угла
и
формулу синуса двойного угла ![]() ,
получаем:
,
получаем:
![]()
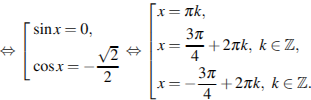
Заданный промежуток
имеет длину π, поэтому ему принадлежит не больше двух корней из первой
серии, не больше одного корня из второй серии и не больше одного корня
из третьей серии. Во второй серии решений из отрезка нет, из первой и
третьей серии это числа ![]()
Ответ: а) ![]() б)
б)
![]()
Различные примеры заданий под №13[8]
6. а) Решите уравнение cos2x − 3cosx + 2 = 0.
б) Найдите все корни
уравнения, принадлежащие отрезку ![]()
Решение.
а) Преобразуем уравнение:
![]()
![]()
Получаем ![]() или
или
![]() откуда
откуда
![]() или
или
![]()
где ![]()
б) На отрезке ![]() корни
отберём с помощью единичной окружности.
корни
отберём с помощью единичной окружности.
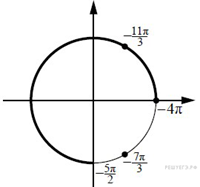
Получаем ![]() и
и
![]()
Ответ: а) ![]() б)
б)
![]()
7. а)
Решите уравнение ![]()
б) Укажите корни этого
уравнения, принадлежащие отрезку ![]()
Решение.
![]()
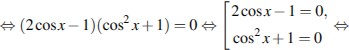
![]()
б) Укажем корни этого
уравнения, принадлежащие отрезку ![]() Покажем
на единичной окружности.
Покажем
на единичной окружности.
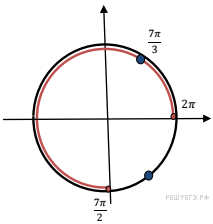
Ответ: а) ![]() б)
б)
![]()
8. а)
Решите уравнение ![]()
б) Укажите корни этого
уравнения, принадлежащие отрезку ![]()
Решение.
Сведём уравнение к квадратному,
используя формулу ![]()
Имеем:
![]()
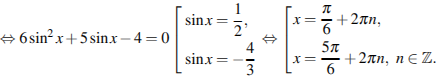
б) С
помощью числовой окружности отберём корни, принадлежащие отрезку ![]() (см.
рис.), получим число
(см.
рис.), получим число ![]()
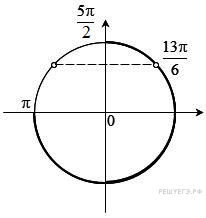
Ответ: а) ![]() б)
б)
![]()
9. а)
Решите уравнение ![]() .
.
б) Укажите его корни,
принадлежащие отрезку ![]()
Решение.
Сделаем замену ![]() ,
получим квадратное уравнение
,
получим квадратное уравнение ![]() корнями
которого являются числа
корнями
которого являются числа ![]() и
и
![]() Уравнение
Уравнение
![]() не
имеет решений, а из уравнения
не
имеет решений, а из уравнения ![]() находим
искомые корни:
находим
искомые корни:
![]() или
или
![]() ;
;
![]() .
.
Найдем корни, принадлежащие
отрезку ![]() Решим
неравенства:
Решим
неравенства:
![]()
![]() или
или
![]() ;
;
![]()
Соответствующие
найденным значениям параметров корни: ![]()
![]() и
и
![]() .
.
Ответ: а)![]() .
б) Заданному
отрезку принадлежат корни
.
б) Заданному
отрезку принадлежат корни ![]() и
и
![]() .
.
10. а)
Решите уравнение ![]()
б)
Укажите корни, принадлежащие отрезку ![]()
Решение.
Сделаем замену ![]() и
получим квадратное уравнение
и
получим квадратное уравнение ![]() откуда,
откуда,
![]() Уравнение
Уравнение
![]() не
имеет решений, а из уравнения
не
имеет решений, а из уравнения ![]() находим
находим
![]()
Найдем корни, принадлежащие
отрезку ![]()
![]()
![]()
Отрезку ![]() принадлежат
корни
принадлежат
корни ![]()
Ответ: a)
![]() б)
б)
![]()
Вывод: Ответ записать с учётом О.Д.З.
№11 Найдем все решения уравнения, принадлежащие промежутку [-π;π]
cos 2x + sin2x = cos x
решениями являются числа вида
x
= ![]() и x
= 2πn, n
и x
= 2πn, n
![]()
Отбор корней можно проводить различными способами. Например,
I способ:
k = 0 x = ![]() n = 0 x
= 0
n = 0 x
= 0 ![]()
k = 1 x = ![]() n
= ± 1 x = ± 2π
n
= ± 1 x = ± 2π ![]()
k
= -1 x = ![]() n
= ± 2 x = ±2π
n
= ± 2 x = ±2π ![]()
k
= -2 x = ![]() если
|n|
> 2, то x
если
|n|
> 2, то x ![]()
k
= 2 x = ![]()
если |k|
> 2, то x ![]()
Ответ: решениями
уравнения из промежутка [-π;π] являются х = ![]()
II способ: x
![]() , т.е.
–π ≤ х ≤ π
, т.е.
–π ≤ х ≤ π
Значит, –π ≤ ![]() ≤
π –π ≤ 2πп
≤ π
≤
π –π ≤ 2πп
≤ π
–1 ≤ ![]() ≤
1 –1 ≤ 2п ≤ 1
≤
1 –1 ≤ 2п ≤ 1
–![]() ≤ k
≤
≤ k
≤ ![]() –
–![]() ≤ n
≤
≤ n
≤ ![]()
k- целое число, значит, n – целое число, значит,
k = -1; 0 n =0
Таким образом, искомыми корнями являются числа при k
= -1 х = ![]() ,
,
при k
= 0 х = ![]() ,
,
при n = 0 х = 0.
Ответ: х = ![]()
№12. Найдем число
корней уравнения cos2
2х + cos2
6х = 1, принадлежащие отрезку ![]()
При решении этого уравнения учащиеся могут воспользоваться формулой понижения степени.
Так в данном уравнении две серии решений:
х = ![]() и х =
и х = ![]()
и после отбора корней получается, что п = 0; 1;
2; 3, k = 0; 1. Если бы буква
была одна, то можно допустить ошибку: посчитать, что различных корней
всего четыре, тогда как окончательно уравнение имеет 6 различных корней из
промежутка ![]() .
[9]
.
[9]
В проделанной мною работе были изучены различные методы решения тригонометрических уравнений, рассмотрены рекомендации по отбору корней тригонометрических уравнений.
Я рассмотрел 9 основных методов решения тригонометрических уравнений, выявил положительные и отрицательные черты этих методов, решил уравнения, которые не подлежат решению стандартными способами, выявил другие методы решения тригонометрических уравнений.
При решении тригонометрических уравнений следует умело анализировать зависимости между различными тригонометрическими функциями и уметь творчески подходить к работе.
Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений следующая: решение заданного уравнения сводится к решению элементарных уравнений. Средства решения: преобразования, разложения на множители, замена неизвестных. Ведущий принцип: не терять корней. Это означает, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей "цепочки" (или совокупность уравнений в случае ветвления) являлось следствием предыдущего. Одна из особенностей тригонометрических уравнений заключается в том, что ответ во многих случаях может быть записан различными способами.
Одним из возможных методов отбора корней является проверка. Сразу заметим, что в случае тригонометрических уравнений трудности, связанные с отбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями. Ведь проверять приходится серии, состоящие из бесконечного числа членов.
Способы отбора корней в тригонометрических уравнениях:
1. Арифметический способ: перебор значений целочисленного параметра и вычисление корней.
2. Алгебраический способ: решение неравенства относительно неизвестного целочисленного параметра и вычисление корней.
3. Геометрический способ:
- изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений;
- изображение корней на числовой прямой с последующим отбором с учетом имеющихся ограничений.
4. Функционально-графический способ:отбор корней с использованием графика простейшей тригонометрической функции.
Рекомендации при отборе корней в тригонометрических уравнениях:
Арифметический способ самый простой, но он становится не эффективным в следующих случаях:
-заданные ограничения охватывают большой промежуток, и последовательный перебор значений приводит к громоздким вычислениям;
-серии решений содержат нетабличные значения обратных тригонометрических функций;
-требуется определить количество корней уравнения, удовлетворяющих дополнительным условиям.
Тригонометрическую окружность удобно использовать при отборе корней на промежутке, длина которого не превосходит 2π, или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.
При отборе корней, если есть О. Д. З., необходимо выполнить сначала отбор по О. Д. З. а затем по условию к уравнению.
Данная работа имеет большое практическое значение, т.к. тригонометрические уравнения часто содержатся в материалах ЕГЭ и экзаменов для поступления в вузы, а в школьном курсе математике недостаточно изучаются. Исследование может быть употреблено как материал для проведения предметных факультативов по алгебре или при подготовке к ЕГЭ.
Основные формулы тригонометрии
1) основное тригонометрическое тождество sin2α +cos2 α= 1,
Деля это уравнение на квадрат косинуса и синуса соответственно имеем
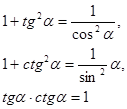
2)формулы двойного аргумента sin2α =2 sinα cos α,
cos 2α = cos2 α - sin2α,
cos 2α = 1- 2sin2α,
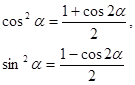
3)формулы понижения степени:
sin
2 x = ![]()
cos
2 x = ![]()
4) формулы синуса и коссинуса суммы и разности двух аргументов:
sin(α+β)=sinα cos β +cos α sin β
sin(α-β)=sinα cos β -cos α sin β
cos(α+β)=cosα cos β +sin α sin β
cos(α-β)=sinα cos β +sinα sin β
5)Формулы приведения
Формулами приведения называются формулы следующего вида:
![]()
![]()
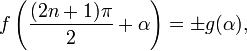
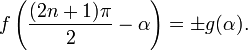
6. Формулы суммы и разности тригонометрических функций
![]()
![]()
![]()
![]()
![]()
7. Чётность
Косинус— чётная, синус, тангенс и котангенс— нечётные, то есть:
![]()
![]()
![]()
![]()
8. Непрерывность
Синус и косинус — непрерывные
функции. Тангенс и имеет точки
разрыва ![]()
![]() , котангенс 0; ±π; ±2π;…
, котангенс 0; ±π; ±2π;…
9. Периодичность
Функции y = cos x, y = sin x — периодические с периодом 2π,
функции y = tg x и y = ctg x — c периодом π.
10. Знаки тригонометрических функций по четвертям
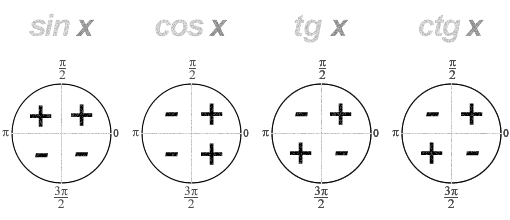
(Таблица значений тригонометрических функций некоторых углов)
|
Угол (a) |
Тригонометрическая функция |
||||||
|
Градусы |
Радианы |
sin a |
cos a |
tg a |
ctg a |
sec a |
cosec a |
|
0° |
0 |
0 |
1 |
0 |
∞ |
1 |
∞ |
|
30° |
|
|
|
|
|
|
2 |
|
45° |
|
|
|
1 |
1 |
|
|
|
60° |
|
|
|
|
|
2 |
|
|
90° |
|
1 |
0 |
∞ |
0 |
∞ |
1 |
|
120° |
|
|
|
|
|
-2 |
|
|
135° |
|
|
|
-1 |
-1 |
|
|
|
150° |
|
|
|
|
|
|
2 |
|
180° |
|
0 |
-1 |
0 |
∞ |
-1 |
∞ |
|
210° |
|
|
|
|
|
|
-2 |
|
225° |
|
|
|
1 |
1 |
|
|
|
240° |
|
|
|
|
|
-2 |
|
|
270° |
|
-1 |
0 |
∞ |
0 |
∞ |
-1 |
|
300° |
|
|
|
|
|
2 |
|
|
315° |
|
|
|
-1 |
-1 |
|
|
|
330° |
|
|
|
|
|
|
-2 |
|
360° |
|
0 |
1 |
0 |
∞ |
1 |
∞ |
1. Гилемханов Р.Г. О преподавании тригонометрии в 10 классе//Математика в школе. 2001-№ 6 -с. 26-28.
2. Глазков Ю. А. Математика. ЕГЭ: сборник заданий и методических рекомендаций/ Ю. А. Глазков, И. К. Варшавский, М. Я. Гаиашвили. – М.: Издательство «Экзамен», 2016
3. ЕГЭ. Контрольно-измерительные материалы. М: Просвещение, 2002-2017г.
4. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)
5. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва, «Просвещение», 1994.
6. Крамор В.С. Тригонометрические функции. - М.: Просвещение, 1979.
7. Математика. ЕГЭ – 2017: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2017. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России)
8. Синакевич С.В. Тригонометрические уравнения - М.: Учпедгиз, 1959.
9. Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.
10. Электронный ресурс «Математика»/ URL: http://www.webmath.ru/poleznoe/trig_formules.php
11. Электронный ресурс «Решу ЕГЭ»/ URL: http://reshuege.ru/
[1] Гилемханов Р.Г. О преподавании тригонометрии в 10 классе//Математика в школе. 2001-№ 6 -с. 26-28.
[2] Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва, «Просвещение», 1994.
[3] Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.
[4] Синакевич С.В. Тригонометрические уравнения - М.: Учпедгиз, 1959.
[5] ЕГЭ. Контрольно-измерительные материалы. М: Просвещение, 2002-2017г.
[6] Электронный ресурс «Решу ЕГЭ»/ URL: http://reshuege.ru/ [Дата обращения к ресурсу: 10.01.2018]
[7] Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России)
[8] ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)
[9] Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.