Недосказанные факты о треугольниках.

Недосказанные факты о треугольниках.

А.П. Титченко

Аннотация

Жұмысзерттеугеарналғанжәнедәлелдеуқасиеттерін, үшбұрыштың, кімніңбұрыштарықұрайдыгеометриялық прогрессию. Айту қиын, неге бұлтақырыпбұрын да қозғалды математика, бірақ факт болыпқалады, бұлжұмыстыңмазмұныарналдымүлдембелгісіз, ал сондықтан, зерттелген теоремам қасиеттерітуралыүшбұрыштыңеңісбұрыштарыорналасқангеометриялықретпен.

Жұмысзақымдайдыкеңдігіменқамтылатын материал.

Материал зерттеуболыптабылады, сондықтан да дамытуғаықпалетеді, танымдыққызығушылығын, аналитикалыққабілеттеріндамыту, әртүрліәдістерінқабылдаужәнеақпараттыөңдеу. Жұмыстақойылғанмақсаты, міндеттері, пәніжәнезерттеунысаны, өзектілігі, жаңалығы, - депатапкөрсетедізерттеужұмысыныңсипаты. Автор дәлелдейді, жәнежүйелейдіқасиеттері, үшбұрыш, еңісбұрыштарықұрайтынгеометриялықреттілігібұлреттепайдаланадығанаемес материал, оқуқұралы, бірақжәнеқосымшаматериалдытереңзерттеуүшін. Жұмыстарорындалуыжоғарыдеңгейде, құрамындабірқатаржаңа, бұрындәлелденгенфактілерді геометрия білдіретінпрактикалыққызығушылық.

Аннотация

Работа посвящена исследованию и доказательству свойств треугольника, чьи углы составляют геометрическую прогрессию. Сложно сказать, почему данная тема ранее не была затронута в математике, но остается фактом, что содержание работы посвящено совершенно неизвестным, а поэтому и не изученным теоремам о свойствах треугольника с углами, находящимися в геометрической последовательности.

Работа поражает широтой охватываемого материала.

Материал является исследовательским, поэтому способствует развитию познавательного интереса, аналитических способностей, различных способов восприятия и обработки информации. В работе поставлены цель, задачи, предмет и объект исследования, актуальность, новизна, что указывает на исследовательский характер работы.Автор доказывает и систематизирует свойства треугольника, с углами составляющими геометрическую последовательность при этом использует не только материал учебного пособия, но и дополнительный материал, предназначенный для углубленного изучения. Работа выполнена высоком уровне, содержит ряд новых, ранее не доказанных фактов в геометрии, представляющих практический интерес. 

Annotation

The paper is devoted to the study and proof of the properties of a triangle whose angles form a geometric progression. It is difficult to say why this topic was not previously touched upon in mathematics, but the fact remains that the content of the work is devoted to completely unknown, and therefore not studied, theorems about the properties of a triangle with angles in a geometric sequence.

The work impresses with the breadth of the material covered.

The material is research, so it contributes to the development of cognitive interest, analytical abilities, and various ways of perceiving and processing information. The paper sets the goal, objectives, subject and object of research, relevance, novelty, which indicates the research nature of the work. The author proves and systematizes the properties of a triangle, with the angles forming a geometric sequence, while using not only the material of the textbook, but also additional material intended for in-depth study. The work is performed at a high level, contains a number of new, previously unproven facts in geometry that are of practical interest.

ВВЕДЕНИЕ

Работа касается не то, чтобы малоисследованной, а совершенно неисследованной области: треугольников, чьи углы составляют геометрическую прогрессию. Почему такие треугольники с такими неожиданными, интересными и захватывающими свойствами, оказались в тени, пусть выясняют историки математики, а мы вернемся к работе, которая поражает широтой охватываемого материала.

Простейший из многоугольников–треугольник–играет в геометрии особую роль. Такова уже природа избранного треугольника с углами, составляющими геометрическую прогрессию, что его своеобразие и свойства хорошо высвечиваются именно н сопоставлении с другими типами треугольников и другими типами геометрических объектов. Исследуемый треугольник так богат свойствами, что их невозможно не только не исследовать, но и доказать в силу их полезности для расширения и углубления раздела геометрии «Треугольники»

Предмет исследования- свойства треугольников с угламии.

Цель работы: найти, исследовать и доказать свойства треугольника, углы которых составляют геометрическую прогрессию.

Если о треугольниках, стороны которых составляют арифметическую прогрессию еще можно отыскать информацию, то о треугольниках, углы которых составляли бы геометрическую прогрессию, систематических исследований не проводилось. Между тем, свойства такого рода треугольников богаты, глубоки и интересны.

Гипотеза: существует треугольник, углы которого составляют геометрическую прогрессию обладающей отличительными, неизученными свойствами.

Значимость работы может быть рассмотрена в двух аспектах: а) научном, б) практическом.

Так как в работе доказаны свойства нового объекта, а именно треугольника, углы которого составляют геометрическую прогрессию, то работа имеет научное значение.

Работа относится к внутренним областям математики и прямого выхода в практику не имеет, а выходит в нее опосредствованно, через другие разделы математики. ванным в расширении и углублении знаний в области геометрии. Материал работы может быть использован в математических классах, кружках и факультативах в качестве пособия для ознакомления с особыми типами треугольников и их свойствами. Окажется он полезным и для самих учителей.

Треугольники, углы которых составляют геометрическую прогрессию

Треугольники, углы которых составляют геометрическую прогрессию это треугольники с углами и.Эти треугольники отличаются большим набором интересных свойств, нахождением и доказательством которых мы будем заниматься в нашем проекте.

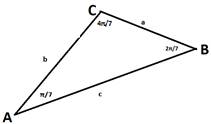
Доказательство: Пусть имеется треугольник АВС с указанными свойствами:         ∠A = , ∠B = ,   ∠C =  и сторонами, равными а. b. с. (рис. 1).Тогда используя расширенную теорему синусов для произвольного треугольника ,где a {\displaystyle a},b {\displaystyle b},c {\displaystyle c} — стороны треугольника, ∠A,B,C{\displaystyle \alpha ,\beta ,\gamma } — соответственно противолежащие им углы, а {\displaystyle R}R — радиус окружности, описанной около треугольника:  и . Отсюда получим:          и используя формулу двойного угла синуса

sin(2α) = 2sin(α)cos(α) получаем =  .Тогда длина стороны а может быть выражена следующим равенством: a= ,из которого выразим в : в = 2а * cos.

Аналогично выразим длину стороны с через в:  ;  =    ; b=  из которого окончательно выразим длину с через b: c = 2b * cos.

Для рассмотрения выражения длины стороны а через с нам понадобится формула приведения тригонометрии:sin= sin(π-)= sin () и получаем 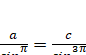. Аналогично

sinsin ( π-)=sin=2 sincos., тогда  = 

Получаем, что длина стороны а может быть выражена следующим равенством a= из которого выразим с : с = 2а * cos.

Сложим теперь все три равенства, предварительно возведя каждое в квадрат, получим

a²+ b²+c²=4a²+4b²+4c².С другой стороны:a²=4R², b²=4R²,c²=4R². Откуда окончательно

a²+b²+c²=4a²+4b²+4c²=4=4R²(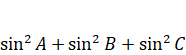)=4R²(2+2cosA•cosB•cosC)=4R²• =7R².

Что и требовалось доказать.

Теорема 2: Если a, b, c стороны треугольника АВС с угламии, то сторона а равна половине среднего гармонического двух других его сторон. 

Используя это утверждение можно показать, что b=, c=

Теорема 3: Еслиh_a, h_b, h_c   - высоты, опущенные соответственно на стороны а,b,c треугольника АВС с углами   ∠A= ∠B= ,      ∠C= , то h_a=h_b + h_c

Теорема 4:Суммы квадратов высот треугольника АВС с угламииравны половине суммы квадратов его сторон:h_a²+ h_b²+ h_c²=

Скачано с www.znanio.ru