Лабораторная работа №2

Тема: Np-полные задачи. Изоморфизм графов

Цель: Закрепление знаний о Np-полных задачах, формирование навыков определения изоморфности графов.

Вид работы: индивидуальный.

Время выполнения: 6 часов.

Теоретический материал

Понятие NP – полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (журнал «Проблемы передачи информации», 1973,т.9, вып. 3) и основывается на понятии сводимости одной задачи к другой.

Сводимость может быть представлена следующим образом: если мы имеем задачу 1 и решающий эту задачу алгоритм, выдающий правильный ответ для всех конкретных проблем, составляющих задачу, а для задачи 2 алгоритм решения неизвестен, то если мы можем переформулировать (свести) задачу 2 в терминах задачи 1, то мы решаем задачу 2.

Таким образом, если задача 1 задана множеством конкретных проблем D_A1, а задача 2 – множеством, и существует функция f_s (алгоритм), сводящая конкретную постановку задачи 2 (d_А2) к конкретной постановке задачи 1(d_А1): f_s(d₍₂₎ÎD_A2) = d₍₁₎ÎD_A1, то задача 2 сводима к задаче 1.

Если при этом F_A (f_s) = O(n^k), т.е. алгоритм сведения принадлежит классу P, то говорят, что задача 1 полиномиально сводится к задаче 2.

Принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 – языком L2, то полиномиальная сводимость обозначается следующим образом: L2 £ _p L1.

Определение класса NPC (NP-complete) или класса NP-полных задач требует выполнения следующих двух условий: во-первых, задача должна принадлежать классу NP (L Î NP), и, во-вторых, к ней полиномиально должны сводиться все задачи из класса NP (L_x £ _P L, для каждого L_x Î NP. Для класса NPC доказана следующая теорема: Если существует задача, принадлежащая классу NPC, для которой существует полиномиальный алгоритм решения (F = O(n^k)), то класс P совпадает с классом NP, т.е. P=NP .

Схема доказательства состоит в сведении любой задачи из NP к данной задаче из класса NPC с полиномиальной трудоемкостью и решении этой задачи за полиномиальное время (по условию теоремы).

В настоящее время доказано существование сотен NP– полных задач, но ни для одной из них пока не удалось найти полиномиального алгоритма решения. В настоящее время исследователи предполагают следующее соотношение классов  – P ¹ NP, то есть NP \ P ¹ , и задачи из класса NPC не могут быть решены (сегодня) с полиномиальной трудоемкостью.

Рассмотрим схему из функциональных элементов «и», «или», «не» с n битовыми входами и одним выходом, состоящую не более, чем из O(n^k) элементов – рис 6.4

Будем понимать под выполняющим набором значений из множества {0,1} на входе схемы, такой набор входов – значения x₁,…,x_n, при котором на выходе схемы будет значение «1».

Формулировка задачи – существует ли для данной схемы выполняющий набор значений входа. Очевидно, что задача принадлежит классу NP – проверка предъявленного выполняющего набора не сложнее количества функциональных элементов, и следовательно не больше чем O(n^k).

Это была одна из первых задач, для которой была доказана ее NP полнота, т.е. любая задача из класса NP полиномиально сводима к задаче о выполнимости схемы.

Решение этой задачи может быть получено перебором всех 2ⁿ возможных значений входа с последующей проверкой на соответствие условию выполняющего набора. В худшем случае придется проверить все возможные значения входа, что приводит к оценке F^{^}(n) = O(n^k * 2ⁿ). Для этой, как и для всех других NP–полных задач не известен полиномиальный алгоритм решения.

Задача о сумме

Уже рассмотренная задача о сумме также является NP–полной, отметим, что если количество слагаемых фиксировано, то сложность задачи является полиномиальной, так как:

-       для 2-х слагаемых Þ С_N²=(N*(N-1))/(1*2) = O(N²);

-       для 3-х слагаемых Þ C_N³=(N*(N-1)*(N-2))/(1*2*3) = O(N³).

Однако в общем случае придется перебирать 2^N различных вариантов, так как по биномиальной теореме (a+b)^N = å c_N^k * a^N-k * b^k, а при a=b=1, имеем: (1+1)^N = å C_N^k = 2^N, следовательно, F_A (N, V) = O(N * 2^N).

Задача о клике

Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G.

Задача состоит в определении клики в заданном графе G

Поскольку в полном графе на m вершинах имеется m(m-1)/2 ребер, то проверка, является ли данный граф полным, имеет сложность O(m²). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует C_n^m различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:

F(m, n) = O(m² * C_n^m) = O(m² * n^m).

Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае:

Задача изоморфизма подграфу

Даны два графа, G1 и G2. Множество вершин первого графа обозначим V1, а второго — V2 . Пусть |V1| > | V2| = п. Требуется ответить на вопрос: найдется ли в графе G1 подграф H, изоморфный графу G2?

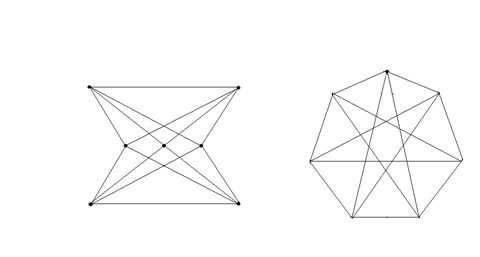
Два графа G1 и G2 называются изоморфными, если между их вершинами установлено взаимнооднозначное соответствие, такое, что любые две вершины графа G1 соединены так же, как и соответствующие вершины графа G2. Рассмотрим графы 1 и 2 на рис. 1.

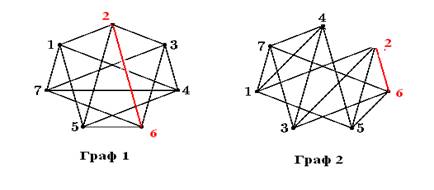
Рисунок 1 – Изоморфные графы

Для того чтобы выяснить, изоморфны ли два графа имеющие  вершин, в общем случае требуется выполнить  попарных сравнений, а для распознавания изоморфного вложения графа , имеющего  вершин, в граф , у которого  вершин, необходимо провести  сравнений. Поэтому даже при относительно небольшом количестве элементов в графах (порядка 100) решение задачи об изоморфизме методом полного перебора практически не реально, необходимо использовать для этой цели специальные методы.

Ход работы:

1. Согласно своему варианту определить являются ли графы изоморфными. Решить задание  без использования  ЭВМ;

2. Написать и отладить программу в соответствии с заданием.

Задания:

Вариант 1

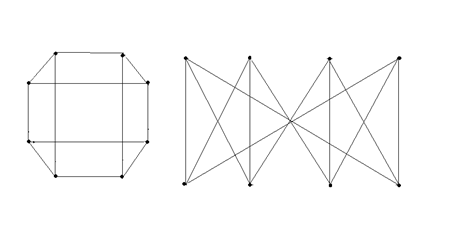
Вариант 2

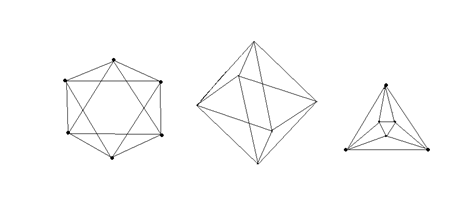
Вариант 3

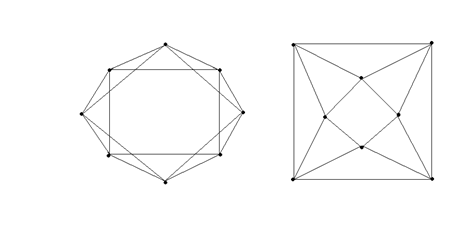
Вариант 4

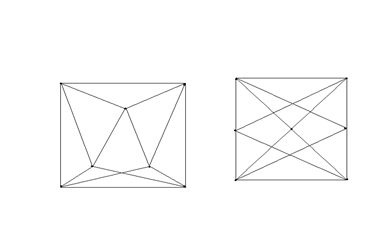
Вариант 5

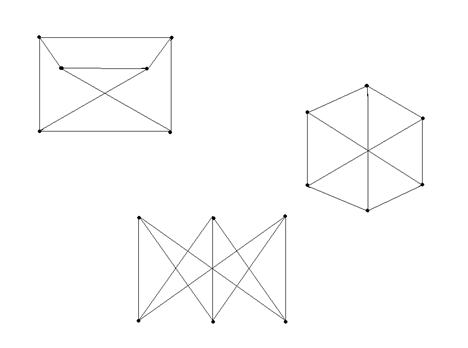
Вариант 6

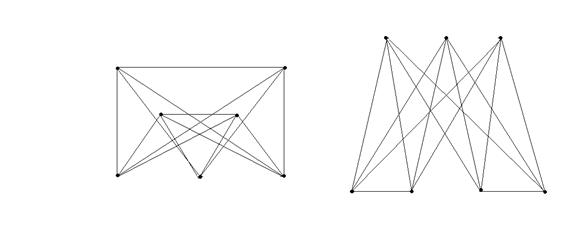         Вариант  7

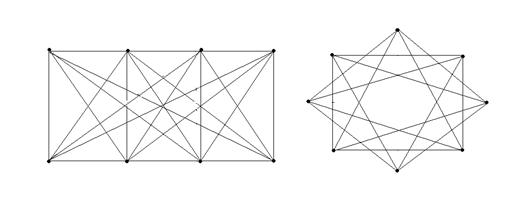
Вариант 8

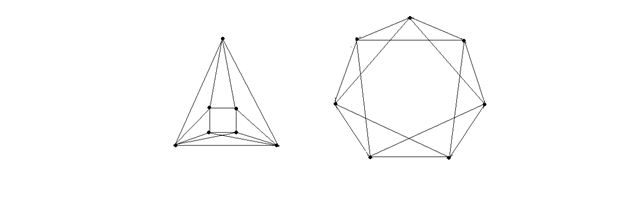
Вариант 9

Контрольные вопросы:

1)  Дайте определение Np-полной задачи.

2)  Какие задачи относятся к NP-полным задачам?

3)  Приведите примеры Np-полных задач.

Скачано с www.znanio.ru