О ЧИСЛЕ РАЗЛИЧНЫХ ФОРМ МНОГОУГОЛЬНИКОВ

О ЧИСЛЕ РАЗЛИЧНЫХ ФОРМ МНОГОУГОЛЬНИКОВ

Многоугольником мы будем называть, как это принято в элементарной геометрии, замкнутую ломаную линию, расположенную иа плоскости без самопересечений. Известно, что многоугольник делит плоскость на две части, из которых одна лежит целиком в конечной части плоскости, а другая содер­жит сколько угодно далекие точки плоскости.

О       первой части говорят, что она лежит внутри многоугольника; о второй,— что она лежит вне многоугольника. Над многоуголь­ником мы будем производить операцию, кото­рую назовем деформацией многоугольника. Эта операция состоит в том, что все вер­шины многоугольника заставляют непрерывно скользить по некоторым кривым в плоскости многоугольника, причем все его стороны соответствующим образом укорачиваются или удлиняются.

Так, например, четырехугольник ABCD путем деформации можно превратить в четырехугольник ABCD' (черт. 1); для этого достаточно заставить вершину D пробежать отрезок DDСторона AD при этом укорачивается и превращается в отрезок AD¹, сторона CD удлиняется и превращается в от­резок CL>'. Toiho также че.ырехугольник ABCD можно путем деформации превратить в четырехугольник- ABCD* (черт. 2); для этого достаточно заставить вершину D про­бежать отрезок DD".

Единственное ограничение, которое мы введем, состоит в том, что в процессе деформации не должно происходить само­пересечений многоугольника. Очевидно, даже при наличии этого ограничения любой много­угольник может быть преобразован путем деформации во всякий другой многоуголь­ник с тем же числом вершин.

При преобразовании одного многоуголь­ника в другой с помощью деформации могут представиться два различных случая: либо преобразование одного многоугольника в дру­гой можно выполнить таким образом, что во время деформации число сторон многоуголь­ника не изменяется, либо при преобразовании одного многоугольника в другой число сто­рон многоугольника хотя бы один раз умень­шается, независимо от того, какой именно деформацией выполняется преобразование. Мы будем говорить, что многоугольники имеют одну и ту же форму, если налицо первый случай; во втором случае мы будем говорить, что многоугольники имеют различную форму. Т.к. в предыдущих примерах четырехугольники ADCD и ABCD' имеют одну и ту же форму, в то время как четырех­угольники BCD и ABCD" имеют различную форму.

Действительно, при деформации че­тырехугольника ABСD в четырехугольник АВСD", в тот момент, когда вершина D попадает в точку Е, четырехугольник ABCD превращается в треугольник ABC. При этом невозможно провести это преобразование так, чтобы в процессе деформации четырехуголь­ник ABCD не превращался в треугольник.

Наша задача будет состоять в определе­нии числа различных форм n-угольников для любого значения п. Это число будем обоз­начать символом Ф_n.

Для малых значений п числа Ф_n легко определяются путем непосредственного вычер­чивания многоугольников. С возрастанием п число Ф_я очень быстро возрастает, и опре­деление его делается весьма затруднительным.  Приводим значения Ф_я для небольших зна­чений n:

Ф₃ — 1; Ф₄ = 2;Ф₅ = 4; Ф₆ = 8; Ф₇ = 15.

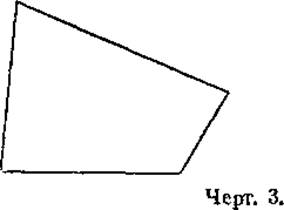
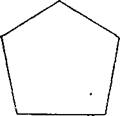
На чертежах 3 и 4 изображены различные формы четырех- и пятиугольников.

Две стороны многоугольника, имеющие общую вершину, образуют на плоскости два угла, из которых один больше 180°, а другой — меньше 180°. Один из этих углов принадлежит той части плоскости, которая лежит внутри многоугольника; этот угол будем называть внутренним углом многоугольника. Если внутренний угол многоуголь­ника больше 180°, мы будем называть его входящим углом. Так, на чертеже 2 четырех­угольник ABCD" имеет входящий угол AD"C. Внимательный читатель сейчас же заметит, что два одноименных многоугольника имеют одну и ту же форму, если они имеют одно и то же число входящих углов, которые на контур IX многоугольников одинаковым об­разом чередуются с остальными их углами.

Если же два одноименных многоугольника имеют разное число входящих углов или же равное число входящих углов чередуется с другими углами на контурах этих двух много­угольников различным образом, то эти много­угольники и дают разную форму.

Действительно, в этом случае при дефор­мации по крайней мере один угол, который до того не был входящим, делается входящим, или наоборот. Но при деформации много­угольника его углы изменяются непрерывно, поэтому, изменяясь от значения, меньшего 180°, до значения большего 180°, или при обратном изменении, этот угол должен по крайней мере один раз принимать значение, равное 180°. Но в тот момент, когда этот угол равен 180°, число сторон многоугольника уменьшается. Из изложенного видно, что это уменьшение числа сторон происходит неза­висимо от того, как производилась дефор­мация, а лишь от того, что входящие углы на контурах этих двух многоугольников расположены различным образом. Отсюда следует, что рассматриваемые многоугольники имеют различную форму.

Заметим, что какова бы ни была форма многоугольника, но по крайней мере три его угла не являются входящими.

Из изложенного читатель может видеть, что рассмотренная нами задача в ее общей постановке чрезвычайно сложна и интересна.

Скачано с www.znanio.ru