О проблемах внедрения интерактивных методов обучения высшей математике

О ПРОБЛЕМАХ ВНЕДРЕНИЯ В ВУЗЕ ИНТЕРАКТИВНЫХ МЕТОДОВ ОБУЧЕНИЯ В КУРСЕ МАТЕМАТИКИ.

Воробейчикова Е.С. (Мурманск, Мурманский государственный технический университет, кафедра ВМ и ПО ЭВМ, elenavorobeichikova@mail.ru)

The peculiarities of using of interactive methods at practical classes in the subject “Mathematics” at High School are taken into consideration in this article. The author gives some recommendations of methodics, as an example Case's method is given. The factors restraining a wide application of these methods are also analyzed.

Статья посвящена проблемам внедрения интерактивных методов обучения в преподавании математики в ВУЗах.

Необходимость внедрения таких методов диктуется переходом к новым государственным образовательным стандартам (ФГОС) третьего поколения. Согласно ФГОС, «реализация компетентностного подхода должна предусматривать широкое использование в учебном процессе активных и интерактивных форм проведения занятий … с целью формирования и развития профессиональных навыков обучающихся»

Таким образом, внедрение активных и интерактивных форм обучения – одно из важнейших направлений совершенствования подготовки студентов в современном ВУЗе. Основные методические инновации связаны сегодня именно с применением интерактивных методов обучения[1].  Доля занятий проводимых в активной и интерактивной форме по различным специальностям, согласно ФГОС, составляет от 10% до 30%. Прежде чем рассматривать возможности внедрения таких занятий, необходимо выяснить, что подразумевается под понятием “интерактивное обучение”.

В современной педагогической литературе существует некая двойственность относительно данного понятия. С одной стороны, интерактивность в обучении - это характеристика взаимодействия и общения субъектов процесса обучения. С другой стороны – это дидактическое свойство средств обучения (применение электронно-коммуникационных средств). Описание и определение интерактивного обучения в каждом конкретном случае обусловлено авторской трактовкой понятия интерактивности, само же понятие интерактивности разработано слабо[2].

Итак, многие преподаватели достаточно узко подходят к пониманию  “интерактивности”, считая, что достаточно использовать, например, интерактивную доску или компьютер на занятиях по математике и, таким образом, выполнить необходимое процентное соотношение интерактивных занятий.

Приведем некоторые фрагменты из ФГОС, которые позволили нам определить направление внедрения интерактивных методов в преподавании математики в нашем ВУЗе:  “Выпускник должен обладать следующими общекультурными компетенциями (ОК): … способен к работе в коллективе, демонстрирует готовность к сотрудничеству (ОК-5); … способен осуществлять деятельность, связанную с руководством действиями отдельных сотрудников, оказывать помощь подчиненным. Способен на научной основе организовать свой труд, оценить с большой степенью самостоятельности результаты своей деятельности, владеет навыками самостоятельной работы (ОК-6); …способен получать и обрабатывать информацию из различных источников…(ОК-7); владеет культурой мышления, способен к обобщению, анализу, систематизации, постановке целей и выбору путей их достижения, умеет логически верно аргументировано и ясно строить свою речь (ОК-10); способен находить организационно - управленческие решения в нестандартных ситуациях и готов нести за них ответственность… (ОК-11)”.

Таким образом, если ориентироваться на необходимость формирования общекультурных и профессиональных компетенций, то следует трактовать понятие “интерактивность” более широко, нежели только применение электронной техники. Итак, интерактивное обучение предполагает активное вовлечение студента в диалог в качестве активного участника, при этом знание должно добываться в совместной деятельности студентов между собой и преподавателем.

С учетом изложенных представлений об интерактивности в обучении, современных тенденций высшего образования и, опираясь на непосредственное  направления образовательной деятельности (обучение будущих инженеров), изложим основные ключевые позиции внедрения интерактивных методов в обучении математике.

К современным интерактивным технологиям принято относить такие как:  деловые и ролевые игры, кейс-технологии, учебные дискуссии,  мастер-классы, мастерские,  тренинги, метод проектов, программированное обучение, «Мозговой штурм», разработка проекта, решение ситуационных задач.

Из предложенного достаточно большого списка технологий, нами был выбран так называемый case-метод. Выбирая данный метод, мы опирались на следующие факторы:

·         метод позволяет сохранить некоторые принципы обучения математике (приобретение учащимися определенного круга знаний, умение использовать изученные математические методы, развитие математической интуиции, воспитание математической культуры) [3],  

·         метод позволяет устанавливать межпредметные связи, что так же является одной из особенностей  современного процесса обучения математике,

·         метод позволяет формировать общекультурные компетенции.

Методика “case-study” – это методика ситуационного обучения, основанная на реальных примерах, взятых из практики (например, функционирование какого-либо предприятия) и требующая от студента поиска некоторого целесообразного решения в предложенной ему практической ситуации.

Отличительными особенностями кейс–метода являются: описание реальной проблемной ситуации; альтернативность решения задачи; единая цель и коллективная работа по выработке решения; функционирование системы группового оценивания принимаемых решений; эмоциональное напряжение учащихся.

Метод case-технологии является для российской высшей школы одним из самых неразвитых и неотработанных. Учитывая то, что такой вид обучения студентов вообще является нераспространенным, то на занятиях по математике его тем более не используют.  Это объясняется тем, что, например, в гуманитарных дисциплинах и даже в физике новая методика предполагает разрешение группой учеников конкретно поставленной проблемы, которая, по сути, не имеет однозначного решения, то есть, возможны альтернативные, конкурирующие варианты решений. Учащиеся сами предлагают различные способы разрешения поставленной перед ними задачи.  А в математике каждая задача или пример обязательно должны иметь ответ.  Таким образом, одним из самых очевидных недостатков  применения кейсов в математике – это крайне трудный подбор таких тем, где возможны альтернативные решения.

Если обратить внимание конкретно на предмет изучения математики, то многие студенты интересуются вопросом, как именно и в какой мере им понадобятся приобретенные по предмету знания, насколько оправданными станут затраты времени и усилия на изучение такой сложной дисциплины. Таким образом, целью подготавливаемых кейсов с заданиями является разработка рекомендаций по системе подготовки учеников к решению задач определенного типа. Важно так же то, что кейс-метод наглядно демонстрирует необходимость владеть математическими навыками при постановке профессиональных задач.

Технология предполагает от преподавателя математики письменную подготовку примера кейса, его самостоятельное изучение учениками, совместное обсуждение поставленной проблемы (естественно, при руководстве и помощи преподавателя).

В основу кейс-метода ложится имитационное моделирование, то есть приобретение навыков выбора и анализа на математическом примере и перенесение его в реальную профессиональную деятельность.  

В начале занятия с применением кейс-метода студентов разделяют на небольшие группы (по 3-5 человек). При этом в каждой группе должен быть так называемый модератор (наиболее способный студент, который буде руководить процессом, выдвигать и анализировать идеи, предлагаемые группой). Преподаватель наблюдает за процессом, при необходимости задает наводящие вопросы, помогает составить отчет.

В качестве пробного образца нами был предложен кейс по теме “Использование свойств функций, а так же навыков вычислений для расчета времени и температуры тепловой стерилизации продуктов” для специальностей технологического факультета. Данный кейс направлен на закрепление темы “Функции и их свойства и графики”, а так же на закрепление навыков вычисления значений показательной и логарифмической функций (темы рассматриваются в рамках курса  “Основы высшей математики”).

Тип занятия: практическое занятие.

Ведущая цель: обобщить знания, умения, навыки по теме “Функции и их свойства и графики” на примере показательной и логарифмической функции.

Триединая дидактическая цель:

Обучающий аспект: повторить основные формулы и понятия по теме, формировать умение использовать полученные знания при решении задач, укреплять интерес к математике. Развивающий аспект: развитие познавательного интереса, развитие внимания, памяти, развитие эмоциональной сферы. Воспитательный аспект: воспитание культуры поведения, воспитание умения работать в группе, воспитание культуры умственного труда.

Тип кейса: данный кейс, в зависимости от уровня подготовленности аудитории, может быть использован преподавателем как обучающий, развивающий или диагностирующий.

Структура: кейс состоит из трех частей.

1. Теоретическая  часть, сопровождаемая пояснительной запиской. Студентам предлагается войти в роль технологов одного из предприятий, изучить теоретические сведения, необходимые для процесса изготовления консервов и решить поставленные перед ними задачи.

Содержимое кейса. “Консервирование пищевых продуктов при тепловой стерилизации заключается в том, что продукт, уложенный в герметически укупориваемую тару в течение определенного времени подвергается нагреванию. Нужную температуру поддерживают в течение некоторого промежутка времени, затем ее постепенно снижают.

Основные параметры, характеризующие процесс стерилизации: температура и время.

Этими двумя параметрами обеспечивается гибель патогенных микроорганизмов. Несоблюдение этих параметров приводит к возникновению различных видов биологического брака, а именно: газообразование с бомбажем, вздутие крышек, скисание, сплесневение и т.д.

Уничтожение микробов при стерилизации не происходит мгновенно. Для их уничтожения необходимо время, которое называют летальным.

Изучая гибель микроорганизмов под влиянием нагревания, исследователи пришли к выводу, что с физико-химической стороны процессы, вызывающие смерть микробной клетки, представляют собой мономолекулярную реакцию коагуляции белков протоплазмы, и, следовательно, скорость уничтожения микробов поддается математическому анализу.  Количество патогенной флоры убывает по экспоненциальному закону:

         (1)

Здесь  N₀ - количество микроорганизмов к началу стерилизации, N- количество микроорганизмов к концу стерилизации, - время снижения количества пор, К₀-коэффициент скорости уничтожения микроорганизмов.

Если принять ,  то можно получить , а значит (2), что так же подтверждает экспоненциальный характер гибели патогенной флоры под воздействием микроорганизмов.

В самом общем виде положим - начальное количество микрофлоры; -конечное количество микрофлоры.  Время уничтожения патогенной флоры таким образом можно найти по формуле:

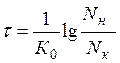   (3)

Если обозначить фактор 1/K₀ через коэффициент D, то  формула (3) примет вид:

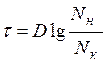  (4)

Здесь  D - это время, требующееся для снижения микроорганизмов в 10 раз. Коэффициент D так же называют временем уничтожения 90% микроорганизмов, оно является константой и предлагается в специальных таблицах” [4].

2. Поставленные задачи.  Набор задач,  связанных с профессиональной деятельностью, решить которые необходимо в рамках данного кейса. Рассматриваются задачи на определение времени стерилизации, количества патогенной флоры к концу стерилизации. Студентам предлагается: объяснить дробное (меньшее единицы) количество микроорганизмов в конце стерилизации, выяснить, возможность полного уничтожения микроорганизмов при стерилизации. Ответы необходимо пояснить, опираясь на свойства математических функций, демонстрирующих данные производственные процессы. Студентам так же предлагается в рамках данного кейса провести работу по графическому анализу процесса стерилизации. Приведем некоторые вопросы и задачи по данному кейсу.

1.                 Если начальное количество спор микроорганизмов 1млн.спор, то сколько потребуется времени для снижения  этого количества до 100 спор, если константа D при данных условиях 4 мин.?

2.                  Сколько времени потребуется для стерилизации при этих же условиях, если начальное количество спор 1 млрд.?

3.                  Определить количество микроорганизмов, которое можно ожидать через 40 минут стерилизации, если их начальное количество составляло 1 млн.?

4.                  Объясните с точки зрения свойств показательной функции дробное (меньшее единицы) количество микроорганизмов в конце стерилизации?

5.                  Возможно ли полное уничтожение микроорганизмов при стерилизации? Поясните ответ, используя  свойства показательной функции.

6.                  Начальное содержание спор в консервах 10⁶. Какой должна быть продолжительность      стерилизации       для конечного содержания спор 10² ,10, 1, 10^-1,10^-2 . Результаты расчета предоставить в виде графика зависимости от N_к.  Константа термоустойчивости D=2 мин.

7.                  Какое количество спор можно ожидать в консервах после стерилизации в течение 24 мин, если их начальное содержание 10⁵.  Константа термоустойчивости D=3 мин.

8.                  Сосчитать ожидаемое содержание спор в продукте после стерилизации в течение 30 мин, если начальное содержание спор 10⁶. Константа термоустойчивости D=2 мин.

3. Отчет о проделанной работе. Результаты, пояснения, обоснования, выводы, которые студенты оформляют на отдельных листах, называемых  протоколами.  Являются основой для оценки результатов деятельности. Подведение итогов.

Преимущества использования данного кейса налицо:

1.       Демонстрирует область применения таких абстрактных для студентов функциональных зависимостей как показательная и логарифмическая.

2.       Демонстрирует необходимость умения проводить  расчеты.

3.       Знакомит студентов с элементами будущей профессии.

4.       Показывает значимость математики для данной специальности.

5.       Развивает умение студентов совместно решать поставленные задачи, работать в команде, помогать друг другу, уважать мнение каждого.

Несмотря на многочисленные плюсы интерактивных технологий, считаем необходимым, обратить внимание на проблемы, которые возникают в ходе их реализации в рамках преподавания математики:

1.       Возрастает нагрузка на преподавателя в процессе подготовки (необходимо вникнуть в содержание специальности, на которой работает преподаватель, проанализировать какие задачи должны уметь решать данные специалисты, проанализировать возможные межпредметные связи, разработать учебный материал в рамках дисциплины “Математика”).

2.       Возможны психологические и коммуникативные трудности  для студентов[5].   Не все студенты достаточно раскрепощены, что бы быть активными при  работе в группе. Более того, некоторые студенты настолько слабо подготовлены по математике в школе, что попросту могут оказаться “ненужными” в группе и испытывать психологический дискомфорт от своей “несостоятельности”.

3.       Проблема переоценки возможностей. Излишне увлекаясь идеей внедрения интерактивных технологий, можно не заметить, что время и силы, потраченные на подготовку, не оправдываются теми результатами, которые мы получаем. Изучить или закрепить можно совсем небольшое количество учебного материала, а времени потратить много.

4.       Технические проблемы. Отсутствие оснащенности кабинетов компьютерами, интерактивными досками значительно усложняет процесс внедрения технологий.

5.       Проблема субъективной оценки. При работе в группе достаточно трудно однозначно оценить работу каждого, то есть налицо проблема индивидуального оценивания знаний.

6.       Принципы системности и научности знаний не реализуются.

7.       Узкий круг тем, которые студенты могут изучать самостоятельно.

8.       Отсутствие альтернативности принятых решений.

Следует так же обратить внимание на общие проблемы внедрения интерактивных технологий (относящиеся не только к преподаванию математики):

·         отсутствие системы целевого повышения квалификации преподавателей по интерактивным методикам преподавания,

·         нежелание имеющихся профессионалов-практиков работать в системе ВПО, вызванное низким уровнем существующей в ней заработной платы,

·         нежелание имеющихся в структуре ВПО преподавателей менять наработанную годами практику преподавания в условиях материальной незаинтересованности [6],

·         большая психологическая нагрузка на преподавателя, который должен быть достаточно эмоциональным в течение всего процесса обучения, разрешать и не допускать конфликты, создавать обстановку сотрудничества и конкуренции одновременно, и самое главное, обеспечивать соблюдение личностных прав студента,

·         проблема междисциплинарной и межкафедральной согласованности применяемых форм обучения.

В заключении следует отметить, что современные методы обучения должны быть направлены на подготовку специалиста, который помимо определенного круга профессиональных знаний и умений, уверенно владеет аналитическим мышлением, эрудицией, умением находить выход из сложной ситуации и многими другими интеллектуальными навыками. Однако, в той части образования, которая связана с математикой, следует быть очень внимательными. Внедряя интерактивные методы в процесс преподавания математики в ВУЗе, следует помнить о том, что математика – фундаментальная наука. Внедрять новые технологии в процесс ее преподавания  следует небольшими порциями, каждый раз соизмеряя затраты и ожидаемые результаты. Не следует полагаться только на эффективность интерактивных методов, применяя их в ущерб традиционным (пассивным). Успешность преподавания математики в ВУЗе определяется умением выбрать их оптимальное количественное  соотношение в рамках лекций и практических занятий.

Следует так же отметить, что работа по внедрению интерактивных методов на нашей кафедре находится в начальной стадии. Планируется изучение, разработка и внедрение не только кейс-методов, но и других методик с целью изучения их эффективности и проблем их внедрения в процессе преподавании математики в ВУЗах. 

ЛИТЕРАТУРА.

1.  Анацкая А.Г. Интерактивные методы обучения. // Инновационное образование и экономика.-2011.-№9.-С.44-48.

2. Гавронская Ю. “Интерактивность” и “интерактивное обучение”. // Высшее образование в России. -2008.-№7.-С.101-104.

3.  Кудрявцев Л.Д. Современная математика и ее преподавание. - М.: Наука, 2010.

4. Куцакова В.Е. и др. Примеры и задачи по холодильной технологии пищевых продуктов. Теоретические основы консервирования. – Санкт-Петербург.: ГИОРД, 2008.

5. Рыбакова Т. Психологический потенциал интерактивных методов. //Высшее образование в России. -2004.-№12.-С.41-44.

6. Фурс М.В. Интерактивные формы обучения - средство повышения уровня профессиональной подготовки студентов. // Педагогика и психология. -2011.-№10.-С.29-32.