О ВЫВОДЕ ФОРМУЛ СЛОЖЕНИЯ И ВЫЧИТАНИЯ УГЛОВ, ОСНОВАННОМ НА РАССМОТРЕНИИ ПЛОЩАДЕЙ

О ВЫВОДЕ ФОРМУЛ СЛОЖЕНИЯ И ВЫЧИТАНИЯ УГЛОВ, ОСНОВАННОМ НА РАССМОТРЕНИИ ПЛОЩАДЕЙ

В изложении этого вывода формул сложения и вычитания углов авторы статей и учебника пользуются тригонометрическим выражением площади треугольника через две его стороны и синусом угла, заключенного между ними. В настоящей статье приводится другой вариант того же вывода, — в нем тригонометри­ческая формула площади треугольника не при­меняется.

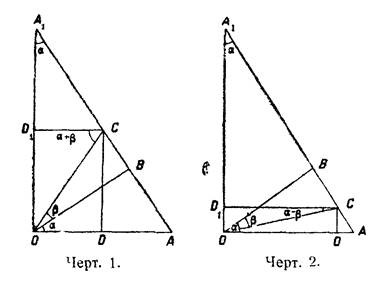
Пусть в треугольнике АОС (см. черт 1 и 2) ˪АОВ = α, ˪ВОС = β, OB ┴ AC и CD ┴ AO.

Из чертежа видно, что пл. ∆АОС = пл. ∆АОВ ± пл. ∆ВОС, откуда

AO·CD = AB·BO ± ВО·ВС,

Но так как:

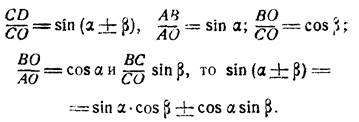
Восстановим в вершине О треугольника АОС перпендикуляр к АО. Пусть он пересе­чет продолжение стороны АС в точке А₁. Проведем CD₁┴А₁O, тогда  ˪А₁ = α и

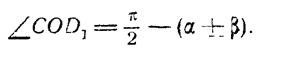
Замечая, что пл. ∆ А₁ОС = пл. ∆ А₁ОВ ± пл. ∆ ВОС, аналогично предыдущему получим:

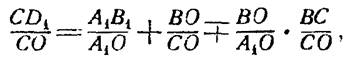
откуда cos(α±β) = cosα cos β ± sinαsinβ.

Выше         предполагалось,  что    α±β < 90°.

Распространение на α±β > 90° легко сде   лать, но тогда пришлось бы пользоваться формулами приведения.

Скачано с www.znanio.ru