Объемы тел

Анализируя задания на нахождение объемов тел в учебнике  Атанасян Л.С.  Геометрия для 10-11 классов, можно прийти к выводу, что подборка задач не соответствует тематике задания В11 в ЕГЭ.

По статистике задание В11 выполняют от 20% до 40% выпускников. И все зависит от того, какая из задач попадется. Ни а какой равноценности и равнозначности задач не может идти речь. Все дело в том, что задачи на нахождение объемов фигур проверяют уровень развития пространственных представлений о многогранниках, круглых телах и их комбинаций. Для успешного выполнения задач требуется знание основных формул, умение проводить дополнительные построения на изображениях пространственных фигур, работать с формулами, выполнять арифметические действия и преобразования числовых выражений.

В данной разработке представлены задачи от самых простых до более сложных. К задачам представлено подробное решение.

Данный материал может использоваться учителем как на уроке, так и на консультациях для учеников, которым близка тема В11.

Задачи:

Тип 1 ( простые)

1.Диаметр основания конуса равен 12, а длина образующей – 10. Найдите объем конуса. В ответе запишите  .

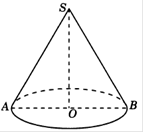
Решение:

Ответ: 96.

2. Ребра прямоугольного параллелепипеда равны 4, 5 и 8. Найдите объем параллелепипеда.

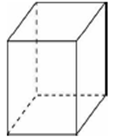
Ответ:160

3. Радиус основания цилиндра равен 4, высота  . Найдите объем цилиндра.

Ответ:160

4. В основании треугольной пирамиды лежит прямоугольный треугольник с катетами 4 и 3. Найдите объем пирамиды, если её высота равна 9.

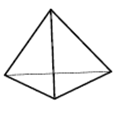
Ответ:18

5. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту конуса пополам. Найдите объем отсеченного конуса.

Способ 1.

Линейные размеры большого конуса . Линейные размеры маленького конуса  и  .

Преобразуем:

Подставим:

Ответ:1,5  - сложно

Способ 2.

Подсказка:

При изменении всех линейных размеров тела в k раз, объем  этого тела изменяется в раз.

Ответ:1,5

Данный прием решения задач не требует знания формулы объема конуса.

6. Коническая воронка объемом 16 литров полностью заполнена жидкостью. Из воронки вычерпали часть жидкости, при этом ее уровень снизился до половины высоты воронки. Сколько литров жидкости вычерпали?

Найдем  сколько литров  жидкости вычерпали:

16-2=14

Ответ:14

7.В сосуд в виде конуса налита жидкость до    высоты. Объем налитой жидкости равен 5. Сколько жидкости нужно долить, чтобы наполнить сосуд доверху?

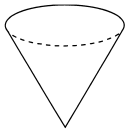
Найдем  сколько жидкости нужно долить, чтобы наполнить сосуд доверху:

320-5=315

Ответ:315

8. Объём прямоугольного параллелепипеда равен 108. Чему будет равен объём параллелепипеда, если каждое его ребро уменьшить в три раза?

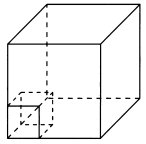
Ответ: 4

9. Объём цилиндра равен 30. Чему равен объём конуса с таким же основанием и высотой?

Подсказка:

Если цилиндр и конус имеют общее основание и высоту, то  

Ответ:10

10. Объём конуса равен 25. Чему равен объём цилиндра с таким же основанием и высотой?

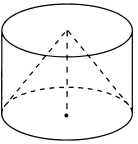
Ответ:75

Тип 2

1. Четырехугольная пирамида весом 81  горизонтальными плоскостями разрезана на 3 части

одинаковой высоты. Найдите вес  средней части пирамиды.

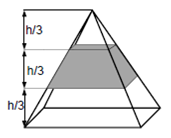
При решении данной задачи можно использовать подсказку из задачи №5 типа 1.

Найдем массу  части пирамиды состоящей из двух частей ( верхняя и средняя ):

Найдем массу  верхней части пирамиды

Найдем  вес средней части пирамиды:

24-3=21

Ответ: 21

2.Найдите объем части куба

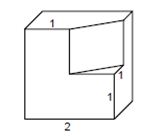
Для того чтобы найти объем части куба. Необходимо из объема всего куба вычесть объем призмы в основании которой лежит равнобедренный прямоугольный треугольник.

Ответ: 7,5

3. Куб описан около цилиндра объемом 16. Найдите объем куба.

Так как цилиндр вписан в куб, то диаметр цилиндра и высота равны ребру куба.

Для цилиндра   

Ответ: 64

4. Основанием прямой призмы является ромб с диагоналями 2 и 6. Найдите объем цилиндра, вписанного в эту призму, если объем призмы равен  .

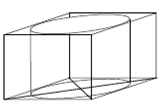
Задача многоэтапная и требует знание не только формул объемов тел.

1.

    , где   по теореме Пифагора

3.=0,45

Ответ: 0,45

5. Объем раствора в гальванической ванне равен 3 куб. м, при этом уровень раствора достигает высоты 75 см. В ванну погрузили деталь, после чего уровень раствора поднялся на 2 см. Найдите объем детали (в куб. м).

За основу берется формула 

Объем раствора в гальванической ванне можно найти по формуле:

Объем детали погруженную  в эту же ванную находим по этой же формуле:

Сделаем необходимые преобразования:

Из первой формулы  и подставим во вторую

Ответ: 0,08

6. В цилиндрический сосуд налили 3000 см³ воды. Уровень воды при этом достиг высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 3 см. Чему равен объем детали? Ответ выразите в см³

При решении данной задачи можно воспользоваться  утверждением: Объем налитой воды в сосуд прямо пропорционален уровню ( высоте ) воды в данном сосуде, при условии, что  величина постоянная.

3000 см³ – 20 см

   х см³   -   3 см

х = (3000∙3):20

х = 450

Ответ:450

7. Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 3,6 раза. Во сколько раз увеличится объем цилиндра?

Решение данной задачи сводится к работе с формулами.

Измерение первого цилиндра                                              Измерения второго цилиндра

Найдем отношение   

Ответ: 2,5

8.. Вершины многогранника являются центрами граней куба. Найдите объем куба, если объем многогранника равен 12.

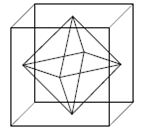
Обозначим ребро куба через .

Многогранник составлен из двух равных пирамид имеющих общее основание.

, то есть

, где  , а  , где сторона основания равна .

Подставим в формулу

Так как , то

Ответ: 72

9. В конус объемом 36 вписан шар. Найдите объем шара, если осевое сечение конуса является равносторонним треугольником.

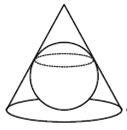
Использовать будем две формулы:   и 

Так как осевое сечение конуса является равносторонний треугольник со стороной   , то

   , а . Тогда   .

Подставим в формулу  и упростим:

Подставим в формулу  и упростим:

Исходя из того, что

Ответ:16

10. В правильную треугольную призму объемом    вписан шар. Найдите радиус шара.

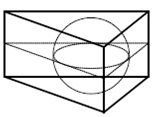
Выразим объем призмы, используя формулу: , где

Используем решение предыдущей задачи.

Подставим в формулу объема призмы

Теперь найдем :

Ответ: 1,5

Источники информации:

1. «Геометрия, 10-11» Учебник для общеобразовательных учреждений. Л. С. Атанасян, И. Ф. Бутузов, С. Б. Кодомцев и др. М.: Просвещение.2010.

2.Изучение геометрии в 10-11 классах: кн. для учителя /С.М.Саакян, В.Ф.Бутузов.- 4-е изд., дораб.- М.: Просвещение. 2010.

3. ЕГЭ 2012. Математика. Задача В11. Стереометрия: объемы и площади. Рабочая тетрадь / Под ред. А.Л.Семенова и И.В.Ященко.-М.: МЦНМО, 2012.

4. Тексты  КДР 2010-2013 г . Автор составитель:  Краснодарский краевой институт дополнительного профессионального педагогического образования.

5.2012 ФГБУ « Федеральный центр тестирования»  WWW.RUSTEST.RU

ФГБНУ « Федеральный институт педагогических измерений»  WWW.FIPI.RU

Скачано с www.znanio.ru