Обобщающий урок по теме: "Тела вращения. их объемы, площади поверхностей.

ГОУ РК РЦО УКП «Верхний Чов»

Конспект урока.

Преподаватель математики и информатики и ИКТ Вавилина  Любовь Васильевна.

Тема урока: « Тела вращения, их объемы и площади поверхностей».

Тип урока: урок – конкурс, на котором используется групповая форма работы.

Цели урока:

Образовательная: проверка усвоения изученного материала,                                                                                                       умения применять теоретический материал для решения практико-ориентированных задач связанных с конусом, шаром, цилиндром.

Развивающая: развитие конструктивных способностей учащихся; каждый учащийся борется за личное и командное первенство.

Воспитывающая: воспитывать волю к победе, любовь к профессии, фантазию.

Средства обучения:

 Технические:  мультимедийная система, интерактивная доска.

 Художественно-изобразительные (цифровые материалы): электронная презентация к конкурсу капитанов и к историческому конкурсу «Тела вращения».

Оборудование:  демонстрационная полка с телами вращения, модели фигур вращения (цилиндр, конус, шар), раздаточный материал таблицы-задания, шарикоподшипники, роликовые подшипники, глобус,  линейки, карандаши.

Метод обучения: объяснительно-иллюстративное повторение пройденного материала.

Межпредметные связи: физика «Поверхностное натяжение», астрономия «Солнечная система», география «Параллели и меридианы», черчение «Разрез поршня ДВС».

Ход  урока:

 1. Организационный момент:

 а) Рапорт о готовности к уроку.

 б) Проверка принадлежностей у всех учащихся.

 в) Объяснить ход урока и его цели:

Ребята, сегодня у нас урок – конкурс по теме: «Тела вращения, их объёмы и площади поверхностей». Вам предстоит участвовать в конкурсах: конкурс капитанов; разминка команд; практический конкурс; исторический конкурс; конкурс – «гимнастика ума», где вы будете применять изученный материал и бороться как за личное, так и командное первенство.

Мое пожелание:   Если что-то непонятно,

                                  Это очень неприятно.

                                  Пусть тоска тебя не гложет,

                                 Рядом друг, и он поможет.

 2. Конкурсные задания:

     Конкурс капитанов:

На демонстрационной полке вы видите модели. Определимся с названием команд, таким образом, капитаны команд выберут тело вращения, которое будет соответствовать названию команды и дадут ему характеристику. Ответы капитанов оцениваются учащимися команд соперников и преподавателем по пятибалльной системе, и выводится средний балл, который будет занесён в лицевой счёт.

 (на доске)

ЦИЛИНДР

1. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом и отрезков, соединяющих соответствующие точки кругов.

Круги – основания цилиндра.

Отрезки – образующие цилиндра.

 ВС – радиус (радиусом цилиндра называется радиус его основания).

АВ – высота (высотой цилиндра называется расстояние между плоскостями его оснований). Ось цилиндра (осью цилиндра называется прямая, проходящая через центры оснований).

2. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

3. Цилиндр – тело, полученное от вращения прямоугольника вокруг его стороны как оси.

4. Сечение, проходящее через ось, называется осевым.

5. Сечение, перпендикулярное оси – круг.

6.  S_б.=C∙H;                S_nn=2∙S_осн.+S_бок.;          V=S_осн.∙Н;

     S_б. =2R∙H;          S_nn=2R²+2RH;          V=R²∙H.

     R – радиус цилиндра, Н – высота. Поверхность цилиндра состоит из         оснований и боковой поверхности.

КОНУС

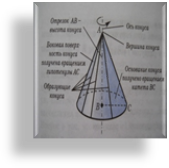
1.           Конусом называется тело, которое состоит из круга (основания конуса), точки, не лежащей в плоскости круга (вершины) и всех отрезков, соединяющих вершину с точками основания (образующих).

2.            Высотой конуса называется перпендикуляр, опущенный из

 его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.

3.            Конус – тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.

4.            Сечение конуса плоскостью, проходящей через ось, называется осевым сечением. Осевым сечением конуса является равнобедренный треугольник.

5.            Сечение, перпендикулярное оси конуса – круг.

6. Плоскость, перпендикулярная оси, отсекает меньший конус. Оставшаяся часть – усечённый конус.

 7.  Поверхность конуса состоит из основания и боковой поверхности:

S_nn=S_осн.+S_бок.;  S_nn=R²+RL;  V=R²H.

ШАР

1.                   Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара.

2.                  Граница шара называется шаровой поверхностью или сферой.

3.                  Точки сферы – это точки шара, удалённые от центра на расстояние равное радиусу.

4.                  Отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом.

5.                  Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара – диаметр.

6.                  Концы любого диаметра называются диаметрально противоположными точками шара.

7.                  Шар, получается, от вращения полукруга вокруг диаметра как оси.

8.                  Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

9.                  Плоскость, проходящая через центр шара, называется диаметральной плоскостью.

10.               Сечение шара диаметральной плоскостью называется большим кругом. Сечение сферы – большой окружностью.

11.        Площадь сферы:  S=4R², где R – радиус сферы.

12.               Объём шара:  V=πR³, где R – радиус шара.

 

 

Разминка команд:

Переходим к конкурсу: «Разминка команд». На доске таблица с рисунками тел вращения. На столах перед вами такие же таблицы – задания. Необходимо подписать свою фамилию и  заполнить пустые клетки, кроме последней.

Оценка результатов: (будет дана по схеме)

- если в строке верны все ответы – 4 балла

- если в строке верны 3 ответа – 3 балла

- если в строке верны 2 ответа – 2 балла

- если в строке верен 1 ответ – 1 балл

 

Вывод: Каждый участник может принести своей команде 12 баллов, если в каждой строке верны все ответы.

Приступим к выполнению.

НАЗВАНИЕ	ТЕЛО ВРАЩЕНИЯ	ПРИ ВРАЩЕНИИ КАКОЙ ФИГУРЫ ПОЛУЧАЕТСЯ	ПОЛНАЯ ПОВЕРХНОСТЬ	ОБЪЁМ	БАЛЛЫ
Шар		Полукруга вокруг диаметра	S=4πR2	V=πR3
Конус		Прямоуголь-ного треуголь- ника	S=πR2+πRL	V=πR2H
Цилиндр		Прямоуголь-ника	S=2πR2+2πRH	V=πR2H
Усечен- ный  конус		Прямоуголь-ной трапеции	S=Lπ(R1+R2)+ +πR12+πR22	V=πH(R12+ R1∙R2+R22)

                Ф. И.    учащегося

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заканчиваем работу.

Проверим правильность ваших ответов. Открываем первую строку, баллы подсчитывает у себя каждый и сообщает капитану для записи в лицевой счёт команды, аналогично все последующие строки.

Практический конкурс:

Каждой команде дана задача для самостоятельного решения. Учащиеся могут набрать дополнительные баллы, если решив свою задачу, решат ещё и задачу противника.

Команда «ШАР»	Команда «ЦИЛИНДР»	Команда «КОНУС»
Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4м и диаметром 20см, если на швы необходимо добавить 2,5% площади ее боковой поверхности.	Конусообразная палатка высотой 3,5м и диаметром основания 4м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку, если 5% материала ушло на швы и отходы.	Верхняя часть башни имеет форму полушара, радиус которого м. Верхнюю часть башни планируется покрыть мозаикой. Сколько мешков клея потребуется купить для этой работы, если расход клея 6кг на 1м² и в одном мешке 30кг клея?

 

Оценка результатов:

«5» - решение и чертёж выполнены верно.

«4» - ошибка при нахождении числа по его %.

«3» - ошибка в вычислениях, не определены S_бок. или V_м.

«2» - незнание формул, следовательно, неверное решение.

Подписываем листочки. Оформляем решение соответствующей задачи. Представители команд выйдут по мере готовности, расскажут ход решения и результаты вычислений.

Команда «ШАР»

                                                                                                                Дано:

Цилиндр

d = 20 см

H = 4 м

2,5% на швы

Найти:

S_бок.п + 2,5% S_б.п.

Решение:

Sбок_. = 2πRH = 2 × 3,14 × 10 × 400 = 25120 (см²)

25120см²÷ 100%∙ 2,5% = 628 (см²)

S_бок.п + 2,5% S_б.п. = 25120 + 628 = 25748 см²≈ 2,58 м²

Ответ: На изготовление трубы необходимо 2,58 м² .

Команда «ЦИЛИНДР»

Дано:

Конус

d = 4 м

5% на швы

Найти:

S_{бок. к.} + 5% S_{парусины}

                   Решение:

S_{бок. к} = πRL

SA = L. Из ∆SOA по т. Пифагора найдем

 SA =   SO² + AO² =   16,25

S_{бок. к} = 3,14 × 2  16,25 ≈  25 м²

25 м² – 95%

X – 100%

X = 25×100÷95 ≈ 26,3 (м²)

Ответ: Для палатки необходимо 26,3 м² парусины.

Команда «КОНУС»

 

Дано:

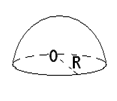Полушар

R=6/√π м

На 1 м²- 6кг клея

1 мешок – 30кг клея

Найти:

 n- мешков

Решение:

S = ½∙4πR² = 2πR² = 2π∙36/π = 72 (м²)

72∙6 = 432 (кг)

n = 432÷30 = 14,4 мешка ≈15 мешков

Ответ: 15 мешков.

Исторический конкурс:

От каждой команды по одному человеку должны рассказать историю возникновения, применения тела вращения, название которого носит команда. (Оценка по пятибалльной системе)

Конкурс - «гимнастики ума»:

1.                  Из каких фигур состоит развёртка цилиндра.

2.                  Может ли осевым сечением конуса быть прямоугольный треугольник?

3.                  Как необходимо расположить фигуры, чтобы шар был справа от цилиндра, но слева от конуса.

4.                  У цилиндра радиус равен 2см, высота 3 см, найти диагональ осевого сечения. (5)

5.                  Высота конуса равна радиусу основания. Найти угол при вершине осевого сечения.

6.                  Объём шара уменьшили в 8 раз, как изменилась его поверхность? (в 4 раза меньше)

           3. Подведение итогов:

            Чему научились?

Оценки за урок:

23 балла и более – «5» («молодец»)

От 20 до 22 баллов – «4» («так держать»)

От 15 до 19 баллов – «3» («подтянись»)

Ниже 15 баллов – «2» («должно быть стыдно»)

Награждение групп переходящими вымпелами по номинациям:

- самая быстрая группа;

- самая активная группа;

- самая эмоциональная группа;

- группа, соблюдающая правила работы в группе.

 

4. Домашнее задание:

   Изготовить модели конуса и цилиндра, вычислить их полную поверхность.