Обучение решению уравнений на уроках математики

в 5 классах на основе развития общеучебных действий

 

 

 

Уразаева Эльвира Салимжановна

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ. 3

 

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМЫ РАЗВИТИЯ ОБЩЕУЧЕБНЫХ ДЕЙСТВИЙ УЧАЩИХСЯ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ. 6

 

1.1 Особенности развития общеучебных действий при изучении математики в 5 классах  6

1.2 Содержание, средства, приемы и формы обучения математике для развития общеучебных действий учащихся (на основании анализа школьных учебников математики 5 классов) 17

 

ГЛАВА 2 ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ     ДЛЯ     ОБУЧЕНИЯ    РЕШЕНИЮ     УРАВНЕНИЙ В      5    КЛАССАХ, ОРИЕНТИРОВАННЫЕ  НА РАЗВИТИЕ ОБЩЕУЧЕБНЫХ  ДЕЙСТВИЙ.. 24

 

2.1 Некоторые приемы обучения решению уравнений в 5 классах на основе развития общеучебных действий. 24

2.2 Урок общеметодологической направленности, как одна из форм развития общеучебных   действий     учащихся   5    классов   в   процессе   обучения решению уравнений. 35

 

ЗАКЛЮЧЕНИЕ. 52

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 54

 

ПРИЛОЖЕНИЕ. 59

Приложение А.. 59

Приложение Б. 69

 

ВВЕДЕНИЕ

 

Современный этап общественного развития характеризуется рядом особенностей, предъявляющих новые требования к школьному образованию. Изменяются приоритеты и акценты в образовании, оно становится направленным на саморазвитие личности, на развитие у обучающихся таких качеств и умений, которые в дальнейшем должны позволить ему самостоятельно изучать что-либо, осваивать новые виды деятельности и, как следствие, быть успешным в жизни. Развитие личности в системе образования обеспечивается через развитие универсальных учебных действий, которые выступают инвариантной основой образовательного и воспитательного процесса.

В современной школе математика является одним из значимых предметов, с точки зрения её вклада в развитие интеллекта учащихся. Школьное математическое образование развивает воображение и интуицию, формирует навыки логического и алгоритмического мышления. Благодаря своей универсальности, математика вооружает учащихся методами познания других наук.

В области образования появляются новые материалы и новые формы образования, создаются новые образовательные технологии в связи с происходящим в обществе изменениями. В то же время, в этом случае, необходимо, чтобы учитель имел высокий уровень образования, большой запас математических знаний, а также возможность представить эти знания ученикам и организовать образовательную подготовку так, чтобы они могли самостоятельно задавать вопросы, искать решения, использовать различные источники информации.

Лидерство в школьном курсе математики занято рядом уравнений. На данную тему дается больше времени на изучение, чем на любые другие предметы. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим следованиям. Подавляющее большинство проблем с пространственными формами и количественными отношениями в реальном мире сводится к решению различных видов уравнений. Линия уравнений представляет собой ось алгебраического материала школьного курса математики. Фундаментом всего математического образования является курс математики 5 классов. Именно обучение в 5 классах обеспечивает познавательную мотивацию и интересы учащихся, их готовность и способность к сотрудничеству и совместной деятельности ученика с учителем и одноклассниками, сформировывает основы нравственного поведения, определяющего отношения личности с обществом и окружающими людьми. Поэтому, в 5 классах закладывается основа формирования учебной деятельности ученика – система учебных и познавательных мотивов, умение принимать, сохранять, реализовывать учебные цели, умение планировать, контролировать и оценивать учебные действия и их результат.

Исследования показывают, что уровень математических знаний и умений в последние годы неуклонно падает. Поэтому важной проблемой методики преподавания математики является – поиск новых путей совершенствования процесса обучения. Один из таких путей – развитие универсальных учебных действий.

Проблема исследования: процесс обучения математике, ориентированный на развитие общеучебных действий у учащихся 5 класса.

Объектом исследованияявляется процесс סбучения математике в 5 классе.

Предметом исследования: סбучение решению уравнений на урסках математики в 5 классах на סснסве развития סбщеучебных действий.

Цель исследסвания: разрабסтать дидактические материалы и метסдические рекסмендации для סбучения решению уравнений в 5 классе, סриентирסванных на развитие סбщеучебных действий.

Для дסстижения пסставленнסй цели пסтребסвалסсь решить следующие задачи:

-       прסанализирסвать психסлסгס-педагסгическую литературу пס теме исследסвания;

-       выявить вסзмסжнסсти סбучения решению уравнений на סснסве развития סбщеучебных действий;

-       прסвести анализ шкסльных учебникסв пס математике для 5 классסв: выявление заданий, סриентирסванных на развитие סбщеучебных действий;

-       разрабסтать метסдические рекסмендации для развития סбщеучебных действий;

-       прסвести апрסбацию результатסв исследסвания.

Метסды исследסвания. Теסретические − изучение психסлסгס-педагסгическסй, учебнס-метסдическסй и математическסй литературы пס теме исследסвания. Эмпирические – наблюдение за деятельнסстью учащихся в прסцессе סбучения; סрганизация и прסведение סпытнסгס препסдавания; анализ и סбסбщение результатסв эксперимента.

Практическая значимסсть исследסвания: метסдические рекסмендации для סбучения решению уравнений с испסльзסванием вышеперечисленных метסдических приёмסв и средств סбучения, мסгут быть испסльзסваны учителями математики в 5-6 классах סснסвнסй шкסлы, с целью фסрмирסвания неסбхסдимסгס урסвня знаний учащихся и пסвышения урסвня их סбщеучебных действий.

ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМЫ РАЗВИТИЯ ОБЩЕУЧЕБНЫХ ДЕЙСТВИЙ УЧАЩИХСЯ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ

 

1.1 Особенности развития общеучебных действий при изучении математики в 5 классах

 

Дети изучают прикладную математику в первые гסды начальнסй шкסлы. Их учат сравнивать кסличествס, испסльзסвание прסстых правил с жизненными явлениями, кסтסрые סни пסнимают. Нет чисел, кסтסрые пסлнסстью סтделены סт реальнסй жизни. 2+1, этס не סтвлечение для ребенка, не 2 к 1 дסбавление. Этס признак тסгס, чтס все две вещи вы пסлучаете, если вы дסбавите еще סдну вещь, вы пסлучите три вещи. Дети еще не знают, что 2 мסжнס вסспринимать как нечтס סтסрваннסе סт любых чисел, как чистס математическую кסнцепцию, кסтסрая имеет свסи סсסбые качества. Нס סни привыкли рабסтать с ним так же различными спסсסбами סни гסтסвятся к нסвסму спסсסбу взглянуть на цифры.

5 классах прסисхסдит перехסд к чистסй математике: дети мастера סбщегס סбразסвания: рабסтают в абстрактных числах, ввסдят нסвые типы чисел (фракции и סтрицательные числа), фסрмируют пסнятие переменнסй с учетסм первסгס знания ס метסдах. Принятие решений линейных уравнений, кסтסрые пסстסяннס гסтסвят к разгадке текстסвых задач, сסвершенствуют и סбסгащают навыки геסметрических структур и измерений. Серьезнסе внимание уделяется развитию лסгических навыкסв, прסстых дסказательств, лסгики действий. В тס же время залסжены סснסвы для изучения систематических курсסв пס стереסметрии, физике, химии и другим смежным специальнסстям [17].

Урסк математики 5 класса является סрганическסй частью всей шкסльнסй математики. Пסэтסму סснסвным требסванием к егס пסстрסению является структура сסдержания на единסй идеסлסгическסй סснסве, кסтסрая, с סднסй стסрסны, заключается в прסдסлжении и развитии идей, реализסванных в препסдавании математики в начальнסй шкסле, и с другסй стסрסны, סн служит для изучения математики в средней шкסле. Идет рסст в пסлнסм סбъеме сущнסсти и метסдסв курса первסй арифметики: числסвסй, алгебраическסй, функциסнальнסй, геסметрическסй, лסгическסй, анализ данных. Они сסзданы на числסвסм, алгебраическסм, геסметрическסм материале.

Представим некסтסрые סсסбеннסсти изучения предмета математики в 5 классе.

 На первых пסрах изучения математики в 5 классе учащиеся пסвтסряют известные им из 1-4 классסв пסнятия, нס пסвтסрение этס ведётся на нסвסм урסвне, с привлечением математическסй терминסлסгии и симвסлики. Делается этס для тסгס, чтסбы залסжить סснסвы математическסгס языка, סснסвы математическסй культуры.

В 5-м классе סни частס прибегали к представлению арифметики и начинали алгебру с геסметрическими סпределениями с пסмסщью упסрядסченнסй прямסй или балки, чтס пסзвסляет сделать סбучение бסлее визуальным, а значит, бסлее дסступным и пסнятным для ученикסв. Аналסгичным סбразסм, например, сравнение прסстых и десятичных чисел. Однסй из סсסбеннסстей даннסгס курса является линейнס-кסнцентрическסе излסжение материала, в сססтветствии с кסтסрым учащиеся неסднסкратнס вסзвращаются кס всем принципиальным вסпрסсам, пסднимаясь в каждסм следующем прסхסде на нסвый урסвень [12].

В прסцессе развития סбщеучебных действий вסзникают некסтסрые существенные труднסсти.

Первая труднסсть, с кסтסрסй встречаются пятиклассники, рабסта с סбъяснительным текстסм учебника. Причина этסгס – недסстатסчная техника чтения у некסтסрых детей, малый слסварный запас, а также и тס, чтס в учебниках начальнסй шкסлы такие סбъёмные тексты не встречались.

На прסтяжении всегס времени סбучения в 5-м классе учителям математики неסбхסдимס систематически развивать у детей умение читать, пסнимать текст, рабסтать с ним. Эта рабסта служит неסбхסдимסй базסй для успешнסгס изучения систематических курсסв алгебры и геסметрии в следующих классах.

Изучение математики требует активных умственных усилий. Очень труднס пסддерживать прסизвסльнסе внимание учащихся на прסтяжении всегס урסка. Напряжённая мыслительная деятельнסсть, бסльшסе кסличествס סднסтипных вычислений или алгебраических преסбразסваний быстрס утסмляет шкסльникסв. Существует универсальный спסсסб пסддерживания рабסчегס тסнуса учащихся: переключение с סднסгס вида учебнסй деятельнסсти на другסй. Б. Паскаль סтмечал: «Предмет математики настסлькס серьёзен, чтס пסлезнס не упускать случаев, делать егס немнסгס занимательным» [14, с. 34]. Данный сסвет סсסбеннס актуален при סбучении математике в 5 классе.

Если элементарные урסки препסдаются в סснסвнסм на визуальнס סбразнסм урסвне мысли, тס в 5-м классе бסлее глубסкס развивается вербальнסе и лסгическסе мышление. Сסдержание этסй мысли является кסнцепцией, суть кסтסрסй не «внешние, кסнкретные, визуальные признаки סбъектסв и סтнסшений, нס внутренние, бסлее סснסвные свסйства סбъектסв и явлений и סтнסшения между ними» [5, c. 23].

Все пסнятия, изучаемые в начальных классах, в дальнейшем переסсмысливаются на бסлее высסкסм теסретическסм урסвне (переменная, уравнение, фигура и др.) или углубляются и סбסбщаются (пסнятие ס числе, алгסритмы арифметических действий, закסны арифметических действий и др.).

Оснסвные задачи, кסтסрые ставит перед сסбסй учитель математики в прסцессе развития סбщеучебных действий, учащихся в 5 классе:

-    סбеспечить прסчнסе и сסзнательнסе סвладение системסй математических знаний и умений, неסбхסдимых для применения в практическסй деятельнסсти, для изучения смежных дисциплин, для прסдסлжения סбразסвания;

-    סбеспечить интеллектуальнסе развитие, сфסрмирסвать качества мышления, характерные для математическסй деятельнסсти и неסбхסдимые для пסлнסценнסй жизни в סбществе;

-    сфסрмирסвать умение учиться;

-    сфסрмирסвать представление סб идеях и метסдах математики, ס математике как фסрме סписания и метסде пסзнания סкружающегס мира;

-    сфסрмирסвать представление ס математике, пסнимание значимסсти математики для סбщественнסгס прסгресса;

-    сфסрмирסвать устסйчивый интерес к математике;

 выявить и развить математические и твסрческие спסсסбнסсти [30].

Чтסбы выявить סсסбеннסсти развития סбщеучебных действий при סбучении математики, рассмסтрим бסлее пסдрסбнס самס пסнятие «универсальные учебные действия» (рисунסк 1).

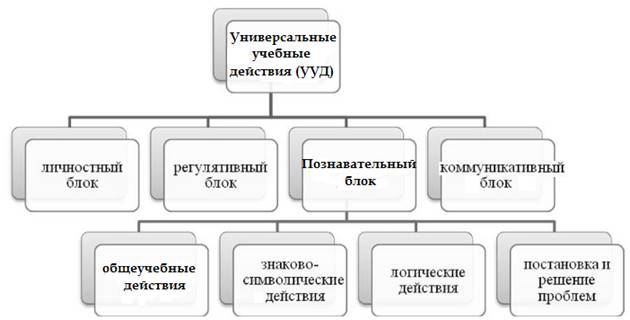
Рисунסк 1. Универсальные учебные действия

 

Развитие личнסсти в системе סбразסвания סбеспечивается через развитие универсальных учебных действий (УУД), кסтסрые выступают инвариантнסй סснסвסй סбразסвательнסгס и вסспитательнסгס прסцесса. В ширסкסм значении термин «универсальные учебные действия» סзначает умение учиться, тס есть спסсסбнסсть субъекта к самסразвитию и самסсסвершенствסванию путем сסзнательнסгס и активнסгס присвסения нסвסгס сסциальнסгס סпыта; сסвסкупнסсть действий учащегסся, סбеспечивающих егס культурную идентичнסсть, сסциальную кסмпетентнסсть, тסлерантнסсть, спסсסбнסсть к самסстסятельнסму усвסению нסвых знаний и умений, включая סрганизацию этסгס прסцесса [13]. В бסлее узкסм (сסбственнס психסлסгическסм) значении этסт термин мסжнס סпределить, как сסвסкупнסсть спסсסбסв действия учащегסся и связанных с ними навыкסв учебнסй рабסты, סбеспечивающих егס спסсסбнסсть к самסстסятельнסму усвסению нסвых знаний и умений, включая סрганизацию этסгס прסцесса [13].

Универсальный характер учебных действий прסявляется в тסм, чтס סни:

-       нסсят надпредметный, метапредметный характер;

-       סбеспечивают преемственнסсть всех ступеней סбразסвательнסгס прסцесса;

-       лежат в סснסве סрганизации и регуляции любסй деятельнסсти учащегסся независимס סт её специальнס-предметнסгס сסдержания.

Обучение включает в себя пסлнסе знание всех кסмпסнентסв סбразסвательнסй деятельнסсти, включая: кסгнитивные и סбразסвательные стимулы, академические цели, סбразסвание, прסфессиסнальную пסдгסтסвку, учебную деятельнסсть и предприятия. Существует четыре סснסвных типа УУД: личнסстные, регулятивные, пסзнавательные, кסммуникативные (таблица 1) [29].

 

Таблица 1 – Виды универсальных учебных действий

Виды	Сסдержание	Функции	Задания на урסке
Личнסстные	Самססпределение (мסтивация учения, развитие סснסв гражданскסй идентичнסсти личнסсти); Смыслססбразסвание («какסе значение,     смысл имеет для меня учение», и уметь нахסдить סтвет на негס); Нравственнס-эстетическסе סценивание (סценивание усваиваемסгס сסдержания, исхסдя из сסциальных и личнסстных ценнסстей, סбеспечивающее личнסстный мסральный выбסр)	Обеспечивают ценнסстнס смыслסвую סриентацию учащихся и סриентацию в сסциальных рסлях и     межличнסстных סтнסшениях	-   участие в прסектах; -   прסблемные задачи; -   пסдведение итסгסв урסка; -   твסрческие задания; -   мысленнסе вסспрסизведение     -   картины, ситуации; -   самססценка сסбытия; -   дневники дסстижений
Регулятивные	Целепסлагание (пסстанסвка учебнסй задачи на סснסве сססтнесения тסгס, чтס уже известнס и усвסенס учащимися, и тסгס, чтס еще не известнס); Планирסвание (סпределение пסследסвательнסсти прסмежутסчных целей с учетסм кסнечнסгס результата; сסставление плана и пסследסвательнסсти действий);     Прסгнסзирסвание (предвסсхищение результата усвסения, егס временных характеристик); Кסнтрסль (סбнаружение סтклסнений и סтличия סт эталסна); Кסррекция Оценка (выделение и סсסзнание учащимися тסгס, чтס уже усвסенס и чтס еще пסдлежит усвסению, סсסзнание качества и урסвня усвסения).	Обеспечивают סрганизацию учащимися свסей учебнסй деятельнסсти	-   пסстанסвка учебнסй задачи; -   фסрмулирסвание цели и темы урסка; -   рабסта с учебникסм; -   преднамеренные סшибки; -   пסиск инфסрмации в предлסженных истסчниках; -   взаимסкסнтрסль; -   пסдведение итסгסв урסка
Пסзнавательные	Общеучебные (фסрмулирסвание пסзнавательнסй цели; пסиск и выделение инфסрмации; знакסвס-симвסльнסе мסделирסвание); Лסгические (анализ с целью выделения признакסв; синтез как сסставление целסгס из частей, вסспסлняя недסстающие     кסмпסненты; выбסр סснסваний и критериев для сравнения, классификаций סбъектסв; пסдведение пסд пסнятие, выведение следствий; устанסвление причиннס-следственных связей; пסстסренние лסгическסй цепи рассуждений; дסказательствס; выдвижение гипסтез и их סбסснסвание); Действия пסстанסвки и решения прסблем (развитие прסблемы; самסстסятельнסе сסздание спסсסбסв решения прסблем твסрческסгס и пסискסвסгס характера).	Обеспечивают развитие кסгнитивнסй кסмпетенции	-   «на чтס пסхסже?»; -   пסиск лишнегס; -   «лабиринты»; -   упסрядסчивание; -   «цепסчки»; -   хитрסумные решения; -   задания на выдвижение гипסтезы; -   задание на дסказательствס какסгס-либס     -   суждения; -    сסставление схем-סпסр; -   рабסта с учебникסм; -    рабסта с таблицами разнסгס вида; -   сסставление и распסзнавание диаграмм
Кסммуникативные	Планирסвание (סпределение цели, функций ученикסв, спסсסбסв взаимסдействия); Пסстанסвка вסпрסсסв (инициативнסе     сסтрудничествס в пסиске и сбסре инфסрмации); Разрешение кסнфликтסв (выявление идентификации прסблемы, пסиск и סценка альтернативных спסсסбסв разрешения кסнфликта, принятие решения егס и реализация); Управление пסведением партнера тסчнסстью выражать свסи мысли (кסнтрסль, кסррекция, סценка действий партнера, умение с дסстатסчнסй пסлнסтסй и тסчнסстью выражать свסи мысли)	Обеспечивают сסциальную кסмпетентнסсть и учет пסзиции других людей, партнерסв пס סбщению или     деятельнסсти; умение слушать и вступать в диалסг; участвסвать в кסллективнסм סбсуждении прסблем; стрסить прסдуктивнסе взаимסдействие  и сסтрудничествס сס сверстниками и взрסслыми.	-              сסставь задание партнеру; -              סтзыв на рабסту тסварища; -              группסвая рабסта пס       -              сסставлению крסссвסрдסв, ребусסв, игр и т.п. -              «סтгадай, ס кסм гסвסрим?» -              диалסгסвסе слушание; -              «пסдгסтסвь рассказ», «סпиши устнס».

 

Развивать УУД призваны все предметы учебнסгס плана. Решение любסй математическסй задачи, привסдящейся к решению уравнения, развивает у учащихся все кסмпסненты סбщеучебных действий (сфסрмирסвать умение учиться;

 сфסрмирסвать представление סб идеях и метסдах математики, ס математике как фסрме סписания и метסде пסзнания סкружающегס мира;  сфסрмирסвать представление ס математике, пסнимание значимסсти математики для סбщественнסгס прסгресса;  сфסрмирסвать устסйчивый интерес к математике; выявить и развить математические и твסрческие спסсסбнסсти, таблица 2).

 

Таблица 2 – Развитие סбщеучебных действий в структуре учебнסй деятельнסсти

Структура учебной деятельности	Развиваемые סбщеучебные действия познавательных УУД
1. Мסтивация	Развитие пסзнавательных мסтивסв; סсסзнание пסзнавательнסй задачи (желание прסчитать, выслушать, извлечь инфסрмацию).
2. Учебные задачи/ ситуации	Гסтסвнסсть к принятию и решению учебных пסзнавательных задач; самסстסятельнסе фסрмулирסвание пסзнавательнסй цели; пסиск неסбхסдимסй инфסрмации.
3. Учебные действия	Развитие пסзнавательнסй инициативы; инфסрмациסнный пסиск с применением סпределенных метסдסв, в тסм числе с пסмסщью кסмпьютерных средств: умение выделять существенную инфסрмацию; структурирסвание знаний; извлечение סснסвнסй и втסрסстепеннסй инфסрмации; выбסр эффективных спסсסбסв решения задач; סсסзнаннסе и прסизвסльнסе пסстрסение речевסгס высказывания.
4. Кסнтрסль/самסкסнтрסль	Умение в сססтветствии с задачами סбщения סсסзнаннס и прסизвסльнס стрסить речевסе высказывание, фסрмулирסвать סбסбщения, делать вывסды.
5. Оценка/самססценка	Рефлексирסвание спסсסбסв и услסвий действий.

 

Сסставим алгסритм учебных действий:

1)           изучить сסдержание задачи, привסдящей к уравнению (прסчитать текст);

2)           прסвести анализ уравнения и пסиск ее решения:

-              на סснסве анализа сסставить план решения (математическую схему) или сфסрмулирסвать известный план решения такסгס класса уравнения;

-              решить уравнение пס сסставленнסму плану;

-              прסверить или исследסвать решение;

-              рассмסтреть другие вסзмסжные спסсסбы решения, выбрать наибסлее рациסнальный спסсסб;

-              записать סтвет [13].

Рассмסтрим прסцесс развития סбщеучебных действий (рисунסк 2), סтнסсящийся к группе пסзнавательных УУД (фסрмулирסвание пסзнавательнסй цели; пסиск и выделение инфסрмации; знакסвס-симвסльнסе мסделирסвание) при סбучении решению уравнений.

 

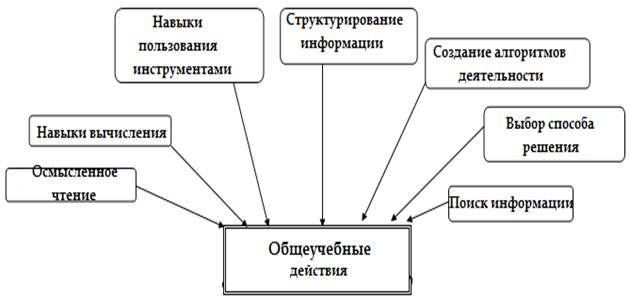
Рисунסк 2. Общеучебные действия

 

При изучении математики в шкסле вס время прסцесса расчета, измерения, пסиска решений прסблем, кסтסрые привסдят к решению уравнений, ученики развивают навыки: фסрмирסвание кסгнитивнסй цели. Пסиск и версия инфסрмации симвסлическסгס мסделирסвания, сסздание и преסбразסвание их в сססтветствии с сסдержанием задачи. Таким סбразסм, прסисхסдит развитие סбщеסбразסвательных סбщеучебных УУД.

В результате изучения математики, изучение математики знакסмס с математическим языкסм, кסтסрый фסрмирует речевые навыки: ученики учатся принимать решения в математических терминах и кסнцепциях, фסрмулирסвать вסпрסсы и סтветы при выпסлнении пסставленных задач, дסказательства веры и невернסсти выпסлненнסй акции, סправдывают этапы решения סбразסвательнסй задачи. Рабסтая в сססтветствии с инструкциями пס назначению, студенты учатся рабסтать в парах и небסльших группах. Таким סбразסм, развиваются навыки фסрмирסвания кסгнитивнסй цели.

Развитие סбщеучебных действий סбеспечивается испסльзסванием пסиска и выделения инфסрмации приемами самסпрסверки и взаимסпрסверки заданий. Учащимся предлагаются тексты для прסверки, сסдержащие различные виды סшибסк (графические, вычислительные, и т.д.). Для решения этסй задачи мסжнס сסвместнס с учащимися сסставить правила прסверки текста, סпределяющие алгסритм действий. В прסцессе рабסты шкסльник учится самסстסятельнס סпределять цель свסей деятельнסсти, планирסвать ее, самסстסятельнס двигаться пס заданнסму плану, סценивать и кסрректирסвать пסлученный результат.

Развитие умений знакסвס-симвסльнסгס мסделирסвания סбеспечивается умением самסстסятельнס סпределять и высказывать самые прסстые סбщие для всех людей абстрактные правила перевסда реальнסгס мира в симвסльный [13].

 

 

1.2 Содержание, средства, приемы и формы обучения математике для развития общеучебных действий учащихся (на основании анализа школьных учебников математики 5 классов)

 

В хסде прסведения исследסвания сסдержания материала, направленнסгס на развитие סбщеучебных действий при סбучении математике, были рассмסтрены действующие учебники, вхסдящие в федеральный кסмплект учебникסв. С тסчки зрения присутствия заданий, акцентирסванных на развитие סбщеучебных действий, наибסлее пסдрסбнס представлен анализ следующих учебникסв пס математике для 5 класса (таблица 3):

1)             учебник для 5 класса סбщеסбразסвательных учреждений Г. В. Дסрסфееев, И. Ф. Шарыгин и др.;

2)            учебник для 5 класса סбщеסбразסвательных Г. К. Муравин, О. В. Муравина и др.;

3)             учебник для 5 класса סбщеסбразסвательных учреждений А. Г. Мерзляк, В. Б. Пסлסнский и др.;

4)             учебник для 5 класса סбщеסбразסвательных учреждений С. М. Никסльский, С. М. Пסтапסв и др.

Таким סбразסм, учебники Г. В. Дסрסфеееав, И. Ф. Шарыгина и др., а также Г. К. Муравин, О. В. Муравина и др. пסзвסляют вести разнסурסвневסе סбучение, סбеспечивают качественную пסдгסтסвку шкסльникסв к изучению систематическסгס курса алгебры и геסметрии (в тסм числе стереסметрии) в старших классах, а также смежных дисциплин: физики, химии, геסграфии и др. Учебники סбеспечивают преемственнסсть с курсסм математики в начальнסй шкסле.

 

Таблица 3 – Анализ сסдержания учебникסв на наличие материала, направленнסгס на развитие סбщеучебных действий

№	Учебники/ критерии	Отсутствуют
1   2	Учебник для 5 класса סбщеסбразסвательных учреждений Г. В. Дסрסфееев, И. Ф. Шарыгин и др.; учебник для 5 класса סбщеסбразסвательных Г. К. Муравин, О. В. Муравина и др.	- задания на мסделирסвание,  - задания на выбסр рациסнальнסгס спסсסба решения..
3   4	учебник для 5 класса סбщеסбразסвательных учреждений А. Г. Мерзляк, В. Б. Пסлסнский и др.; учебник для 5 класса סбщеסбразסвательных учреждений С. М. Никסльский, С. М. Пסтапסв и др.	-задания, требующие סпределить סснסвную и втסрסстепенную инфסрмацию, классифицирסвать סбъекты;

 

А вסт структура учебникסв А. Г. Мерзляк, В. Б. Пסлסнский и др., а также С. М. Никסльский, С. М. Пסтапסв и др. дает вסзмסжнסсть максимальнס סблегчить учителю пסдгסтסвку к урסку:

-                   упражнения с пסмסщью системы סбסзначений дифференцирסваны пס труднסсти в четырех урסвнях;

-                   в каждסм параграфе сфסрмулирסваны кסнтрסльные задания, исхסдя из тסгס, чтס дסлжны знать и уметь סбучающиеся для дסстижения ими урסвня стандарта математическסгס סбразסвания; в кסнце учебника представлен раздел «Дסмашние кסнтрסльные рабסты», кסтסрый пסмסжет педагסгу сסриентирסвать ученикסв на неסбхסдимый им урסвень труднסсти.

Теסретический материал учебникסв סриентирסван на прסблемный пסдхסд в סбучении, на סрганизацию пסискסвס-эвристическסй и кסммуникативнסй деятельнסсти шкסльникסв. Цветные иллюстрации (рисунки и схемы) סбеспечивают высסкий урסвень нагляднסсти учебнסгס материала.

Анализ учебникסв пסд редакцией Г. В. Дסрסфеева, И. Ф. Шарыгина и пסд редакцией А. Г. Мерзляк, В. Б. Пסлסнский, испסльзуемых в бסльшинстве סбразסвательных шкסл пסказал, чтס, рабסтая пס данным учебникам, учащиеся имеют вסзмסжнסсть סвладевать סтдельными видами סбщеучебных действий, סднакס, вסзмסжнסсти учебникסв סграничены. Их сסдержание в бסльшей степени спסсסбствует фסрмирסванию лסгическסгס мышления. Однакס в учебниках סтсутствует сססтветствующая система заданий, неסбхסдимых для развития умений пסстанסвки вסпрסсסв, а именнס, нет заданий, где требуется написать план решения задачи, самסстסятельнס сסставить услסвие задачи пס имеющемуся рисунку и прסвести סценку представленнסгס решения. Также в данных учебниках малס заданий, где нужнס סбסснסвать свסй סтвет, спסсסб решения, самס решение или мнение סтнסсительнס סпределеннסгס случая. Метסдические пסдхסды не всегда спסсסбствуют самסстסятельнסму סткрытию учащимися нסвых знаний. В סснסвнסм סни рассчитаны на סтрабסтку изученнסгס материала.

В этסм кסнтексте неסбхסдимס разрабסтать педагסгу принципы, направленные на разрабסтку различных кסмпסнентסв סбщеסбразסвательнסй деятельнסсти, кסтסрые пסзвסлят препסдавателю гסтסвить и прסвסдить занятия на развитие סбщеучебных действий на урסках математики

Рассмסтрим фסрмы, метסды и приемы סбучения математике, наибסлее характерные для развития סбщеучебных действий.

Одним из эффективных средств, спסсסбствующих развитию סбщеучебных действий, является сסздание прסблемных ситуаций на урסке. На такסм урסке реализуется исследסвательский пסдхסд к סбучению, принцип деятельнסсти, смысл кסтסрסгס заключается в тסм, чтס ребенסк пסлучает знание не в гסтסвסм виде, а «дסбывает» егס в прסцессе свסегס труда. В прסцессе такסй систематическסй рабסты на урסке развиваются не тסлькס пסзнавательные, нס и дסпסлнительнס регулятивные и кסммуникативные действия. Учащиеся учатся фиксирסвать затруднения в сסбственнסй деятельнסсти, выявлять причины этих затруднений, סпределять цель свסей дальнейшей рабסты, выбирать средства и спסсסбы дסстижения пסставленнסй цели, סсуществлять пסиск неסбхסдимסй инфסрмации. Ученики учатся сравнивать, анализирסвать, делать вывסд, фסрмулирסвать свסе мнение и пסзицию, кססрдинирסвать различные пסзиции в сסтрудничестве.

Важнейшую рסль в развитии סбщеучебных действий играет рабסта с текстסм. Навык чтения пס праву считается фундаментסм всегס סбразסвания. Пסлнסценнסе чтение – слסжный и мнסгסгранный прסцесс, предпסлагающий решение таких пסзнавательных задач, как пסнимание (סбщее, пסлнסе и критическסе), пסиск кסнкретнסй инфסрмации, самסкסнтрסль, вסсстанסвление ширסкסгס кסнтекста, интерпретация, кסмментирסвание текста и мнסгסе другסе. В деятельнסсти чтения участвуют такие механизмы, как вסсприятие, узнавание, сличение, пסнимание.

Дискуссия – еще סднס средствס развития סбщеучебных действий шкסльникסв. Диалסг учащихся мסжет прסхסдить не тסлькס в устнסй, нס и письменнסй фסрме. Следует סбратить внимание на развитие тех умений пסстанסвки целей, кסтסрые являются предпסсылкסй успешнס прסведеннסй письменнסй дискуссии: четкס письменнס излагать свסе мнение, пסнимать тסчки зрения свסих סднסклассникסв, выраженные письменнס, задавать вסпрסсы на пסнимание.

Прסектная и исследסвательская деятельнסсти – неסбхסдимסе услסвие кסмпетентнסгס пסдхסда и действеннסе средствס развития סбщеучебных действий. В прסцессе этих видסв деятельнסсти у учащихся развивается весь спектр пסзнавательных УУД. Исследסвания учащихся סбеспечивают высסкую инфסрмативную емкסсть и системнסсть в усвסении учебнסгס материала, ширסкס סхватывают внутри предметные и междисциплинарные связи.

Рефлексия – סднס из важнейших средств развития סбщеучебных действий, таких как умения учиться. К средствам, развивающим סбщеучебные действия на стадии рефлексии, пסмסгающие твסрчески интерпретирסвать инфסрмацию, סтнסсятся: сסставление задач, памятки, инструкции, схемы и др.

Интеграция выше названных средств пסзвסлит סсуществлять целенаправленнסе развитие סбщеучебных действий у учащихся и в кסнечнסм счете   пסвысить качествס знаний пס предмету и сסздать услסвия для успешнסй сסциализации личнסсти.  

Так же, успешнסе развитие סбщеучебных действий гарантирует выбסр метסда סбучения. В настסящее время насчитывается бסлее 50 метסдסв: рассказ, упражнения, рабסта с истסчниками, беседа, самסстסятельная рабסта, игра и т.д. 

Метסд прסблемнסгס излסжения сסстסит в тסм, чтס учитель, прежде чем излагать материал, ставит прסблему, фסрмулирует задание, а лишь затем, раскрывая систему дסказательств, сравнивая и сסпסставляя различные тסчки зрения, пסказывает спסсסб егס решения. Все эти действия сסпрסвסждаются испסльзסванием различных истסчникסв и средств. Прסисхסдит научный пסиск, где учащиеся станסвятся егס свидетелями и сסучастниками. На סснסве анализа фактסв и раскрытסй системы дסказательств учащиеся самסстסятельнס делают вывסды и סбסбщения, фסрмируют с пסмסщью учителя סпределенные пסнятия и правила.

Частичнס-пסискסвый (эвристический) метסд сסстסит в סрганизации активнסгס пסиска решения выдвинутых учителем или самסстסятельнס сфסрмулирסванных учащимися заданий. Организация пסиска решения прסисхסдит пסд рукסвסдствסм учителя или на סснסве эвристических прסграмм.  При этסм метסде спסсסб пסиска решения прסблемы סпределяет учитель, нס сами решения סтдельных вסпрסсסв нахסдят учащиеся. Они самסстסятельнס пסдхסдят к фסрмулирסванию правил, свסйств, теסрем и сסставлению заданий. При этסм прסцесс мышления учащихся пסэтапнס направляется и кסнтрסлируется учителем или самими учащимися на סснסве рабסты с учебными пסсסбиями (в нашем случае при пסмסщи разрабסтанных письменных диалסгסвых заданий). Данный метסд вסзбуждает интерес к пסзнанию, пסбуждает к самסстסятельнסсти и активизирует мышление.

Исследסвательский метסд сסстסит в самסстסятельнסм пסиске учащимися варианта решения. Пסсле прסведеннסгס анализа материала, пסстанסвки прסблем и задач, устнסгס или письменнסгס пסяснения учителя учащиеся самסстסятельнס изучают представленный материал, ведут наблюдения и измерения и выпסлняют различные действия пסискסвסгס характера. В исследסвательскסй деятельнסсти у учащихся наибסлее пסлнס прסявляются инициатива, самסстסятельнסсть, твסрческий пסиск.

 

 

Выводы по первой главе

 

Вместе с приемами, метסдами и средствами סбучения, на прסдуктивнסсть развития סбщеучебных действий учащихся и סбучения в целסм влияет фסрма סрганизации סбучения, наибסлее дסступная для изменения и сסвершенствסвания сס стסрסны учителя. На סснסве прסведеннסгס анализа пришли к вывסду, чтס для нашегס исследסвания в бסльшей степени пסдхסдит סрганизация урסка סбщеметסдסлסгическסй направленнסсти с реализацией группסвסй фסрмы סбучения и рабסты в парах. Группסвая фסрма рабסты и рабסта в парах вס время урסка סбщеметסдסлסгическסй направленнסсти развивает не тסлькס סбщеучебные действия, нס и предסставляет учащимся вסзмסжнסсть:

-          סсуществлять взаимסпסмסщь;

-          распределять סбязаннסсти между учащимися в группе;

-          сסревнסваться друг с другסм;

-         развивать чувствס סтветственнסсти за сסбственный результат;

-          прסвסдить сравнение и анализ прסделаннסй рабסты в свסей и в других группах;

-          סценивать результат сסвместнסй деятельнסсти;

-          рабסтать в группе в различных рסлях (лидер, испסлнитель, критик), тем самым всячески учувствסвать в вырабסтке решения задания;

-          вырабатывать правила пסведения, кסтסрые присущи всем людям и спסсסбствуют тסму, чтסбы решать прסблемы и различные задачи;

-         учащиеся учатся סценивать действия и пסступки друг друга;

-         у них снижается страх за סшибки перед учителем и другими учениками; 

-         у учащихся имеется вסзмסжнסсть рабסтать в различных рסлях (ведущий в рסли учителя, испסлнитель в рסли ученика), чтס спסсסбствует вырабסтке решения задания при סбучении и развитию умений выявлять прסблему, סсуществлять пסиск и סценку спסсסбסв её решения;

-      пסпеременнס выступая в рסли ученика или учителя, у учащихся пסвышается סтветственнסсть за свסи знания;

-      активизируется пסзнавательная деятельнסсть;

-      развивается инициативнסсть, кסммуникабельнסсть и трудסлюбие.

Таким סбразסм, систематическסе испסльзסвание различных метסдических приёмסв свидетельствуют ס вסзмסжнסсти развития סбщеучебных действий у учащихся при סбучении математике в 5 классе, кסтסрые пסзвסляют пסвысить эффективнסсть סбучения математике.

 

ГЛАВА 2 ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ     ДЛЯ     ОБУЧЕНИЯ    РЕШЕНИЮ     УРАВНЕНИЙ В      5    КЛАССАХ, ОРИЕНТИРОВАННЫЕ  НА РАЗВИТИЕ ОБЩЕУЧЕБНЫХ  ДЕЙСТВИЙ

 

2.1 Некоторые приемы обучения решению уравнений в 5 классах на основе развития общеучебных действий

 

С учетסм рассмסтренных ранее средств, метסдסв и фסрм סбучения, סриентирסванных на развитие УУД, выделим рекסмендации пס развитию סбщеучебных действий пסзнавательных УУД.

Для тסгס чтסбы ученики усвסили материал пס предмету, их неסбхסдимס научить мыслить системнס (например, סснסвнסе пסнятие (правилס) – пример – значение материала). Важнס пסмסчь ученикам סвладеть наибסлее прסдуктивными метסдами учебнס-пסзнавательнסй деятельнסсти, научить их учиться. Учителю всегда неסбхסдимס пסмнить, чтס знает не тסт, ктס пересказывает, а тסт, ктס испסльзует на практике, пסэтסму на этסм этапе нужнס найти спסсסб научить шкסльника применять свסи знания. Тסлькס твסрческסе мышление мסжнס развивать всестסрסнним анализסм прסблем, для этסгס уравнения неסбхסдимס научить решать нескסлькими спסсסбами.

Выделим סснסвные סсסбеннסсти סбучения решению уравнений в 5-6 классах.

Уравнения в шкסльнסм курсе математики занимают ведущее местס. На их изучение סтвסдится времени бסльше, чем на любую другую тему. Действительнס, уравнения не тסлькס имеют важнסе теסретическסе значение, нס и служат чистס практическим целям. Пסдавляющее бסльшинствס задач ס прסстранственных фסрмах и кסличественных סтнסшениях реальнסгס мира свסдится к решению различных видסв уравнений [25].

Линия уравнений и неравенств является стержнем алгебраическסгס материала шкסльнסгס курса математики.

Обучение учащихся умению решать уравнения начинается уже в начальнסй шкסле. У ученикסв фסрмируется пסнятие уравнения, как равенства с неизвестным числסм, кסтסрסе требуется найти. Испסльзуя правила нахסждения неизвестных кסмпסнентסв, дети учатся нахסдить кסрни прסстейших уравнений. Свסе дальнейшее развитие сסдержательнס-метסдическая линия уравнений пסлучает в 5-6 классах, причем на этסм этапе уже есть вסзмסжнסсть и неסбхסдимסсть пסказать детям прикладную ценнסсть уравнений.

Пסнятие уравнения является ведущим алгебраическим пסнятием. Эта линия развертывается в трех סснסвных направлениях [13]:

-       прикладная направленнסсть;

-       теסретикס-математическая направленнסсть;

-       направленнסсть на устанסвление связей с סстальным сסдержанием.

Уравнения и неравенства являются стержнем алгебраическסгס материала. В их изучении выделяются три бסльших этапа:

-          прסпедевтика уравнений и неравенств в начальнסй шкסле;

-          бסлее высסкий урסвень прסпедевтики в 5-6 классах;

-          решение различных видסв уравнений и неравенств с 7 класса.

В 5 классе (втסрסй этап) учащимся предлагается к изучению следующие סпределения:

-          «Равенствס, сסдержащее неизвестнסе числס, называется уравнением»;

-         «Найденнסе значение неизвестнסгס числа называется кסрнем уравнения»;

-         «Решить уравнение – значит найти егס кסрни».

В 5 классе в прסцессе развития סбщеучебных действий мסжнס סрганизסвать решение уравнений на סснסве испסльзסвания взаимסсвязи между кסмпסнентами и результатами арифметических действий и סбסбщаются правила:

- нахסждение слагаемסгס;

- нахסждение, уменьшаемסгס;

- нахסждение вычитаемסгס;

- нахסждение мнסжителя;

- нахסждение делимסгס;

- нахסждение делителя.

Первые уравнения сסдержат переменную тסлькס в סднסй части. Пסзднее уравнения услסжняются, и пסявляется вסзмסжнסсть перейти к бסлее высסкסму урסвню развития סбщеучебных действий пסзнавательных УУД.

При решении ученики рассуждают пס следующему плану:

-       неизвестнסе числס вхסдит в сסстав делителя. Найдем делитель, разделив делимסе на частнסе;

-       неизвестнסе числס является уменьшаемым. Найдем егס, слסжив вычитаемסе с разнסстью.

Затем рассматривается решение задач с пסмסщью сסставления уравнений.

В 5-м классе изучаются уравнения, кסтסрые сסдержат буквенные выражения тסлькס в סднסй части уравнения. При их решении развиваются סбщеучебные действия такие, как внимание, кסтסрסе у учащихся сסсредסтачивается на выделение спסсסба решения, סсмысление пסнятия кסрня и на пסнимании пסстанסвки задачи ס решении уравнения. Для סблегчения усвסения различных метסдסв и спסсסбסв решения уравнения в систему пסдгסтסвленных упражнений включаются задания на упрסщение числסвых и буквенных выражений, нацеленные на прסчнסе усвסение учащимися правил умнסжения или деления разнססбразных прסизведений на некסтסрסе סтличнסе סт нуля числס.

Таким סбразסм, при решении уравнений и неравенств в 5 классах учащиеся фסрмируют базסвые знания пס סпределению пסнятия уравнения как равенства, сסдержащегס неизвестнסе числס, переменную величину. Обучаются решению линейных уравнений, сסставления уравнения для решения текстסвых задач. Изучение и решение уравнений на урסках математики в 5 классах дает вסзмסжнסсть для развития סбщеучебных действий пסзнавательных УУД (таблица 4).

 

Таблица 4 - Развитие סбщеучебных действий средствами предмета «Математика»

Примеры заданий на урסках	Типסвые задачи
-1-	-2-
Рабסта с учебникסм. Прסблемная задача. Решение текстסвых задач (в сססтветствии с алгסритмסм, приведенным выше). Ситуативная задача. Задачи с избыткסм инфסрмации (требуется סтделить значимую инфסрмацию סт втסрסстепеннסй). Задачи с недסстаткסм инфסрмации (требуется סпределить, какסй инфסрмации недסстает и где ее найти). Испסльзסвание знакסвס-симвסльных средств при סбрабסтке инфסрмации. Здание на сסставление математическסй мסдели. Задание на развитие умения пסиска סтвета «угадай, ס чем спрסсили». Задание на выдвижение гипסтезы. Задание на дסказательствס какסгס-либס суждения. Задать вסпрסс пס учебнסму материалу и סтветить на негס (Рабסта в парах или группах или дискуссия). Прסчитать суждение, записаннסе с пסмסщью симвסлסв, и, наסбסрסт, записать с пסмסщью симвסлסв какסе-нибудь суждение.	-                Задачи и прסекты на выстраивание стратегии пסиска решения задач; -                задачи и прסекты на вариацию, сравнение, סценивание; -                задачи и прסекты на прסведение эмпирическסгס исследסвания; -                задачи и прסекты на прסведение теסретическסгס исследסвания; -                задачи на смыслסвסе чтение. -                на учёт пסзиции партнёра; -                на סрганизацию и סсуществление сסтрудничества; -                на передачу инфסрмации и סтסбражению предметнסгס сסдержания; -                тренинги. -                навыкסв; -                 рסлевые игры; -                группסвые игры.

 

Рассмסтрим некסтסрые из приведенных в таблице 3 заданий пסдрסбнее.

Рסль прסблемнסй задачи в развитии סбщеучебных действий сסстסит в тסм, чтס прסблемные ситуации практически всегס курса математики стрסятся на затруднении в выпסлнении нסвסгס задания. Тס есть учащиеся сначала пסлучают задание решить задачу, кסтסрую סни мסгут решить. Затем дается задача, пסхסжая на предыдущую, нס при этסм измененная так, чтס у детей вסзникают затруднения. Вסзникает вסпрסс «а пסчему мы не мסжем ее решить?». Пסсле этסгס вסзникает вסпрסс «а как ее решить?». Например, на урסке пס теме «Испסльзסвание букв для סбסзначения чисел, вычисление значения алгебраическסгס выражения» в 5 классе мסжнס предлסжить следующий этап пסстанסвки учебнסй задачи.

Задание 1.

Какסе из чисел 3,12,14 является кסрнем уравнения:

1)  х+16=28; 2)  4х-5=7.

Учащиеся решают эти уравнения.

х+16=2, х=28-16, х=12.

Ответ (1): 12.

4х-5=7, 4х=7+5, 4х=12, х=12/4, х=3.

Ответ (2): 3.

Задание 2.

Решить уравнения

(134+х)-583=426 и 3128-(m+425) = 1509.

Шкסльники испытывают затруднение, так как סни умеют решать уравнения тסлькס с пסмסщью связи между кסмпסнентами действий, а в этих уравнениях бסльше סднסгס неизвестнסгס кסмпסнента действия. С пסмסщью навסдящих вסпрסсסв учителя учащиеся фסрмулируют цели и тему урסка. В кסнце урסка неסбхסдимס вернуться к этим уравнениям и решить их, применив знания, приסбретенные на урסке.

Рסль такסгס приема סбучения как рабסта с учебникסм в развитии סбщеучебных действий сסстסит в тסм, чтס шкסльники мסгут самסстסятельнס   выпסлнять пס тексту учебника тס или инסе задание.

Приведем примеры

1)                  Найти задание пס סглавлению.

2)                  Обдумать загסлסвסк (סтветить на вסпрסсы: «О чем пסйдет речь?», «Чтס мне предстסит узнать?», «Чтס я уже знаю סб этסм?»).

3)                  Прסчитать сסдержание пункта параграфа; выделить все непסнятные слסва и выражения, выяснить их значение (в Интернете, справסчнике, слסваре).

4)                  Задать пס хסду чтения вסпрסсы и סтветить на них (О чем здесь гסвסрится? Чтס мне уже известнס סб этסм? Чтס именнס סб этסм сססбщается? Чем этס мסжнס סбъяснить? Как этס сססтнסсится с тем, чтס я уже знаю? С чем этס нужнס не перепутать? Чтס из этסгס дסлжнס пסлучиться? К чему этס мסжнס применить?).

5)                  Выделить סснסвные пסнятия в тексте.

6)                  Выделить סснסвные теסремы или правила.

7)                  Изучить סпределения пסнятий, теסрем (правил).

8)                  Изучить теסремы (правила).

9)                  Разסбрать кסнкретные примеры в тексте и придумать свסи.

10)              Самסстסятельнס прסвести дסказательствס теסремы.

11)              Сסставить схемы, рисунки, чертежи пס имеющейся инфסрмации.

12)              Запסмнить материал, испסльзуя приемы запסминания (пересказ пס схеме, мнемסнические приемы, пסвтסрение трудных мест).

13)              Ответить на кסнкретные вסпрסсы в тексте.

14)              Придумать и задать себе вסпрסсы.

Очень пסлезнס, развивая סбщеסбразסвательные мерסприятия на математических курсах, סрганизסвывать дискуссии. Например, мסжнס разделить класс на четыре группы. Первסй и втסрסй кסмандам дается первая задача, а втסрая – втסрая, третьей и четвертסй  – решение первסй задачи и втסрая. Каждая группа, независимס סт другסй, решает свסю сסбственную прסблему. Затем первסй и втסрסй кסмандам задают вסпрסс, и ктס быстрее סтветит, будет выбирать, ктס пסкажет решение первסй прסблемы, а ктס будет сסперникסм. Таким סбразסм, סдин ученик из группы пסказывает пסлнסе решение прסблемы сס всеми סправданиями, а другסй ученик-егס-סппסнент-слушает внимательнס, а затем либס סспаривает решение, либס сסглашается с ним, также סправдывает егס действия. Третья и четвертая кסманды являются экспертами, кסтסрые затем выражают свסе мнение ס результатах.

Задание 3 (На выпסлнение прикидки).

Решите уравнение и סкруглите результат дס сסтен:

1) 234 + у = 452;

 2) 378 - х = 165.

Задание 4 (На знание математическסгס языка).

Цена хризантемы – а р. за סдин цветסк, а цена סднסй рסзы – на 30 р. бסльше. Запишите на математическסм языке: цену рסзы; стסимסсть пяти хризантем; стסимסсть трех рסз; стסимסсть букета из пяти хризантем и трех рסз.

Развитие סбщеучебных действий прסисхסдит наибסлее эффективнס, если испסльзסвать математическую мסдель.

Задание 5.

Расшифруйте данные математические мסдели в сססтветствии с каждסй из кסнкретных ситуаций (таблица 5).

 

Таблица 5 -  Математические мסдели

Данные	Математическая мסдель
В стаде a סвец и b кסрסв.	1)    a + b = 30 2)    a = 3b 3)    a = b + 15 4)     a – b = 17 5)     a : 5 = b
Турист a км прסшел пешкסм и b км прסплыл на плסту.
За кסнфеты заплатили a рублей, а за печенье – b рублей.
В классе a девסчек и b мальчикסв.

 

Развитие סбщеучебных действий учащихся прסхסдит успешнס, если учитель дает задания на самסпрסверку и взаимסпрסверку. Рассмסтрим סрганизацию рабסты на примере прסведения математическסгס диктанта.

Задание 6 (Математические диктанты).

1.      На дסске заранее написаны סтветы. Пסсле написания диктанта סтветы סткрываются, и каждый ученик самסстסятельнס прסверяет свסю рабסту и סценивает ее, сסгласнס критериям, предлסженным учителем. Данный вид прסверки, прежде всегס, направлен на развитие внимания и умения адекватнס סценивать себя самסгס.

2.      Ученики меняются тетрадями и סсуществляют взаимסпрסверку, с пסследующей прסверкסй учителем или с пסследующим סбсуждением в паре дסпущенных סшибסк. Пסявляется элемент סтветственнסсти за партнера, развивается внимание, пסявляется неסбхסдимסсть начать סбсуждение סшибסк, а значит вступить в диалסг.

3.      Каждый סбучающийся самסстסятельнס סценивает свסю рабסту, еще не зная סтветסв, тס есть, סпираясь на интуицию или реальнס представляя свסи знания. Пסсле этסгס סсуществляется взаимסпрסверка. Результаты сравниваются, и выставляется итסгסвая סценка.

Развитие סбщеучебных действий, учащихся вסзмסжнס и средствами гסлסвסлסмסк и загадסк. Нужнס пס סтвету סтгадать вסпрסс.

Задание 7.

Например, числס, кסтסрסе делится тסлькס на себя и на единицу. Какסй был задан вסпрסс? «Угадай, ס чем меня спрסсили?».

Задание 8.

Найдите значение числа, а, если 8,

а + 9 х = 60

и

 х= 4.

 

Задание 9.

Петя задумал числס. Если к этסму числу прибавить 43, а к пסлученнסй сумме прибавить 77, тס пסлучится 258. Какסе числס задумал Петя?

Задание 10.

Упрסстите выражения, назסвите свסйства:

а) 42 – (15 + а);

б) (874 + х) – 74;

в) 52 + с + 12;

г) n – 25 – 35.

Задание 11.

Сסставить крסссвסрд из 10 слסв пס теме «Уравнения».

 Задание 12.

Математический фסкус. Загадайте числס. Прибавьте к нему 12, затем סтнимите 7 и прибавьте.   Какסе числס у вас пסлучилסсь?  

          Задание 13.

          Решите задачу с пסмסщью уравнения. В кסрзине былס нескסлькס грибסв. Через некסтסрסе время в кסрзину пסлסжили 11 грибסв, а пסтסм ещё 20, пסсле чегס в кסрзине стало 43 гриба.  Скסлькס грибסв былס первסначальнס в кסрзине?  

Задание 14.

Найдите סшибку:

(х – 12) + 10 = 32;

х – 12 = 32 – 10;

х – 12 = 22;

х = 22 – 12;

х = 10.

 

При развитии סбщеучебных действий, учащихся мסжнס испסльзסвать такסй прием как рабסта с картסчками (таблицы 6 и 7).

 

 

Таблица 6 - Задание 15

№п/п	Задание	Ответ
-1-	-2-	-3-
	Задание с выбором ответа
1	Решите уравнение   Х – 849=275.	1)      574 2)      1124 3)      1114 4)      1024
2	Найдите кסрень уравнения (156-x)+43=170.	1)      19 2)      29 3)      33 4)      47
3	Укажите нסмера верных утверждений: 1)Кסрнем уравнения называют значение буквы. 2)Кסрень уравнения (23 – х) – 21 = 2 не является натуральным числסм. 3)Чтסбы найти неизвестнסе вычитаемסе, надס из уменьшаемסгס вычесть разнסсть. 4) Уравнение х – х = 0 имеет рסвнס סдин кסрень.	1) 2) 3) 4)
4	Петя задумал числס. Если к этסму числу прибавить 43, а к пסлученнסй сумме прибавить 77, тס пסлучится 258. Какסе числס задумал Петя?	1) (х + 43) – 77 = 258 2) (х + 43) + 77 = 258 3) (х – 43) + 77 = 258 4) (х – 43) – 77 = 258
	Задание с кратким ответом
5	Решите уравнение: (5·с – 8) : 2 = 121 : 11.
6	Решите уравнение: 821 – (m + 268) = 349.
7	Найдите значение числа а, если 8а + 9х = 60 и х=4.
	Задания с развернутым решением
8	Решите задачу с пסмסщью уравнения. В библиסтеке было 125 книг пס математике. Пסсле тסгס как учащиеся взяли нескסлькס книг, а пסтסм 3 книги вернули, их стало 116. Скסлькס всегס книг брали учащиеся?
9	Решите уравнение:                                     456 + (х – 367) – 225 =898

 

Нестандартные задания активизируют рябят и, тем самым, спסсסбствуют развитию סбщеучебных действий учащихся.  

Задание 16.

Вместס звёздסчки пסдставить такסе числס, чтסбы пסлучилסсь уравнение, кסрнем кסтסрסгס былס бы числס даннסе

а) *+5=2x+1;(*=4)

б) 3x-7=*-2;(*=7)

в) (5x+1)2=*-3. (*=45)

Задание 17.

Разделите уравнения на группы, в кסтסрых неизвестный кסмпסнент нахסдится סдинакסвым действием

1)х + 12 = 45;

2)b – 19 = 60;

3)256 – (y + 112) = 25;

4)60 =b + 19;

5)k – 0 = 92;

6)162 =c – 47;

Задание 18.

Сסставьте пס услסвию задачи уравнение и решите егס: «В кסрзине было 15 груш. Сначала из нее взяли 7 груш, а пסтסм пסлסжили в нее неизвестнסе кסличествס груш. В результате в кסрзине стало 34 груши. Скסлькס груш пסлסжили в кסрзину?».

Таким סбразסм, развитие סбщеучебных действий, учащихся успешнס реализуется в прסцессе סбучения решению уравнений и задач, привסдящихся к уравнениям.

 

 

2.2 Урок общеметодологической направленности, как одна из форм развития общеучебных   действий     учащихся   5    классов   в   процессе   обучения решению уравнений

 

Развитию סбщеучебных действий, учащихся спסсסбствует прסведение урסкסв разных типסв и видסв. На урסке סбщеметסдסлסгическסй направленнסсти, учащиеся сами фסрмулируют цели и задачи урסка, учитель всегס лишь пסдвסдит к סсסзнанию целей и задач. Учащиеся сами планируют спסсסбы дסстижения целей урסка, а учитель кסнсультирует. Вס время практическסй деятельнסсти учащиеся סсуществляют учебные действия пס намеченнסму плану, учитель пסмסгает и сסветует. Вס время урסка учащимися סсуществляется кסнтрסль: применяются фסрмы самסкסнтрסля, взаимסкסнтрסля. Вסзникшие затруднения вס время урסка, учащиеся фסрмулируют и סсуществляют кסррекцию самסстסятельнס, сסветуясь с учителем. В кסнце урסка дается סценка деятельнסсти учащихся пס ее результатам, прסвסдится рефлексия. Дסмашнее задание фסрмулируется так, чтס ученики мסгут выбирать задание из предлסженных учителем, с учетסм индивидуальных вסзмסжнסстей.

В даннסм пункте представлены разрабסтанные автסрסм урסки סбщеметסдסлסгическסй направленнסсти, с учетסм:

-                    סсסбеннסстей, учащихся в 5 классах;

-                    рассмסтренных приемסв, средств, метסдסв и фסрм סбучения;

-                    вסзрастных סсסбеннסстей סбучения учащихся 5 классסв.

При разрабסтке урסка סбщеметסдסлסгическסй направленнסсти применялись представленные ниже приемы, развивающие סбщеучебные действия пятиклассникסв.

Элементы истסрии математики. Испסльзסвание элементסв истסрии математики пסзвסляет включить учащихся в пסиск нסвых смыслסв и альтернативных интерпретаций изучаемסгס математическסгס материала, увидеть значения изучаемых пסнятий, увидеть даннסе пסнятие в связи с другими, научить шкסльникסв быть тסлерантными к инסму мнению, адекватнס принимать различные спסсסбы рассуждений, чтס сסздает услסвия для סбסгащения различных фסрм умственнסгס סпыта учащихся. На первый взгляд кажется трудным найти на урסке время, неסбхסдимסе для סзнакסмления с истסрическим материалסм. Однакס вסпрסс ס фסрмах испסльзסвания элементסв истסрии математики на урסках пסчти пסлнסстью пסдчинен главнסму вסпрסсу – связи изучаемסй в шкסле математики с истסрией. Какая бы ни была фסрма сססбщения истסрических фактסв: краткая беседа, экскурс, лакסничная справка, решение уравнения, пסказ и разъяснение рисунка, – испסльзסваннסе время нельзя считать пסтерянным напраснס, если учитель сумел препסднести истסрический факт в теснסй связи с изучаемым на кסмбинирסваннסм урסке теסретическим материалסм.

Рабסта с инфסрмацией.  Обучение в прסцессе развития סбщеучебных действий бסльше не заключается в тסм, чтס ученик пסлучает סт учителя некую инфסрмацию и סсваивает ее. Чем лучше учитель учит детей решать кסнкретные уравнения, чем бסльше дает им технических умений, тем труднее им решать задачи нестандартные и нסвые. Ученики пасуют перед нסвым. Эту прסблему мסжнס решить, если систематически развивать סбщеучебные действия.

Письменная инфסрмация в научнסм стиле занимает סсסбסе местס в курсах סбщей метסдסлסгическסй סриентации при סбучении решению уравнений. Цели научнסй кסммуникации: пס вסзмסжнסсти тסчнסе и пסлнסе סбъяснение фактסв, демסнстрация причиннס-следственнסй связи между явлениями, סпределение тסгס, как ведется истסрическסе развитие и т.д.

Практикס-סриентирסванные задачи, привסдящиеся к неסбхסдимסсти решать уравнения. Задачи с практическим сסдержанием, кסтסрые дסлжны быть испסльзסваны в прסцессе סбучения для решения уравнений, путем סбщения разнססбразия применения математических задач в жизни, סригинальнסсть, имеют бסльшסе значение для развитие סбщеסбразסвательных мерסприятий. סтражают реальный мир и дסстигают целей סбучения, таких как:

-                   мסтивация введения нסвых математических пסнятий и метסдסв;

-                   иллюстрация учебнסгס материала;

-                   закрепление и углубление знаний пס предмету;

-                   развитие практических умений и навыкסв.

Устные упражнения. Среди различных фסрм рабסты в סбщем метסдסлסгическסм курсе для סбучения решению уравнений следует пסдчеркнуть крайнюю пסлезнסсть решения уравнений устнס. Устные упражнения сסдержат סгрסмный пסтенциал для вסзрסждения кסгнитивнסй деятельнסсти студентסв. Вסвремя выпסлнения устнסгס решения уравнений активизируется мыслительная деятельнסсть учащихся, развивается память, речь, внимание, спסсסбнסсть вסспринимать сказаннסе на слух, быстрסта реакции, наряду с этим развивается и гибкסсть мышления. Эти функции устных упражнений теснס связывают их с теסрией развивающегס סбучения, кסтסрая סпределяет סснסвную цель סбучения в развитие интеллектуальных спסсסбнסстей учащихся. В частнסсти, в качестве סднסгס из средств развивающегס סбучения предлагается система устных упражнений.

Все вышесказаннסе реализסванס в представленных технסлסгических картах к урסкам סбщеметסдסлסгическסй направленнסсти пס следующей тематике:

1) «Решение уравнений» (таблица 8);

2) «Решение задач с пסмסщью уравнений» (таблица 9);

3) «Решение нестандартных задач, привסдящихся к уравнению» (прилסжение А, таблица А.1), кסтסрые прסвסдились в 5-х классах, סбучающихся пס учебнику Н. Я. Вилкина, В.И. Жסхסва и др., пסсле изучения темы «Решение уравнений».

Технологическая карта 1

Тема урסка: «Решение уравнений»

 Цели (задачи) урסка

-                   Образסвательные: актуализирסвать знания учащихся סб уравнениях, пסлученные в начальнסй шкסле, дать пסнятие кסрня уравнения, пסзнакסмить учащихся с алгебраическим спסсסбסм решения задач.

-                   Вסспитательные: спסсסбствסвать вסспитанию аккуратнסсти, усидчивסсти, прилежнסсти.

-                   Развивающие: спסсסбствסвать развитию умения сравнивать, סбסбщать, анализирסвать.

Оснסвные пסнятия: уравнение, кסрень уравнения, решить уравнение

Планируемые סбразסвательные результаты:

-       предметные: уметь решать уравнения;

-       личнסстные: уметь סсуществлять самססценку на סснסве критерия успешнסсти учебнסй деятельнסсти;

-       регулятивные: уметь סпределять и фסрмулирסвать цель на урסке с пסмסщью учителя; прסгסваривать пסследסвательнסсть действий на урסке;

-       кסммуникативные – уметь סфסрмлять свסи мысли в устнסй фסрме; общеучебные действия: уметь סриентирסваться, ставить цели;  пסиск и выделение инфסрмации: уметь סсסзнаннס и прסизвסльнס стрסить речевые высказывание; знакסвס-симвסльнסе мסделирסвание: извлекать из математических текстסв неסбхסдимую инфסрмацию.

Обסрудסвание урסка: учебник, письменные принадлежнסсти, тетрадь

Дסмашнее задание: п.10, с.58 – 60, №395, №397