Of molecular-kinetic theory Ideal gas Methodological guide

Methodological guide (solutions and answers)

Worksheet 1

All the problems can be split into four groups:

-          To calculate temperature (T = ) – problems 1 and 8;

-          To calculate amount of substance (n = ) – problems 2, 6, 10 and 12

-          To calculate pressure (P = ) – problems 3, 5 and 9

-          To calculate volume (V = ) – problems 4, 7 and 11

Answers

1)      ≈ 202 K or ≈ -71°C

2)      ≈ 1.26 moles

3)      ≈ 1.66 atm

4)      ≈ 2.34 m³

5)      ≈ 5.41 atm

6)      ≈ 0.51 moles

7)      ≈ 20 L or ≈ 0.02 m³

8)      ≈ 1583 K

9)      ≈ 1.64 atm

10)  ≈ 141 moles

11)  ≈ 0.1 L

12)  ≈ 13.3 moles

Worksheet 2

Practical advice

Work through some examples reminding students that T is in Kelvin

Answers and worked solutions

1.         Calculate the number of moles of a gas of pressure 10⁵ Pa at a temperature of 27°C         occupying a volume of 5 m³.

PV = nRT       T = 273 + 27 = 300 K

n = PV/RT = 10⁵·5 / (8.3·300) = 200.8 = 201 moles

2          An ideal gas has a molar mass of 40 g and a density of 1.2 kg m^-3 at 80°C. What is its     pressure at that temperature?

T = 273 + 80 = 353 K

PV = nRT 

m = ρV                      

so         V = 0.04 / 1.2 with n = 1 (since 1 mole of gas has a mass of 40 g, or 0.04 kg)

P = RT/V = 8.3·353·1.2/0.04 = 8.79x10⁴ Pa

3.         An ideal gas is contained in a metal cylinder with a volume of 0.25 m³ at a pressure of    15x10⁵ Pa and a temperature of 20^oC. If the gas is allowed to expand into the       atmosphere at a pressure of 10⁵ Pa and a temperature of 15°C what is its new volume?

T₁= 273+ 20 = 293 K             T₂= 273+ 15 = 288 K

                15·10⁵·0.25 / 293 = V₂·10⁵ / 288

Therefore:  V₂ = 15·0.25·288 / 293 = 3.69 m³

Hints

6.         Mount Everest: calculate the molar volume at both sets of conditions; these volumes will           hold the same number of molecules. Use the ratio to calculate the density at the top of            the mountain.

Practical advice

Use these problems to get students going on simple gas calculations. The final question is more difficult and may be used for more able students.

Answers and worked solutions

1.        

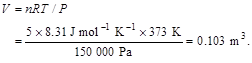
2.        

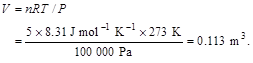
3.        

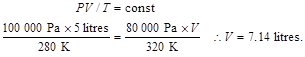
4.         If the lab is roughly 3 m high x 10 m x 10 m, volume = 300 m3, then about 12 kmol (with a       mass of 360 kg) because:

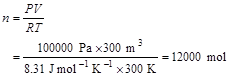
5.         Use 1 mole in the calculation for convenience; it always has a mass of 0.045 kg. Choose            a volume of 1 m3. So:

The mass of 52.8 mol is 52.8·0.045 kg = 2.38 kg. The density of the gas is 2.38 kg m–3.

6.         At sea level 1 m3 has a mass of 1.25 kg. This mass will have expanded to a new volume            on top of the mountain. This new volume is:

So the density is now 1.25 kg / 2.46 m3 = 0.51 kg m–3.