«Определение площади фигуры. Измерение площади»

 

введение 

Тема «Многоугольник. Площадь многоугольника» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. В школьном курсе математики изучается множество способов нахождения площадей плоских геометрических фигур, большинство из которых часто применяются не только в решении задач на уроках математики, но и в повседневной жизни. Материал о площади плоских фигур «разбросан» по всему курсу математики, в разных учебниках он преподносится по-разному. Поэтому необходимо обобщить и систематизировать этот материал и найти наиболее приемлемый способ его представления.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ

Площадь плоских фигур

Многие годы площадь считалась первичным понятием, не требующим определения. Основной задачей математиков являлось вычисление площади, при этом были известны основные свойства площади. В Древнем Египте использовались точные правила вычисления площади прямоугольников, прямоугольных треугольников и трапеций, площадь произвольного четырёхугольника определялась приближённо как произведение полусумм пар противоположных сторон. Применение такой приближённой формулы связано с тем, что участки, площадь которых надо было померить, были в основном близки к прямоугольным и погрешностьв таком случае оставалась небольшой. Историк математики А. П. Юшкевич предполагает, что египтяне могли и не знать, что пользуются приближённой формулой. В задаче 50 папируса Риндасодержится формула вычисления площади круга, которая считалась равной площади квадрата со стороной 8/9 диаметра круга. Такими же формулами пользовались и в Вавилоне, однако для площади круга приближение было менее точным. Кроме того, вавилоняне могли приближённо посчитать площади правильных пяти-, шести- и семиугольника со стороной равной единице. Вшестидесятиричной системе им соответствовали 1,40, 2,37,20 и 3,41, соответственно.

Основным приёмом вычисления площади при этом являлось построение квадрата, площадь которого равна площади заданной многоугольной фигуры, в частности в книге I «Начал» Евклида, которая посвящена планиметрии прямолинейных фигур, доказывается, что треугольник равновелик половине прямоугольника, имеющего с ним равные основания и высоту. Метод разложения, основанный на том, что две равносоставленные фигуры равновелики, позволял также вычислить площади параллелограммов и любых многоугольников.

Следующим шагом было вычисление площадей круга, кругового сектора, лунок и других фигур. Основу вычислений при этом составлял метод исчерпывания многоугольниками, с которого берёт начало теория пределов. Метод заключается в построении последовательности площадей, которые при постепенном нарастании «исчерпывают» требуемую площадь. Метод исчерпывания, получивший своё название только в XVII веке, основан на аксиоме непрерывности Евдокса — Архимеда и приписывается ЕвдоксуКнидскому, который с его помощью показал, что площади кругов относятся друг к другу как квадраты их диаметров. Метод описан в «Началах» Евклида: аксиома Евдокса сформулирована в книге V, а сам метод исчерпывания и основанные на нём отношения — в книге XII. Особого совершенства в применении метода достиг Архимед, который с его помощью посчитал площадь сегмента параболы и другие. Труд Архимеда «О спиралях» включает много утверждений, касающихся площадей различных витков спирали и их отношений. Архимеду принадлежит идея использования площадей или объёмов как вписанных, так и описанных фигур для определения требуемой площади или объёма.

Индийцы поначалу пользовались той же формулой для вычисления четырёхугольников, что египтяне и греки. Брахмагупта пользовался формулой для площади четырёхугольников, выраженной через его полупериметр., которая верна для вписанного в окружность четырёхугольника. Формулы вычисления площади обычно не доказывались, но демонстрировались с наглядными рисунками. Формула Брахмагупты представляет собой аналог формулы Герона для площади треугольника, которую тот привёл в своей «Метрике».

Развитие и обобщение метода исчерпывания произошло только в XVII веке. В 1604 году в работе «Три книги о центре тяжести тел» Валерио широко использует теорему, по которой разность между площадями вписанной и описанной фигур, составленных из параллелограммов можно сделать меньше любой данной площади. Настоящий прорыв был сделан Кеплером, которому для астрономических расчётов нужно было уметь вычислять площадь эллипса. Кеплер рассматривал площадь как «сумму линий» и, разлиновывая эллипс с шагом в один градус, показал, что  Кавальери, обосновывая подобный метод, названный «методом неделимых», сравнивал площади плоских фигур, используя сечение фигур параллельными прямыми. Применение первообразной для нахождения площади плоской фигуры является наиболее универсальным методом. С помощью первообразной доказываетсяпринцип Кавальери, по которому две плоские фигуры имеют равную площадь, если при пересечении каждой из них прямой, параллельной фиксированной, получаются отрезки одинаковой длины. Принцип был известен задолго до формирования интегрального исчисления.

Площадь поверхности

Вычислением площадей кривых поверхностей занимался Архимед, определив, в частности, площадь поверхности шара^[11]. В общем случае для определения площади поверхности нельзя пользоваться ни развёрткой (не подходит для сферы), ни приближением многогранными поверхностями, то есть аналогом метода исчерпывания. Последнее показал Шварц, построив для боковой последовательности цилиндра последовательности, которые приводят к разным результатам (так называемый сапог Шварца)^[1][17].

Общий приём вычисления площади поверхности на рубеже XIX—XX веков предложилМинковский, который для каждой поверхности строил «окутывающий слой» малой постоянной толщины, тогда площадь поверхности будет приближённо равна объёму этого слоя, делённому на его толщину. Предельный переход при толщине, стремящейся к нулю даёт точное значение площади. Однако, для площади по Минковскому не всегда выполняется свойство аддитивности. Обобщение данного определения приводит к понятию линии по Минковскому и другим^[18].

В Киевской Руси мер площади, как квадратных мер, судя по сохранившимся источникам, не было. Хотя, древнерусские зодчие и землемеры имели о них представление.

Меры площади нужны были для определения размеров земельных участков. Участки же не всегда были четко разграничены, соприкасались друг с другом, имели межевые знаки.

В древней Руси в целях податного обложения использовали чисто условные единицы, характеризовавшие рабочую силу или сельскохозяйственный инвентарь, а также меры, в основе которых лежали трудовые возможности. Отсюда такие наименования земледельных мер (единиц обложения), как «дом» (семья) или «дым», «рало», «соха», «обжа»и пр. Трудовой характер мер «соха» и «обжа» и их соотношение явствуют из сохранившегося ответа новгородцев на запрос Ивана III в 1478 г.: «Три обжи –соха, а обжа –1 человек на 1 лошади орет (пашет); а кто на 3 лошадях и сам третий орет, ино то соха».

Несмотря на неопределенность в геометрическом смысле, «посевные» меры оказались более удобными для земледельцев, кроме того, объективнее и точнее определялся размер податного обложения.

Для сенокосных угодий широко применяли «урожайные» меры –копны сена. Копны иногда использовали и в качестве мер посевных площадей.

Все «трудовые», «урожайные» и «посевные» меры заключали в себе элементы субъективизма и произвола, которые проявлялись непосредственно в практике использования этих мер.

Во время феодальной раздробленности Руси как меры площади применялись «дом»(дым), «соха»,«обжа». Но они отличались по количеству в зависимости от княжества. Отличия были и в наименованиях мер. В Новгороде, например, в качестве посевной меры применялась «коробья»(площадь, на которую высевали коробью ржи –меру объема).

Площади сенокосных участков оценивали копной (площадь луга, на которой можно накосить копну сена).Эти меры позволяли определить урожайность, а о форме и размерах земельных участков полного представления не давали.

В середине XIII века татары проводили в значительных масштабах описи земельных площадей. В основу описей в качестве единицы измерения было положено отдельное хозяйство («дом»или «дым»).

В памятниках древней письменности с конца XIV века упоминается геометрическая мера земельных площадей –десятина. Первоначально применяли «круглую»десятину –квадрат со стороной, равной десятой доле версты (50 сажен), откуда и происходит название «десятина». С середины XV века десятину стали употреблять для пахотных земель, а не только для сенокосных угодий. С этого момента можно говорить об использовании в землемерной практике действительно мер в метрологическом смысле слова.

Переход от четверти к десятине оказался затруднительным, т. к. в основе четверти лежало реальное засеваемое зерно, это было понятно всем, кроме того, в писцовых книгах было зафиксировано определение земельных площадей в четвертях.

 

ОПРЕДЕЛЕНИЕ ПЛОЩАДИ В ОСНОВАНИЯХ ГЕОМЕТРИИ

Площадь многоугольных фигур. Мы будем рассматривать только ограниченные фигуры, и слово «фигура» будет всегда обозначать плоскую  ограниченную фигуру, т. е. такую, которая содержится в  каком-нибудь круге.

Будем говорить, что фигура составлена из  нескольких фигур, если она служит их объединением и никакие две из них не имеют общих внутренних  точек. Под многоугольной фигурой будем всюду ниже понимать многоугольную площадку, рис. 18. Проще говоря, многоугольная фигура — это объединение конечного числа треугольников.

Площадью многоугольной фигуры называется  величина, обладающая следующими двумя свойствами:

1) равные фигуры имеют равные площади\

2) если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме  площадей этих фигур.

Первое свойство — инвариантность,  неизменяемость при перемещениях, второе—аддитивность; его достаточно требовать для того случая, когда фигура слагается из двух фигур.

Удобно ввести следующие обозначения.

Площадь будем обозначать  буквой S.

Вместо самой площади как  величины удобно рассматривать ее численное значение при данной  единице измерения и дать следующее определение.

«Численной площадью» —  численным значением площади фигуры F при данной «единичной» фигуре Е — называется число S(F), относимое  многоугольной фигуре, каждой — свое, так что выполнены  условия:

1) S(F)>0,

2) если F^F`, то S (F) = S (F'),

3) S(F1 + F2) = S(Fl) + S(F2),

4) S(Е)=l.

Последнее условие означает, что единичная  фигура— это та многоугольная фигура Е, которой  отнесено численное значение площади, равное единице.

В качестве такой фигуры берут «единичный квадрат», т. е. квадрат со стороной, равной выбранной единице длины. Но это совершенно не обязательно:  единичной фигурой может быть, в принципе, любая  многоугольная фигура.

По аддитивности S(F) = S(F1) + S(F2), и поэтому S(F)>S(F1).

Дальше мы будем говорить о площади, допуская, что под «площадью» можно разуметь как саму  величину, так и ее численное значение при какой-нибудь единице измерения, которую можно для дальнейшего выбрать раз навсегда. В большинстве случаев  удобнее иметь в виду именно численное значение, когда говорится о сложении и сравнении площадей (но не об их измерении: измеряется  величина, а ее численное  значение — это результат измерения).

То, что у каждой  многоугольной фигуры, в частности у  квадрата, есть определенная площадь, представляется, в общем, как  нечто само собой разумеющееся. Но можно задать следующий вопрос. Представим себе, что, разбив квадрат или другой  многоугольник на какие-то многоугольники, мы перемещаем их так, чтобы они не налегали друг на друга. Мы будем получать различные новые  фигуры. Не может ли при этом получиться такая фигура, которая уместится внутри первоначального  многоугольника или внутри одной из полученных из него новых фигур. Если бы это случилось, то мы имели бы две фигуры, у которых, с одной стороны, площади должны быть равны, так как они составлены из  попарно равных фигур. С другой стороны, у фигуры, умещающейся внутри другой, площадь меньше. То есть получалось бы противоречие. Выходило бы, что понятие о равенстве или неравенстве площадей и, стало быть, само понятие о площади оказались  лишенными смысла. Мы скажем: «не может быть, чтобы одна фигура уместилась внутри другой, ведь у них площадь одна и та же». Но именно об этом и стоит вопрос: имеет ли смысл понятие площади? Иначе говоря:  существует ли в самом деле такая величина, как площадь, у многоугольных фигур?

Можно поставить и другой вопрос. Площадь  прямоугольника определяют, покрывая его квадратами (рис. 20, а), и квадраты эти берутся такими, что стороны их параллельны сторонам прямоугольника.

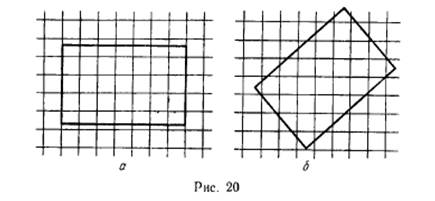
А что будет, если брать квадраты, повернутые  относительно прямоугольника или, что равносильно,  повернуть прямоугольник, как на рис. 20,6? Будет ли подсчет таких квадратов давать то же самое (в  пределе, когда квадраты уменьшаются)? Иначе говоря, будет ли (в пределе) площадь маленьких квадратов, укладывающихся на прямоугольнике, той же самой, с точностью до квадратов, которые пересекаются со сторонами прямоугольника?

Мы уверены, что результат будет тот же, потому что у фигуры есть определенная площадь, так что ее измерение должно давать всегда один и тот же  результат. Но именно об этом и идет речь: существует ли у фигуры определенная площадь, независимая от того, как мы ее измеряем?

Приведенные рассуждения показывают, что  существование площади, т. е. существование величины со свойствами 1, 2, вовсе не так очевидно, как кажется на первый взгляд. Существование ее нужно  доказать.

Доказательство может быть дано. Именно,  доказывается следующая теорема.

Теорема I. Каждая многоугольная фигура имеет определенную площадь.

Для численных значений это можно выразить так.

При заданной единичной фигуре Е каждой  многоугольной фигуре отвечает, и притом единственная, численная площадь со свойствами 1, 2, 3, 4.

Если фигура Е заменяется другой, то все  численные площади изменяются на один и тот же  множитель.

Ту же теорему можно высказать иначе.

Существует, и притом единственная, функция со свойствами 1—4, определенная на множестве  многоугольных фигур. Функции, соответствующие разным «единичным» фигурам», отличаются множителем.

То есть за площадь фигуры F принимается  величина, которая не больше площадей многоугольных фигур, содержащих F, и не меньше площадей  многоугольных фигур, содержащихся в F.

Однако площади фигур G и F могут отличаться так, что между ними будет целый интервал величин, и, стало быть, величина S(F) не будет единственной.

Площадь оказывается неопределенной. Она будет  определенной, если разность площадей S(G), S(H)  может быть сколь угодно малой.

Таким образом, мы приходим к окончательному определению, которое, как легко видеть,  воспроизводит в общем виде школьное определение площади круга.

Площадью фигуры F называется величина,  которая не больше площадей многоугольных фигур,  содержащих Т7, и не меньше площадей многоугольных фигур, содержащихся в Fy при условии, что разности этих площадей могут быть сколь угодно малыми.

Мы говорим тогда, что фигура F имеет  определенную площадь. Всякая многоугольная фигура F попадает под это определение, поскольку тогда сама F оказывается многоугольной фигурой, содержащей Fи содержащейся в F.

Оказывается, что так определенная площадь и для немногоугольных фигур обладает теми же  свойствами, какие определяют площадь многоугольных фигур, т. е. выполняется

Теорема II. Определенная только что площадь  обладает свойствами инвариантности и аддитивности:

1. Если фигура F имеет определенную площадь S(F), то всякая равная ей фигура F` тоже имеет  определенную площадь, и притом равную S(F).

2. Если фигура F составлена из фигур F1, F2 с  определенными площадями S(F1), S(F2), то она тоже имеет определенную площадь S(F) и S(F) = S(F1) + S(F2)

Выразим условие, при котором фигура имеет  определенную площадь, несколько иначе.

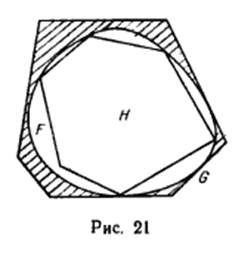
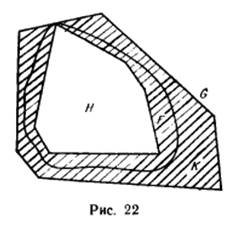
Если многоугольная фигура Н содержится в  фигуре F, то многоугольная фигура G, содержащая F9 получается прибавлением к Н некоторой 

многоугольной фигуры К—«разности» G — Н. Эта фигура,  очевидно, содержит границу фигуры F (рис. 21, 22). Ее площадь равна разности площадей фигур G и Н:

S(K) = S(G)-S(H).

Стало быть то, что площади фигур G и Н могут быть сколь угодно близки и тем самым фигура F имеет определенную площадь, равносильно тому, что и  площадь фигуры G — Н может быть сколь угодно малой. То есть граница данной фигуры F может быть заключена в многоугольную фигуру сколь угодно малой площади. И можно сформулировать: фигура имеет определенную площадь тогда и только тогда, когда ее границу можно заключить в многоугольную фигуру сколь угодно малой площади. Но если  фигура может быть заключена в многоугольную фигуру сколь угодно малой площади, то ее площадь равна нулю (как, например, равна нулю площадь отрезка).

Это позволяет выразить полученное условие  существования у фигуры определенной площади так.

Теорема 1. Фигура имеет определенную площадь тогда и только тогда, когда площадь ее границы равна нулю.

И можно пересказать теорему II:

Теорема II. Площадь фигур с определенной  площадью обладает теми же свойствами 1—4, как, в  частности, площадь многоугольных фигур.

Эта теорема будет доказана в следующих  параграфах. К определению площади можно подойти, исходя из способа ее измерения с помощью квадратных  сеток (рис. 23). Это обобщает тот прием, каким  находят площадь прямоугольника или измеряют площадь практически с помощью палетки. Коротко можно  сказать:

Площадь фигуры можно определить как величину, измеряемую площадью квадратов сетки,  содержащихся в фигуре и покрывающих фигуру, если у этих чисел есть общий предел.

Это определение одинаково для многоугольных и других фигур и равносильно данным выше. На его основе и будут дальше доказаны теоремы I, II.

Замечание 1. То условие, что фигура имеет  определенную площадь, если площадь ее границы равна нулю, мало наглядно и, что более существенно, само

использует понятие площади. Однако заменить его другим не удается, и можно указать только те или иные более частные условия, когда оно выполняется.

Следующее условие будет все же достаточно общим.

Назовем криволинейным отрезком такую фигуру— кривую, — которая в подходящих координатах  представляется уравнением y = f(x) с непрерывной 

функцией f, заданной на каком-либо замкнутом  промежутке. 

Теорема III. Всякая фигура, ограниченная  конечным числом криволинейных отрезков, имеет  определенную площадь; для таких фигур выполняется все то, что было сказано о площади многоугольных фигур.

Замечание 2. Приведем пример фигуры без  определенной площади. Представим себе прямоугольник, составленный из двух квадратов Р, Q с общей 

стороной. Пусть на одной стороне квадрата Р введена координата х. Представим себе также фигуру R,  состоящую из всех лежащих в этом квадрате отрезков, параллельных другой его стороне и имеющих концы в точках с рациональными значениями координаты х. Эти отрезки плотно «штрихуют» весь квадрат. 

Фигура F, составленная из квадрата Q и фигуры R,  содержится в прямоугольнике Р + Q, содержит  квадрат Q, но большей многоугольной фигуры не  содержит. Эта фигура F не имеет определенной площади.

В этом примере фигура F имеет часть R довольно необычного «патологического» строения. Но можно привести примеры областей, которые не имеют  определенной площади. Эти примеры строятся не так  просто, и мы их здесь приводить не будем. Полезно, однако, знать, что даже не всякая область имеет определенную площадь в смысле принятого выше определения.

Это можно понять практически. Представим себе земельный участок, ограниченный с одной стороны оврагом с сильно изрезанным краем. Для владельца участка зигзаги края неудобны, и площадь участка он будет измерять без них. Но землеустроитель  может настаивать на том, чтобы учитывать и площадь «зигзагов». Таким образом, практически оказывается, что площадь можно оценивать по-разному. 

Математическая идеализация и приводит к областям, не имеющим определенной площади из-за особенностей границы.

Замечание 3. Подобно тому как для  многоугольных фигур площадь есть функция со свойствами 1—4, так можно сказать, что, вообще, площадь других 

фигур— это функция с теми же свойствами. Однако для того, чтобы функция была определена, нужно  указать область ее задания, в нашем  случае—множество тех фигур, для которых она определена, но  характеризуется другими свойствами.

 

Определение площади измерением

Представим себе, что плоскость разбита прямыми на единичные квадраты подобно клетчатой бумаге.

Эти квадраты в свою очередь разбиты на меньшие равные квадраты, те на еще меньшие, и т. д. Так мы представляем себе последовательность все более уменьшающихся квадратных сеток, покрывающих плоскость. Эти сетки мы перенумеруем: первая,  состоящая из единичных квадратов, вторая, третья и т. д.

Единичному квадрату и, соответственно, всем квадратам первой сетки припишем площадь, равную единице:

S(E1)=1.

Если в n-й сетке единичный квадрат разделен на Nn квадратов, то каждому квадрату n-й сетки  приписываем площадь.

Фигуре, составленной из квадратов сетки,  приписывается площадь, равная сумме их площадей. (Мы говорим здесь «площадь» для краткости, хотя имеем

в виду численную площадь; строго говоря, пока речь идет о числах, приписываемых фигурам в качестве их численной площади.)

Пусть теперь F— какая-либо фигура. Сопоставим ей две фигуры из квадратов п-и сетки: Fit Fen (i, е — первые буквы слов interior — внутренний, exterior —

внешний). Фигура Fn состоит из всех квадратов п-й сетки, внутренности которых содержатся в F (рис.23).

Площадью (численной площадью) фигуры  называется общее значение ее внешней и внутренней  площади, когда они равны.

Вначале фигурам, составленным из квадратов  какой-либо сетки, была приписана площадь — сумма площадей этих квадратов. Нужно убедиться, что это согласуется с данным общим определением площади.

Пусть фигура F состоит из квадратов m-й сетки; тем самым F = Flm = Fem и при всех п>т также F = Fln = Fen. Поэтому при всех п> т площадь, первоначально приписанная фигуре F, будет S(F)^S(Fin) = S(K).

В пределе получим S(F) = Si(F)-=Se(Fh т. е. S(F) является общим значением внутренней и внешней площади. Тем самым S(F) является  площадью фигуры F в смысле данного общего  определения.

Итак, мы сопоставили некоторым фигурам числа S(F) по формуле G) и назвали их площадью. Но нужно еще доказать, что эти числа действительно  обладают свойствами, характеризующими площадь, и выяснить, для каких фигур эти числа определены.

Короче, нужно доказать, что они — те, о которых  говорится в теоремах I, II. Это мы дальше и докажем.

Попутно мы установим также основные свойства  внутренней и внешней площади.

 

Площади равных многоугольных фигур

Теорема 1. У равных многоугольных фигур  площади равны.

Доказательство проходит в три этапа.

Равенство площадей для параллельно  перенесенных фигур.

Лемма 1. Площадь прямоугольника со сторонами, параллельными линиям квадратной сетки, равна  произведению длин его сторон.

Доказательство получаем обычным путем, как в школьном курсе, беря квадраты, содержащиеся в данном прямоугольнике F и покрывающие его, т. е.

беря фигуры Fn и Fen. (Правда, в школьном курсе квадраты «накладывают» от двух сторон  прямоугольника, тут же они, вообще говоря, располагаются иначе.Но это несущественно.)

Лемма 2. Фигуры, составленные из равных  прямоугольников со сторонами, параллельными линиям сетки, имеют равные площади.

Доказательство. Из леммы 1 следует, что равные прямоугольники, о которых тут говорится, имеют равные площади. Следовательно, по  аддитивности площади, и фигуры,

составленные из них, имеют равные площади, что и  требовалось доказать. 

Лемма 3. Для  многоугольных фигур F всегда Fⁱ_nÌFÌF^e_n .

Это очевидно.

Замечание. Совершенно так же имеет место общее утверждение: Если фигура F состоит из внутренности

и ее границы, Fⁱ_nÌFÌF^e_n . Но если фигура имеет другое строение, то эти 

включения могут не выполняться. Простейший пример: если F—внутренность квадрата Q n-й сетки с добавленной стороной другого квадрата, то Fⁱ_n= F^e_n = Q, но Q Ë F и F Ë Q (рис. 25).

Лемма 4. Если одна многоугольная фигура  получается из другой параллельным переносом, то их  площади равны.

 

Равенство площадей многоугольных фигур,  получаемых отражением.

Лемма 5. Если фигура F' получается из  многоугольной фигуры F отражением в прямой, то она имеет ту же площадь, что и F.

Доказательство. Пусть F — данная  многоугольная фигура. Произведем отражение вкакой-нибудь прямой; обозначая его г, имеем фигуру F' = rF.

Вместе с фигурой F подвергнем тому же отражению все наши квадратные сетки. Получим, как указано вследствии леммы 4, такие же сетки, только  неизвестно, будет ли основной квадрат единичным. Если его площадь равна k> то все квадраты отраженных сеток будут тоже отличаться в k раз от площади соответствующих квадратов исходных сеток.

Доказательство теоремы 1. Теорема 1 о равенстве площадей равных многоугольных фигур непосредственно следует из доказанной леммы 5.

Действительно, фигура, равная данной, получается из нее некоторым перемещением, а всякое  перемещение может быть получено как результат нескольких (не более 3) последовательных отражений (теорема 1.3.5, ч. 3). При каждом отражении многоугольная фигура, согласно лемме 5, переходит в  многоугольную фигуру с той же площадью. Поэтому то же  будет и при нескольких отражениях. Тем самым  фигура, равная данной, имеет ту же площадь, что и требовалось доказать. 

Пусть выбран некоторый квадрат Е. Тогда каждой многоугольной фигуре F может быть отнесена, и притом единственная, численная площадь, т. е.  такое число S(F), что будут выполнены следующие четыре условия:

1) S(F) > О,

2) инвариантность,

3) аддитивность,

4) S(E)=l.

Если вместо квадрата Е взять другой Е`, то  соответствующие числа S' отличаются от S только общим множителем.

 

РОЛЬ И МЕСТО ПОНЯТИЯ «ПЛОЩАДЬ» В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ

Словом площадь школьники пользуются уже в начальной школе. Математика в начальных классах - это, прежде всего знакомство с основными математическими терминами, понятиями и величинами, одной из которых и является площадь. Однако, непосредственное введение понятия «площадь» и изучение площади как величины начинается только в пятом классе. Геометрический материал в I - VI классах распределен по всему курсу математики. Он составляет содержание так называемого пропедевтического курса геометрии. Основные цели этого курса - подготовить учащихся к сознательному усвоению систематического курса геометрии VII - IX классов. Задачами данного курса являются развитие у учащихся логического мышления, знакомство их с основными геометрическими понятиями, развитие пространственного мышления; формирование навыков измерения геометрических величин, построения геометрических фигур и т.д. Но и перейдя в пятый класс, учащиеся не сразу приступают к изучению площади. Это понятие вводится только во второй четверти. Как и в случае введения любого другого понятия, введению понятия «площадь» должно предшествовать изучение ряда объектов и понятий, на которые учащиеся опираются при изучении данного понятия. В нашем случае такими понятиями являются отрезок, длина отрезка, квадрат числа.

В школьных учебниках площадь многоугольника определяется с помощью указания ее свойств:

ü  численное значение площади любого много угольника всегда положительно;

ü  площади равных многоугольников, т.е. многоугольников, которые можно совместить с помощью движения, одинаковы;

ü  площадь многоугольника, полученного объединением двух многоугольников, не имеющих общих внутренних точек, равна сумме площадей составляющих многоугольников (многоугольники, не имеющие общих внутренних точек, будем называть не перекрывающимися);

ü  площадь квадрата со стороной единичной длины равна единице. В различных учебниках определения площади несколько отличаются друг от друга, но суть определений совпадает с указанным выше.

Геометрическая фигура называется простой, если ее можно разбить на конечное число плоских треугольников. Примером простой фигуры является выпуклый плоский многоугольник (рис.1).

 Выпуклый плоский многоугольник

Рис.1

В данном параграфе рассматриваются только плоские многоугольники.

Дадим определение площади для простых фигур.

Площадь простой фигуры — это положительная величина, численное значение которой обладает следующими свойствами.

Свойство 1. Равные фигуры имеют равные площади.

Свойство 2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.

Свойство 3. Площадь квадрата со стороной, равной единице измерения, равна единице.

Фигуры, имеющие равные площади, принято называть равновеликими.

Таким образом, площадь многоугольников можно трактовать как функцию S(F), заданную на множестве {F} всех многоугольников, принимающую числовые значения и обладающую следующими свойствами (их иногда называют аксиомами площади):

(положительность площади) для любого многоугольника F справедливо S(F) > 0;

(инвариантность площади) если, то символ «» здесь обозначает, что многоугольники и могут быть совмещены движением;

(аддитивность площади) если и многоугольники и не перекрываются, то S(F) = S(F2) + S(F2);

(нормированность площади) для квадрата Е со стороной единичной длины S(E) = 1.

Это определение по своему характеру сродни, например, определению арифметического корня: b -- есть неотрицательное число, n-я степень которого равна а.

Ведь и в этом случае арифметический корень b определяется указанием его свойств. Для корректного определения арифметического корня надо доказать, что такое число b, во-первых, существует и, во-вторых, единственно. Первое следует из того, что множество значений функции f(x) = хn ( и ) есть . Второе следует из строго монотонного возрастания рассматриваемой функции.

Для корректного определения площади многоугольников - функции S(F) -- требуется доказать, что такая функция существует и единственна.

Многим сам вопрос (об определении площади) покажется искусственным: они скажут, что площадь - первичное понятие, не подлежащее определению.

Взгляд на площадь как на первичное понятие сложился еще в древности. До недавнего времени этого взгляда придерживались и математики. На протяжении многих столетий они видели задачу в вычислении площадей; им не приходило в голову, что «площадь» нуждается в специальном определении.

Между тем их вычисления должны были на чем-то основываться -- если не на прямом определении, то на чем-то, его заменяющем, на каких-то принципах, которые позволяли им всякий раз получать в качестве площади определенное число. И такие принципы, конечно, существовали, хотя обычно не формулировались. Это - основные свойства площади. Так, в школьных учебниках площадь многоугольников вообще не определяется, но указываются ее свойства, соответствующие аксиомам площади, или определения носят формально дескриптивный характер, но свойства, определяющие площадь, используются не для построения общей функции S(F) (об этом речи нет), а для вычисления площади основных плоских фигур: прямоугольника, параллелограмма, треугольника, трапеции и плоских фигур, составленных из этих основных.

Познакомившись с понятием «площадь» в пятом классе и научившись измерять площадь плоских фигур непосредственно (путем подсчета единичных квадратов, умещающихся в данной фигуре), учащиеся сталкиваются с проблемой неточности при таком способе измерения. Здесь вводится так называемый косвенный метод измерения площади. То есть площадь не измеряется, а вычисляется по какой-то формуле. И поэтому на протяжении всего курса математики школьники учатся не измерять, а вычислять площади плоских геометрических фигур с помощью формул.

Площадь многоугольника и его свойства

Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Измерение площадей проводится с помощью выбранной единицы измерения аналогично измерению длин отрезков. За единицу измерения площадей принимают квадрат,сторона которого равна единице измерения отрезков. Квадратным сантиметром обозначается см². Аналогично определяется квадратный метр (м²), квадратный миллиметр (мм²) и т.д.

При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.

Обычно измеряют лишь некоторые связанные с многоугольником отрезки, а затем вычисляют площадь по определенным формулам.

Вывод этих формул основан на свойствах площадей, которые мы сейчас и рассмотрим.

Прежде всего отметим, что если два многоугольника равны, то единица измерения площадей и ее части укладываются в таких многоугольниках одинаковое число раз, т.е. имеет место следующее свойство:

1. Равные многоугольники имеют равные площади

Далее, пусть многоугольник составлен из нескольких многоугольников так, что внутренние области любых двух из этих многоугольников не имеют общих точек. Очевидно, величина части плоскости, занимаемой всем многоугольником, является суммой величин тех частей плоскости, которые занимают составляющие его многоугольники. Итак:

2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

Свойства 1 и 2 называют основными свойствами площадей. Аналогичными свойствами обладают и длины отрезков.

Наряду с этими свойствами нам понадобится еще одно свойство площадей.

3. Площадь квадрата равна квадрату его стороны

Краткую формулировку этого свойства следует понимать так: если сторона квадрата при выбранной единице измерения отрезков выражается числом а, то площадь этого квадрата выражается числом а².

МЕТОДИКА ИЗУЧЕНИЯ ДАННОЙ ТЕМЫ

На протяжении всего курса математики школьники учатся измерять площади плоских геометрических фигур. И чем больше различных геометрических фигур знают учащиеся, тем больше различных формул и способов вычисления площади им необходимо и тем больший математический «арсенал» для этого нужно задействовать. Возьмем, к примеру, прямоугольник. Для вычисления его площади необходимо всего лишь уметь умножать:. То же самое и в случае параллелограмма:. Далее: треугольник: — уже немного сложнее. При вычислении площади круга учащимся нужно уметь находить квадрат числа и знать отношение длины окружности к ее диаметру:. Площадь параллелограмма и треугольника можно вычислить и другим способом, но для этого нужно знать тригонометрию. Еще одним простым алгоритмом нахождения площади треугольника является формула Герона. Для ее реализации учащиеся должны уметь извлекать квадратный корень из числа. Наиболее универсальной из всех школьных формул для вычисления площади является интегральная формула площади криволинейной трапеции:. Но она и наиболее сложна — интегрирование часто вызывает у учащихся некоторые затруднения.

 Знакомство с понятием площади

Как уже упоминалось выше понятие площади (и ее измерения) базируется на ряде других понятий. Знакомство с площадью в пятом классе начинается с изучения площади прямоугольника. Учащимся предлагается конструктивное определение площади. Хотя определением его назвать можно с трудом, скорее это правило нахождения площади прямоугольника: «Чтобы найти площадь прямоугольника нужно умножить его длину на ширину"[7] (стр123). То есть уже здесь, на самом первом этапе знакомства с площадью, ее не измеряют, а находят, вычисляя по какому-то алгоритму, какой-то формуле. И уже на этом этапе учитель должен заострить внимание учащихся на том, что площадь необходимо вычислять. И действительно: до этого все мы могли измерять путем непосредственного сравнения с единичной величиной. Для этого есть специальные измерительные инструменты. Чтобы измерить длину отрезка мы брали в руки линейку, для измерения градусной меры угла пользовались транспортиром, массу определяли с помощью весов, а вот для измерения площади таких удобных инструментов нет. Хотя в некоторых случаях учителя используют на своих уроках для измерения площади палетки (прозрачную пленку, расчерченную на клетки). Палетка действительно является инструментом для измерения площади, ведь с ее помощью мы находим площадь фигуры путем сравнения ее с единичной. С методической точки зрения этот инструмент очень хорош на начальной стадии изучения площади, так как помогает ученикам понять саму идею измерения площади, а именно подсчет числа единичных квадратов умещаемых в данной фигуре. Но палетка инструмент не точный и далеко не универсальный, к тому же пересчитывать квадратики — дело весьма утомительное. Именно поэтому чтобы найти площадь ее нужно не измерить, а вычислить.

Но вернемся к «подготовке» учащихся к изучению площади. Основными опорными понятиями, которыми должны владеть учащиеся, чтобы успешно усвоить данную тему являются отрезок, длина отрезка, квадрат числа, формула. К умениям необходимым для изучения данной темы можно отнести умение измерять длину отрезка, производить простейшие алгебраические операции над натуральными числами.

Если с усвоением понятий «отрезок», «длина отрезка» и операции над числами особых трудностей у учащихся не возникает, то с понятиями «квадрат числа» и «формула» дело обстоит немного сложнее.

При работе с формулами у учащихся могут возникнуть трудности в тех случаях, когда одна буква в формуле должна быть заменена каким-либо выражением. (Поэтому следует особое внимание уделить работе с формулами).

В пятом классе при изучении площади прямоугольника учащиеся, помимо единиц измерения площади получают представление об измерении площади подсчетом единичных квадратов. Умножение числа квадратов, укладывающихся в длину прямоугольника на число квадратов в ширину — простой и быстрый способ сосчитать квадраты в прямоугольнике.

Ключевым свойством площади на данном этапе изучения является ее аддитивность. «Площадь всей фигуры равна сумме площадей ее частей» [7](стр123). Именно на аддитивности площади основываются большинство формул для ее вычисления, начиная формулой площади треугольника и заканчивая интегральной формулой для вычисления площади криволинейной трапеции. На отработку этого свойства площади следует обратить особое внимание, в школьных учебниках для этого имеется множество задач. Уже в пропедевтическом курсе математики пятого класса рассматривается задача о площади:

Найдите площадь двухкомнатной квартиры, если площадь обеих комнат 35 м², площадь кухни 9 м², а подсобные помещения занимают общую площадь, а м2. Составьте выражение для решения задачи и найдите его значение при, а = 8, а = 12.

С методической точки зрения данная задача направлена на то, чтобы развить у учащихся навыки работы с формулами и, параллельно дать им представление об одном из основных свойств площади.

 Площадь прямоугольника

С площадью прямоугольника учащиеся знакомятся, уже изучая математику в пятом классе, но более детальное ее рассмотрение начинается в курсе геометрии восьмого или девятого класса. И в обоих случаях площадь прямоугольника рассматривается как часть темы «Площадь многоугольника».

В пятом и шестом классе уже изучалась площадь прямоугольника и площадь круга, но ни определения площади, ни ее свойств рассмотрено не было. Теперь же учащимся предлагается определение площади как величины той части плоскости, которую занимает многоугольник, и рассматриваются некоторые свойства площади:

1) Равные многоугольники имеют равные площади.

2) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. (В учебнике эти два свойства названы основными).

3) Площадь квадрата равна квадрату его стороны.

На основе этих трех свойств доказывается теорема о том, что площадь прямоугольника равна произведению его смежных сторон.

Тема площади прямоугольника играет важную роль в изучении площади вообще, так как служит основой для вывода площади треугольника, параллелограмма и др.

Площадь параллелограмма

Вывод формулы площади параллелограмма сводится к построению прямоугольника, равного данному параллелограмму по площади. Примем одну сторону параллелограмма за основание, а перпендикуляр, проведенный из любой точки противолежащей стороны на прямую, содержащую основание будем называть высотой параллелограмма. Тогда площадь параллелограмма будет равна произведению его основания на высоту.

Пользуясь соотношениями между углами и сторонами треугольника можно вывести еще одну формулу для вычисления площади параллелограмма:

Воспользуемся только что полученной формулой и выразим высоту ВН через сторону АВ. В прямоугольном треугольнике АВН ВН — катет, лежащий против угла А, АВ — гипотенуза. Тогда. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Вывод формулы площади параллелограмма в первом случае основан на теме «площадь прямоугольника» и основных свойствах площади, во втором случае — на тригонометрических соотношениях, поэтому для успешного усвоения этих формул необходимо повторить ранее изученный материал.

Площадь параллелограмма

Основание – одна из сторон параллелограмма

Высота параллелограмма – перпендикуляр, проведенный из любой точки

Противоположной стороны к прямой, содержащей основание.

Теорема

Площадь параллелограмма равна произведению его основания на высоту.

Доказательство:

Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD

за основание и проведем высоты BH и CK (см. рис.). Докажем, что S = ADBH.

Докажем сначала, что площадь прямоугольника HBCK также равна S.

Трапеция ABCK составлена из параллелограмма ABCD и треугольника ABH.

Но прямоугольные треугольники DCK и ABH равны по гипотенузе и острому углу(их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямыхAB и CD секущей AD), поэтому их площади равны.

Следовательно, площади параллелограмма ABCD и прямоугольника HBCKтакжеравны, т.е. площадь прямоугольника HBCK равна S. По теореме о площади прямоугольника S = BCBH, а так как BC = AD, то S = ADBH. Теорема доказана.

Площадь треугольника

Существует несколько формул для вычисления площади треугольника. Рассмотрим те, что изучаются в школе.

Первая формула вытекает из формулы площади параллелограмма и предлагается учащимся в виде теоремы: площадь треугольника равна половине произведения его основания на высоту.

Важно обратить внимание учащихся на два следствия, вытекающих из данной теоремы. А именно:

1) площадь прямоугольного треугольника равна половине произведения его катетов.

2) если высоты двух треугольников равны, то их площади относятся как основания.

Эти два следствия играют важную роль в решении разного рода задач. С опорой на данную доказывается еще одна теорема, имеющая широкое применение при решении задач: если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы.

Вторая формула тоже связана с параллелограммом: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Существует несколько способов доказательства этой формулы и один из них — достраивание треугольника до параллелограмма.

Тема «Площадь треугольника» имеет большое значение в школьном курсе математики. Треугольник — простейшая из геометрических фигур. Он является «структурным элементом» школьной геометрии. Подавляющее большинство геометрических задач сводятся к решению треугольников. Не исключение и задача о нахождении площади правильного и произвольного n-угольника.

 Площадь круга

Формула для вычисления площади круга вводится в VI классе. Перед тем, как записать формулу для площади круга, учащиеся выясняют зависимость между длиной окружности и ее диаметром. Важно, обратить внимание учащихся на отношение, (- длина окружности, а — ее диаметр) и показать, что для любой окружности значение выражения= - есть величина постоянная, приближенно равная 3,14.

 Площадь произвольного n-угольника

Отдельно в школе площадь произвольного многоугольника не рассматривается. Однако, в курсе геометрии есть ряд задач, в которых требуется найти площадь произвольного многоугольника. К тому же на практике задача о площади такого многоугольника встречается довольно часто. Поэтому на уроках геометрии следует уделить должное внимание решению подобных задач. Методическая ценность такого рода задач заключается в том, что они, во-первых, хорошо иллюстрируют свойство аддитивности площади, а, во-вторых, помогают учащимся развить навыки нахождения площади треугольника различными способами.

Итак, основная идея нахождения площади произвольного n-угольника — это разбиение его на конечное число треугольников. В результате суммирования площадей треугольников, составляющих данный n-угольник получается искомая площадь. Нахождение площади n-угольника таким способом лежит в основе доказательства теоремы о площади трапеции.

 

 

 

Заключение

Теперь попытаемся подытожить и обобщить все вышесказанное. Среди различных систем величин, изучаемых в школе на различных этапах обучения, учащиеся уже в начальной школе знакомятся с понятием площади плоской фигуры. На первых этапах обучения речь идет об интуитивном представлении о площади, а не о строгом математическом обосновании этого понятия.

Первоначально у учащихся представление о площади плоской фигуры связывается с подсчетом числа единичных квадратов. Изучение площади в школе начинается с рассмотрения площади прямоугольника (стороны которого соизмеримы с линейной единицей измерения). Программа курса геометрии предусматривает знакомство учащихся с вычислением площади с помощью палетки. Использование ее позволяет сделать не только доступным для учащихся изучение вопроса об измерении площади любой плоской фигуры, но и помогает им правильно понять идею измерения площади (подсчет числа единичных квадратов, помещающихся в данной фигуре). Переходя от непосредственного измерения площади путем сравнения ее с единицей измерения к способам косвенного измерения площадей, учителю необходимо обратить внимание учащихся на то, что для измерения площадей нет столь удобных приборов, какие были для измерения длин отрезков и величин углов. Поэтому стоит более внимательно разобраться с величиной — площадью и выявить способы ее нахождения.

Сравнивая свойства площади со свойствами таких величин, как расстояние, угол, мы убеждаемся в том, что:

а) площади можно складывать между собой и умножать на положительные числа;

б) за единицу измерения площади можно выбрать некоторую площадь S, где S=ku, где k — некоторое число, u — единица площади.

С понятием «Площади фигур» впервые учащиеся знакомятся в курсе геометрии V класса. Понятие площади фигуры вводится аксиоматически, но делается это неявно, с опорой на жизненный опыт учащихся. Сначала вводится формула площади прямоугольника (с целыми длинами сторон; длины сторон — конечные десятичные дроби; длины сторон — бесконечные десятичные дроби). На ее основе выводится формула площади параллелограмма; последняя выводится при выводе формул площади треугольника:; (вводится немного позднее);, трапеции, выпуклого многоугольника, описанного около круга; должное внимание уделяется формуле площади круга; формула выводится неявно на уровне наглядных представлений; VII — IX классы — основа — предельный переход от площади правильных вписанных и описанных n-угольников к площади круга. Рассматриваются такие площади подобных фигур: зависимость площади подобных фигур от отношения их линейных размеров; соответствующее соотношение выводится и для простых фигур с помощью разбиения их на конечное число треугольников.

 

 

 

 

 

 

 

 

 

Литература

1. Александров А.Д. Геометрия: Учеб.пособие. / Александров А.Д., Нецветаев Н.Ю.– Москва: Наука, 1990. – 672 с.

2. Антонов Н. П., Выгодский М. Я., Никитин В. В., Санкин А. И. Сборник задач по элементарной математике. — Москва: Наука, гл. ред. Физ. -мат. лит., 1972.

3.  Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия: Учеб.для 7 — 9 кл. ср. шк. — 4-е изд. — Москва: Просвещение, 1994.

4. Башмаков М. И. Алгебра и начала анализа: Учеб.для 10 — 11 кл. ср. шк. — 2-е изд. — Москва: Просвещение, 1992.

5. Блох А. Я.  Методика преподавания математики в средней школе: Учеб.пособие для студ. пед. ин-тов по физ.-мат. спец./ Блох А. Я., Гусев В. А., Дорофеев Г. В. и др.  — Москва: Просвещение, 1987.

6. Блох А. Я. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов пед. ин-тов по спец. 2104 «Математика» и 2105 «Физика»/ Блох А. Я., Канин Е. С., Килина Н. Г. и др.. — Москва: Просвещение, 1985.

7. Виленкин Н. Я. Математика: Учеб.для 5 кл. ср. шк./ Виленкин Н. Я., Чесноков А. С., Шварцбурд С. И. и др. — 2-е изд. Москва: Просвещение, 1992.

8. Корешкова Т. А. Многоугольники и их площадь в школьном курсе математики. //Математика в школе, с. 70 — № 3 — 2003.

 

 

Скачано с www.znanio.ru