
Определенный интеграл. Формула Ньютона-Лейбница
Цели:
· Образовательные:
o сформировать понятие интеграла;
o формирование навыков вычисления определенного интеграла;
o формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.
· Развивающие:
o развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
· Воспитательные:
o активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Ход урока
1.Организационный момент (сообщение темы и цели урока).
2. Мотивация урока.
Понятие определенного интеграла является одним из основных понятий математики. К концу 17 в. Ньютоном и Лейбницем был создан аппарат дифференциального и интегрального исчисления, который составляет основу математического анализа.
На предыдущих занятиях мы научились “брать” неопределенные интегралы, вычислять определенные интегралы. Но куда важнее применение определенного интеграла. Мы знаем, что с его помощью можно вычислять площади криволинейных трапеций. Сегодня мы ответим на вопрос: “Как это сделать?”
3. Актуализация опорных знаний. Проверка д/з.
Фронтальный опрос:
1. Что называется интегралом?
2. Что называется первообразной?
3. Как читается основное свойство первообразной?
4. Верно ли, что интеграл от любой степенной функции будет снова степенной функцией?
5. F'(х) — f(x) - как это можно прочесть?
Найти неопределённый интеграл
![]()
![]()
![]()
![]()
![]()
![]()
Является
ли функция ![]() первообразной для функции
первообразной для функции ![]() на
промежутке
на
промежутке ![]()
№3.
Для функции ![]() найдите первообразную, график которой
пересекает ось
найдите первообразную, график которой
пересекает ось ![]() в точке с абсциссой 4.
в точке с абсциссой 4.
4. Изучение нового материала (Формирование новых понятий и способов действий)
|
Определение: Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b]. Интегралом от функции f(x) на [a;b] называется площадь её криволинейной трапеции. |
|
|
Обозначение: Читается: «интеграл от a до b эф от икс дэ икс» |
|
|
Формула Ньютона-Лейбница
|
|
|
Пример 1. Вычислить
определённый интеграл: |
|
|
Переходим к вычислению площадей плоских фигур с помощью определенного интеграла. Кроме умения вычислять определенный интеграл, нам нужно вспомнить свойства площадей. В чем они заключаются? · Равные фигуры имеют равные площади. · Если фигура разбита на две части, то её площадь находится как сумма площадей отдельных частей. Пример 2. Вычислить
площадь фигуры, ограниченной линиями
|
|
5. Закрепление изученного материала
1 уровень сложности. Вычислите интегралы и выберите вариант ответа:
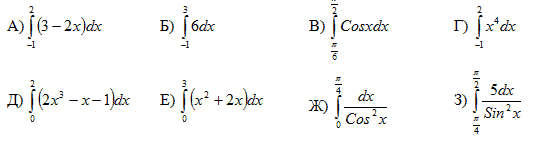
|
Ответы: |
а) 4; |
б) 18; |
в) 1; |
г)6; |
д) 0,5; |
е) 5; |
ж) 12; |
з) 6,6 |
2 уровень сложности. Вычислите площадь фигур, ограниченных линиями:
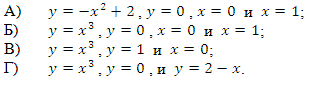
3 уровень сложности. При каких a будет верно равенство:
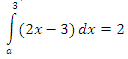
Зарядка для глаз.
6. Историческая пауза.
Понятие интеграл непосредственно связано с интегральным исчислением – разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления.
Более близко и точно к понятию интеграл подошел Исаак Ньютон. Он первый построил дифференциальное и интегральное исчисления и назвал его "Методом флюксий..." (1670-1671 гг., опубл. 1736 г.). Переменные величины Ньютон назвал флюентами (текущими величинами, от лат. fluo – теку). Скорости изменения флюент Ньютон – флюксиями, а необходимые для вычисления флюксий бесконечно малые изменения флюент – "моментами" (у Лейбница они назывались дифференциалами). Таким образом, Ньютон положил в основу понятия флюксий (производной) и флюенты (первообразной, или неопределённого интеграла).
Это сразу позволило решать самые разнообразные, математические и физические, задачи.
Одновременно с Ньютоном к аналогичным идеям пришёл другой выдающийся учёный – Готфрид Вильгельм Лейбниц.
Размышляя над философскими и математическими вопросами, Лейбниц убедился, что самым надежным средством искать и находить истину в науке может стать математика. Знак интеграла (∫), был впервые использован Лейбницем в конце XVII века. Этот символ образовался из буквы S — сокращения слова лат. summa (сумма).
Ньютон и Лейбниц разработали две трактовки понятия обычного определенного интеграла.
Ньютон трактовал определенный интеграл как разность соответствующих значений первообразной функции:
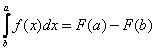 , где F`(x)=f(x).
, где F`(x)=f(x).
Для Лейбница определенный интеграл был суммой всех бесконечно малых дифференциалов.
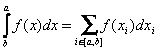 .
.
Формулу, которую открыли независимо друг от друга Ньютон и Лейбниц назвали формула Ньютона – Лейбница.
Таким образом, понятие интеграл было связано с именами знаменитых ученых: Ньютон, Лейбниц, Бернулли, положивших основу современного математического анализа.
7. Самостоятельная работа.
Вычислите определённые интегралы и вы узнаете одно из высказываний французского математика С.Д.Пуассона.
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
Жизнь |
-1 |
Тремя |
-16 |
|
Двумя |
1 |
Вещами |
7 |
|
Занятием |
|
И |
0 |
|
Математикой |
6 |
Арифметикой |
|
|
Преподаванием |
0 |
Её |
3 |
|
Украшается |
|
Забыванием |
0 |
8.Итоги урока. Рефлексия. Д/з.
Выучить_____ Решить №__________
Оценить степень сложности урока.
Вам было на уроке:
· легко;
· обычно;
· трудно.
Оцените степень вашего усвоения материала:
· усвоил полностью, могу применить;
· усвоил полностью, но затрудняюсь в применении;
· усвоил частично;
· не усвоил.
Опорный конспект по теме «Интеграл. Формула Ньютона-Лейбница».
|
Определение: Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b]. Интегралом от функции f(x) на [a;b] называется площадь её криволинейной трапеции. |
|
|
Обозначение: Читается: «интеграл от a до b эф от икс дэ икс» |
|
|
Формула Ньютона-Лейбница
|
|
|
Пример 1. Вычислить
определённый интеграл: Решение: |
|
|
Пример 3. Вычислить
площадь фигуры, ограниченной линиями Решение:
|
|
|
Пример 3. Вычислить
площадь фигуры, ограниченной линиями
|
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.