«Определенный интеграл и его свойства».

Урок по алгебре и началам анализа в 11 классе,

по теме «Определенный интеграл и его свойства».

Тип урока: комбинированный урок

Цели урока:

1.   Сформировать умения применять правило вычисления определённого интеграла;

2.     Ввести формулу Ньютона-Лейбница;

3.     Сформировать умение вывода основных свойств определенного интеграла; отработать навыки вычисления  определенных интегралов.

4.   Продолжить формирование у учащихся навыков само и взаимоконтроля.

Структура  урока:

1.Организационный момент.

2.Постановка целей и задач  урока.

3.Актуализация опорных знаний.

4. Изучение нового материала.

5.Закрепление изученного материала.

6.Задание на дом.

7. Итог урока.

Ход урока.

1.Организационный момент

2.Постановка целей и задач  урока. 

Приветствие, сообщение темы и задач урока. Учащиеся записывают тему урока.

3. Актуализация опорных знаний.

  В качестве актуализации опорных знаний предлагается провести небольшую самостоятельную работу с последующей самопроверкой. Рекомендуется организовать работу двух учащихся на обратной стороне доски, а затем учитель комментирует решение и получившиеся ответы.

Работа дифференцированная, задания 4 и 5 повышенной сложности.

4. Изучение нового материала:

План лекции:

1.Понятие определенного интеграла. Формула Ньютона-Лейбница.

2.Основные свойства определенного интеграла.

3.Примеры.

Определенным интегралом  в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной  F(x) при изменении аргумента х от значения х=а до х=в:

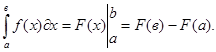
Данная формула  так же  называется формулой Ньютона-Лейбница, ее называют основной формулой интегрального исчисления.

Свойства определенного интеграла.

1. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:
2. Постоянный множитель можно выносить за знак определенного интеграла:
3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный:
4. Определенный интеграл с одинаковыми пределами равен нулю:
5. Отрезок интегрирования можно разбивать на части:  

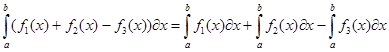
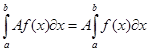
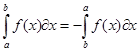
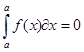
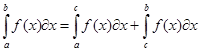
ПРИМЕРЫ: Вычислить интеграл:

1);

2) ;

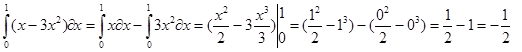3) ;

4) ;

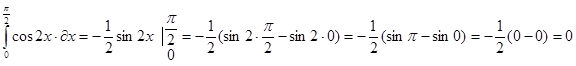5. Закрепление изученного материала.

Работа организуется в парах, с последующей взаимопроверкой.

6.Задание на дом.

Домашнее задание предлагается дифференцированное: 1-5 задания для обязательного выполнения, задания 6*-8* на дополнительную оценку

7. Итог урока.

Учитель дает общую характеристику работы класса и отдельных учащихся, объявляет оценки за работу на уроке.

Приложение:

Ответы к самостоятельной работе:

Ответы к работе в парах: