Актуальность:

- возрастающие требования к подготовке учащихся на фоне низкой мотивации

- изложение школьных предметов разрознено и самостоятельно, нет единой логики, способной построить общую картину мира;
- предъявляются высокие требования к математическому образованию школьников на фоне  недостаточной сформированности общеучебных умений;
-возрастает практическая значимость школьного курса математики.

Теоретическое обоснование: в ходе опыта разрабатывается система интегрированных уроков  с широким использованием межпредметных связей, внеклассных мероприятий на  основе концепции интеграционного обучения.

Ведущая идея опыта:

- создание на уроках условий для успешной, активной и сознательной деятельности учащихся, основанной на установлении межпредметных связей, проведении систематизации понятий и явлений, формировании естественно - научного метода исследований;

- формирование комплексного подхода к учебным предметам, единого с точки зрения естественных наук взгляда на ту или иную проблему, отражающую объективные  связи в окружающем мире

- расширение кругозора учащихся

 - повышение интереса к практической значимости предмета.

- развитие у учащихся представлений о ведущей роли математики в умственном развитии человека;

Технология опыта:

      Я  работаю над проблемой : « Развитие творческих способностей учащихся».

Одно из направлений проблемы это: « Интегрированные уроки как один из способов достижения метапредметных результатов»

. Эта  проблема стала для меня   актуальной потому, что в работе явно увидела недостаточную глубину и осознанность усвоения учащимися программного материала, разрозненное восприятие содержания учебных программ. Ученики очень часто задают вопрос «А, в жизни,  зачем это надо? Как это применяется?». Ребята не видят связь математики с жизнью, а между тем именно построение математической модели является фундаментальным в развитии науки, методы исследований, применяемые в математике,  распространяются во все сферы жизни. Еще Рене Декарт писал, что любая жизненная задача может быть сведена к математической и разрешима с помощью уравнений.

       Изложение школьных предметов настолько  разрозненно и самостоятельно, что ученик не видит единой логики, не способен построить общую картину мира. Скорость, с которой движется   тело» в физических задачах,  и «скорость движения легкового автомобиля» в математической задачке кажутся для него совершенно разными понятиями. Не секрет, что зачастую, учащиеся не могут использовать известные факты из математики на уроках физики, химии, информатики и т.д., и наоборот, при решении математических задач, очень затрудняет работу присутствие в задачах физического и другого специфического содержания. «Сегодняшнее школьное, да и вузовское образование дает разрозненную картину мира, изучение фактов, а не их взаимосвязей и построение собственных логических теорий и решение практических задач; дает в большинстве случаев результат невозможности построения человеком собственных моделей в жизненных ситуациях

         В наши дни реальной необходимостью становится непрерывное образование, что требует полноценной базовой математической подготовки. Одна из основных целей обучения математике в школе – овладение математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования. Поэтому я поставила задачу актуализации практической значимости математических знаний, через систему интегрированных уроков, развития у школьников нравственных представлений о природе математики, месте математики в системе наук и роли математического моделирования в научном познании и практике.

Образовательные и воспитательные задачи обучения математике должны решаться комплексно. Важным условием правильной организации учебно-воспитательного процесса является выбор рациональной системы методов и приёмов обучения, её оптимизация с учётом возраста учащихся, уровня их математической подготовки, развития общеучебных умений. В зависимости от указанных факторов необходимо реализовывать сбалансированное сочетание традиционных и новых методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, использование технических средств.

         Важно сформировать на уроках математики целостное восприятие решаемой задачи, умение проводить выбор методов решения, перенос и использование знаний, умений, навыков с одной учебной дисциплины на другую, узнавание и применение фактов из смежных дисциплин (физика, , информатика).

         Данную проблему, на мой взгляд,  можно разрешить, включая в преподавание курса математики интегрированные уроки (математика + физика, математика + история, математика + информатика), либо используя отдельные приёмы, которые позволяют продемонстрировать взаимопроникновение дисциплин, междисциплинарные связи, научить комплексно использовать школьные знания.

          В условиях повсеместной информатизации особенно актуальным становится формирование понимания единства и разнообразия подходов к решению одних и тех же задач методами математического анализа и с помощью информационных технологий, кроме того, применение компьютера на уроке дает возможность наглядно и ярко представить содержание материала, дает возможность для проведения исследовательской работы учащихся.

 Интегрированное обучение – это проведение:

 -  бинарных уроков,

 -  уроков с широким использованием межпредметных связей

 -  проведение внеклассных мероприятий по предметам.

         Использование межпредметных связей на уроках

         Учащиеся   с большим интересом воспринимают сведения о  применении математической теории на практике. Например, при  изучении показательной функции можно рассказать о совсем необычных областях   ее применения. У Жюля Верна описан случай.

         Готовился к спуску на воду небольшой корабль, с парусами в форме трапеции, - трабоколо. Когда уже начали выбивать клинья из - под киля, в гавань влетела нарядная яхта. Спустившееся на воду судно должно было неминуемо врезаться в яхту. «Вдруг из толпы зрителей выскакивает какой-то человек. Он хватает канат, висящий на носу трабоколо….Поблизости  врыта в землю швартовая пушка. Матифу набрасывает на нее канат и обматывает несколько раз… канат начинает медленно разматываться. Но силач сдерживает корабль, рискуя быть раздавленным. Это длиться 10 секунд. Наконец канат лопнул. Тракоболо прошло за кормой яхты на расстоянии более фута.»

        Объяснить этот факт очень просто. После одного оборота каната вокруг столба сила F, приложенная к одному концу каната удерживает в К раз большую силу , приложенную к другому концу каната, причем после каждого оборота удерживаемая сила возрастает в К раз. Для пенькового каната и деревянного столба К=2^2π/1,75. Поэтому ,оборачивая канат вокруг столба 3 раза получаем увеличение в 2^6π/1,75=1800 раз. Будем считать примерную силу, необходимую, чтобы остановить корабль 400000Н. Составим уравнение 400000=1800F₀, откуда  F₀=220Н. что эквивалентно 22кг. Приложить силу в 22кг. может любой взрослый человек.  Это явление мы используем ежедневно, например, завязывая шнурки (узел- это веревка, обвитая вокруг другой веревки, узел крепче, чем больше одна часть обвивается вокруг другой).

        Рассказывая об экспоненте, я привожу пример с цепочкой: если держать гибкую цепь за оба конца, то она провиснет по кривой, которая называется цепной линией:

У = 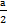 (е^х/а+е^-х/а), этим же уравнением описывается сечение паруса, надутого ветром, «паутинки, усеянные крохотными капельками утреннего тумана, провисают, образуя под тяжестью груза цепные линии, стоит лишь лучу солнца проникнуть сквозь туман, как паутина начинает переливаться всеми цветами радуги, превращаясь в сверкающую гроздь бриллиантов, и  число е предстает пред нами во всем своем великолепии» (Ж.А.Фарб –энтомолог «Жизнь паука»).

        Музыка и звезды связаны логарифмами: яркость звезд  оценивается в логарифмической таблице с логарифмом 2,5; а шум измеряется в децибелах, которые определяются по логарифмической шкале с основанием 10.

        Раковины моллюсков, улиток, рога горных козлов, наша Галактика – закручены по логарифмической спирали, так как  спираль является математическим символом соотношения формы роста. В.И.Гете считал ее даже символом жизни и духовного развития.

       Такая информация помогает заинтересовать  ребят изучаемым материалом, поэтому  на итоговом, зачетном, уроке, посвященном изучению показательной функции, мы рассматриваем  ее применение в биологии, экологии, экономике, физике, статистике. Сообщения готовят  сами учащиеся, подготовительная работа к этому уроку требует от ребят способности пользоваться дополнительными источниками информации: научно-познавательной литературой, интернетом, развивает их коммуникативные способности.  При проведении урока используется групповая форма работы.

        В старшей школе при изучении тем «Производная» и «Превообразная»  использование межпредметных связей,  считаю, является необходимым условием, так как помогает понять не только суть многих природных явлений, но и  причину появления дифференциально-интегрального исчисления.

         Вот пример трех задач построенных на основе одной математической модели:

1.Найти площадь фигуры, ограниченной кривой у=6х-х² и осью абсцисс.

2.Тело движется прямолинейно со скоростью v =  6t-t² (м/с). Найти длину пути, пройденного телом до начала остановки.

3.По цепи идет переменный ток I=6t-t² (А). Найти величину заряда, прошедшего по цепи за первые 6с.

          При изложении темы о нахождении наибольшего или  наименьшего значения функции,  обязательно упоминаю о принципе П.Ферма, согласно которому,  природа заставляет все,  или почти все явления, совершаться с наименьшей затратой времени, энергии и др.

В курсе математики VI класса рассматриваются столбчатые и круговые диаграммы, вычисляют среднее арифметическое, читают графики. И все это как нельзя, кстати, для получения среднемесячной, среднегодовой температур воздуха, а для вычисления расстояния между двумя точками координатной оси - нахождения амплитуды температуры воздуха. Ребята учатся отвечать на вопросы, используя графики зависимости температуры от времени года, от высоты. Чтобы увидеть наглядное представление о количестве осадков в течение года и по месяцам, строят столбчатые и круговые диаграммы.

           В математике при знакомстве с геометрией дети изучают фигуры, углы. Важность геометрии, геометрических тел в природе очень велика. И живые примеры можно привести из географии. Для детей открытием является то, что Пифагор первым сделал интереснейшее предположение, что Земля - шар. "Все в природе должно быть совершенно и гармонично. Но совершеннейшее из геометрических тел есть шар. Земля тоже должна быть совершенна. Стало быть, Земля - шар!" - говорил Пифагор.

           Так же при изучении курса стереометрии использую имеющиеся у учащихся знания о земном шаре. При рассмотрении окружности большого круга, проведённой через две точки шаровой поверхности, подчёркиваю, что на шаровой поверхности линия кратчайшего расстояния между точками идёт всегда по дуге большого круга. На земной поверхности такие линии называют ортодромами. Они имеют большое практическое значение в морской и воздушной навигации: ведь выгоднее всегда двигаться по направлению кратчайшего расстояния.

корабля).

            Географические координаты точек земной поверхности – широта и долгота – учащимся уже известна по урокам географии. После этого даю понятие о координатах точек плоскости.

           А заключительное занятие по теме «Прямоугольная система координат» проходило как внеклассное мероприятие: «Знаки небес» (астрономия+математика). Слушая легенды древней Греции о Большой и Малой Медведице, о Персее, Кассиопее и Андромеде ребята изображали эти созвездия на системе координат, кроме того они узнали много очень интересного о своих зодиакальных знаках, о чертах об особенностях характера тех, кто родился в одном тригоне, и смогли изобразить свое созвездие.

          При изучение темы “Масштаб” в VI классе проводила урок, где были рассмотрены понятия числового и линейного масштаба, ознакомила учащихся с приёмами перевода числового масштаба географических карт в линейный и наоборот. Попутно учащимся были предложены задачи и упражнения по географии.

          Практическое применение числового масштаба было проиллюстрировано на примерах определения расстояния между двумя пунктами, изображёнными на топографических картах с разными масштабами; длины отрезка, необходимого для изображения расстояния между пунктами по карте по заданному истинному расстоянию между ними и числовому масштабу карты; числового масштаба карты по расстоянию между заданными пунктами на карте и истинному расстоянию между ними.

         Совместно с учителем истории и физики разработали ряд интегрированных уроков.

          В процессе своей работы зафиксировала рост познавательного интереса учащихся к предметам под влиянием межпредметных связей. Межпредметные связи стимулируют тягу к знаниям, укрепляют интерес к предмету, расширяют заинтересованность, углубляют знания, способствуют становлению интересов профессионального плана

Уроки истории — это гуманитарные уроки. На уроках истории, где происходит обмен опытом между поколениями и культурами, происходит патриотическое воспитание учащихся, достигается свобода в суждениях и ответах. А так как история связана со многими предметами, то интеграция уроков истории приобретает особую актуальность. Интегрированные уроки предоставляют и учителю, и ученику больше возможности для интеллектуального творчества и овладения сложным материалом. Согласно  классификации тенденций развития образовательных технологий, интегрированный урок относится к группе технологий «воспитания в процессе жизни», которая представляет собой стремление уйти от школярского подхода к образованию, крайней дифференциации предметного обучения и привести его в естественную органическую связь с жизнью.

 Ролью ученика на интегрированном уроке является не воспроизведение и пересказ знаний, почерпнутых из учебника или от учителя, а выработка индивидуального пути освоения и применения этих знаний. К ученику как к участнику процесса предъявляются следующие требования:

Умение находить и обрабатывать информацию, используя различные источники, навыки критического рассмотрения и осмысления полученной информации, умение предъявлять и обсуждать собственные выводы, сделанные на основе полученной информации, вступать в дискуссию, выслушивать и принимать во внимание аргументированные выводы других, выступать публично, литературно выражая свои мысли.

Межпредметные связи способствуют формированию личности школьника как субъекта познания и обучения .

В основе предметно - классно- урочной системы обучения лежит предъявление содержания образования в виде учебных предметов, построенных на науках, дифференцированно изучающих мир. Это деление познания на научные области возникло по немощи человека познать мир целиком во всех его связях и отношениях. Предметная дифференциация облегчает процесс познания, но сказывается на его качестве. У учащихся возникает клочкообразное представление о мире и его законах, в которых не всё связано и зависимо и многое существует само по себе. Такое внесистемное знание портит мышление и искажает отношение к миру и самому себе. Так возникает потребность на уровне обучения в объедении знаний разных наук об одних и тех же объектах действительности, т.е. потребность межпредметных связях учебных дисциплин.  Наиболее тесно работаю в паре с учителем истории

Лавренюк Н.В..

Разрабатывая уроки истории надо помнить, что их идея может зависеть не только от материала программы и педагогической задачи, стоящей перед учителем, но и временем, когда программный материал усваивается.

Замысел урока призван учитывать современное состояние культурной обстановки в обществе, сегодняшнее восприятие жизни учащимися, ибо то, что сегодня кажется не интересным учителю историку, почти наверняка будет не актуальным для учеников.

Готовясь к урокам, следует ориентироваться и на самого себя. Лучше если замысел урока будет интересен лично учителю. И тогда знакомый уже достаточно «приевшийся» материал будет раскрыт по-новому. В процессе подготовки урока вырисовываются и другие его компоненты: повторение усвоенного на предыдущих занятиях, закрепление материала в сознании учащихся, характер домашнего задания. В это время происходит подбор материала к конкретной теме, разработка вопросов, постановка проблемных заданий, которые помогут рассмотреть тему с разных точек зрения.

В процессе своей работы я зафиксировала рост познавательного интереса учащихся к предметам под влиянием межпредметных связей и интегрированного обучения. Интегрированное обучение  стимулирует тягу к знаниям, укрепляет интерес к предмету, расширяет заинтересованность, углубляет знания, способствует становлению интересов профессионального плана, способствует развитию научного стиля мышления учащихся, формирует комплексный подход к учебным предметам; формирует убеждение учащихся, что они могут изучать с пониманием более сложные вещи в сравнении с теми, которые предлагаются в учебнике; приобщает школьников к научно-исследовательской деятельности. Наиболее сложное в проведении интегрированных уроков это их проведение одновременно двумя учителями с несовпадающими уроками в расписании, а также не одновременное прохождение материала объединяющего темы по некоторым предметам. Так же мною и учителем физики Белоусовым Н.В. были проведены интегрированные уроки математика-+физика, математика+ информатика.

Примеры некоторых интегрированных уроков:

 Интегрированный урок в 7 классе

 «Степень на уроках математики и физики»

Подготовили :

 учитель математики :Семендяева Л.В.

учитель физики : Белоусов Н.В

                                    Пояснительная записка

Современное производство, с его высоким уровнем механизации, широкой автоматизацией контроля и управления технологическими процессами, применением электронно-вычислительных машин, все более и более требует от рабочих инженерно-технических знаний, понимания научных принципов производства, высокого уровня развития мышления, творческих способностей. Начинать развивать эти качества нужно в период обучения в школе, когда формируется личность с ее взглядами, убеждениями, знаниями, умениями и способностями. В наших учебных программах, как правило, сохраняется традиционная разобщенность предметов. Поэтому вопрос интеграции привлек наше внимание. Межпредметные связи мы рассматриваем, как дидактическое условие повышения научного уровня знаний учащихся.

В 7-м классе важное значение имеют графические и расчетные задачи, отражающие межпредметные связи физики с математикой. В вычислительных задачах по курсу физики довольно часто используют знания о приближенных вычислениях и решении линейных уравнений, известных из курса математики. Межпредметные связи помогают нам добиться более высокого уровня умения оперировать знаниями, получаемыми на уроках физики и математики, в решении задач комплексного характера, умения осуществлять всесторонний подход к изучению явлений, протекающих в природе и технике.

Велико значение межпредметных связей в развитии мышления и творческих способностей учащихся. Осуществление межпредметных связей приводит к образованию в сознании учащихся межсистемных ассоциаций, а это приводит к серьезным изменениям психологии мышления: мышление становится более гибким, подвижным, что очень важно для решения задач творческого характера.

Цели урока:

Сформировать потребность в знании через показ взаимосвязи между науками и жизнью;     через показ значимости математики как метода (языка) научного познания.

Создать условия для развития интереса к предметам

развивать умение использовать теоретические знания при решении практических  задач.

Способствовать воспитанию аккуратности в вычислительных процессах.

Система оценки:

На протяжении всего урока, за каждое задание учащиеся могут набрать определенное количество баллов. Все набранные баллы заносятся в оценочный лист (приложение 4). Критерии оценивания будут озвучиваться перед каждым заданием. Количество набранных баллов «экипажем», озвучивается в конце каждого задания.

Тип урока: интегрированный урок 

Ход урока:

1.Организационный момент. (1 минута)

Здравствуйте, сегодня мы с вами отправляемся в космическое путешествие по физико-математической галактике. Вы разделены на экипажи и каждому экипажу нужно выбрать командира, который назначает отвечающих на вопросы, обеспечивает своевременную сдачу карточек, следит за дисциплиной в группе.

2.Постановка цели урока. (1 минута)

Сегодня мы продолжим работу над степенями. Повторим свойства степеней, а также покажем применение этих свойств при решении физических задач, вспомним этапы решения задач по физике, перевод единиц в систему СИ.

В ходе урока все набранные баллы будут заноситься в оценочный лист. Критерии оценивания будут озвучиваться перед каждым заданием. Перед вами, на столах находятся листы, на которых вы будете производить все вычисления, но итоговое решение вы должны записать в общую карточку.

3.Актуализация опорных знаний и умений учащихся (работа в группах)

Задание1: Найди ошибку (2 минуты письменно + 2 минуты разбор заданий)

- Ученик, выполняя преобразования выражений, допустил ошибки. Исправьте ошибки и объясните, какие определения, свойства и правила не знает ученик. На данное задание вам отводится 2 минуты. По истечении времени один представитель от группы (1 поднявшая руку группа) объясняет решение всех примеров. Если группа отвечает неправильно, то ход переходит к другой группе.  За каждый правильно решенный пример, группа получает 1 балл.

  5 • 5 • 5 • 5 = 4 ⁵;                     2 ³ • 2 ⁷ = 4 ¹⁰;

                     7¹ = 1;                                     2 ³⁰ : 2 ¹⁰ = 2 ³;

                    4 ⁰ = 4;                                   (2х) ³ = 2х ³;

2     ³ • 2 ⁷ = 2 ²¹;                        (а ³) ² = а ⁵.

Задание 2: Совершенствование интеллектуальных и практических умений учащихся.

(работа по карточкам 4 минуты+ 1 минута разбор)

Решили задание: теперь проверяем ответы на доске, цветными карандашами вы должны аккуратно зачеркнуть неверное решение и сверху подписать правильное. Те, у кого были ошибки поднимают руки и объясняют в чем была ошибка. Ответственный от группы собирает карточки и сдает учителю на проверку.

4. В этом году вы начали изучать новый предмет- физику. И тут вам не обойтись без математики при подсчетах по физическим формулам.

Задание 3: (1 минута)

Давайте вспомним, какие знания нам могут понадобиться при решении задач по физике. С чего мы начинаем решение задачи?

1) Составить Дано по условию задачи

2) Необходимо выразить единицы измерения в системе СИ (система единиц физических величин). Перед тем как решить задачу, вспомним, как мы переводим из одной единицы измерения в другую.  (по группам, задание на экране, группа которая первая дает правильный ответ получает 1 балл)

Слайд №3-4

(2 минуты)

Ø 72 км/ч=20м/с                                   

Ø 120 км/ч=33м/с

А теперь давайте, переведем единицы измерения в систему СИ, а затем приведем к выражению, содержащему степень.

Ø 8 г =... кг (8*10^{-3 кг)}                        

Ø 30кН = …Н (3*10³Н)

    3) Выражение компонентов из формул (2 минуты)

Задание: Выразить компоненты из формул:

Ø ρ=m/V (плотность)

Ø P=m∙g (вес тела)

  Ответ:

Ø m=pV  V=m/p

Ø m=P/g.   g=P/m    (g=9.8 Н/кг)

Итак, мы с вами вспомнили некоторые этапы, которые могут понадобиться при решении физических задач. А теперь давайте решим задачу: (Каждой группе раздается карточка с задачей. На решение задач отводится 3 минуты. В это время у доски оформляет задачу представитель экипажа. По истечении 3-х минут, каждый экипаж сверяет с доской решение задачи и, если есть исправляют ошибки. Оценивается правильное и аккуратное оформление задачи и решение. За правильное решение команда получает 1 балл)

Задача: (3 минуты письменно+ 2 минуты исправление и проверка на доске) приложение 1

№1. Скорость первого искусственного спутника Земли, запущенного в СССР в 1975 г., составляла примерно 28 080 км/ч. Определите путь, пройденный этим спутником за 5 минут. (вызываются по одному участнику от команды, первый – составляет дано, второй – переводит в систему СИ, третий – выражает компонент из нужной формулы и решает задачу)

 Решение:

№2

За какое время солнечный свет достигает Земли, если расстояние от Земли до Солнца составляет примерно 150∙10⁶ км?

№3

К 17 ч 12 сентября 1959 г.  Вторая космическая ракета, доставившая советский вымпел на Луну, удалилась от поверхности Земли на расстояние 101 000 км. К 22 ч того же дня она находилась уже на расстоянии 152 000 км от Земли. Определите среднюю скорость удаления ракеты от Земли.

Молодцы! Без математических навыков вычисления, мы бы не смогли решать задачи по физике.

Задание: (1 минута)

 В следующем задании Вам необходимо разгадать кроссворд, в котором зашифровано имя великого древнегреческого ученого математика и физика, ключевое слово – расположено в столбике по вертикали. Сейчас мы проверим ваши знания, полученные на уроках математики и физики. (На столах находятся карточки с кроссвордом, на разгадывание кроссворда отводится 4 минуты, после этого на экране появляются ответы, учащиеся подсчитывают баллы, максимум 7 баллов). Приложение 2

По горизонтали:

1) Единица времени.

2) Свойство тел сохранять состояние покоя или равномерного прямолинейного движения.

3) Приспособление для преобразования силы.

4) Причина изменения скорости тела.

5) Отрезок в треугольнике, соединяющий вершину треугольника с серединой противолежащей стороной.

6) Выражение, в виде произведения одинаковых множителей, называется….

7) Величина, которая бывает правильной и неправильной.

Сообщение: (3 минуты)

 Мы с вами разгадали имя ученого, а узнать больше об этом ученом нам поможет ____________________________ (рассказывает ученик) Приложение 3

Вывод: Больше информации, об открытиях Архимеда и других ученых, вы узнаете при дальнейшем изучении алгебры, геометрии и физики. Наш урок является своеобразным “мостиком” между предметами математики и физики.

Теперь вы можете посмотреть на физику и математику совсем другими глазами. А теперь скажите почему Физика без математики невозможна?

(Математика при изучении физики вооружает нас математическим аппаратом, который прошел через все этапы нашего урока:

ü Вычисления

ü Перевод единиц

ü Выражение компонентов)

Подведение итогов урока (рефлексия)

Карточки:

А теперь мы попросим поднять желтую карточку тех, кто уже сталкивался в своей жизни с физико-математическими явлениями (с интеграцией физики и математики)

Те, кому из вас захотелось больше узнать о взаимосвязи между математикой и физикой, поднимите зеленую карточку. 

Выставление оценок по «оценочному листу» Приложение 4

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ 1

Решение задач

№1. Скорость первого искусственного спутника Земли, запущенного в СССР в 1975 г., составляла примерно 28 080 км/ч. Определите путь, пройденный этим спутником за 5 минут.

№2

За какое время солнечный свет достигает Земли, если расстояние от Земли до Солнца составляет примерно 150∙10⁶ км? (подсказка: скорость света C ≈ 3• 10⁸ м/

№3

К 17 ч 12 сентября 1959 г.  Вторая космическая ракета, доставившая советский вымпел на Луну, удалилась от поверхности Земли на расстояние 101 000 км. К 22 ч того же дня она находилась уже на расстоянии 152 000 км от Земли. Определите среднюю скорость удаления ракеты от Земли.

ПРИЛОЖЕНИЕ 2

Кроссворд

По горизонтали:

1) Единица времени.

2) Свойство тел сохранять состояние покоя или равномерного прямолинейного движения.

3) Приспособление для преобразования силы ...

4) Причина изменения скорости тела.

5) Отрезок в треугольнике, соединяющий вершину треугольника с серединой противолежащей стороной.

6) Выражение, в виде произведения одинаковых множителей, называется ….

7) Величина, которая бывает правильной и неправильной.

ПРИЛОЖЕНИЕ 3

Сообщение: Архимед

Несомненно, Архимед — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Архимед сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью. Он проживал с 287-212г до нашей эры. Во время службы у царя Герона II, Архимед определил чистоту состава золотого венца царя при помощи найденного им закона выталкивающей силы, тогда он воскликнул «ЭВРИКА», что означало нашел.

Хорошо известен рассказ о жертвенном венце Герона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну, и заметил, что вытесненная его телом вода пролилась через край. Гениального учёного тут же осенила яркая идея, и с криком “Эврика, эврика!” он, как был нагой, бросился проводить эксперимент. Идея Архимеда очень проста. Тело, погружённое в воду, вытесняет столько жидкости, каков объём самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т.е. узнать его объём. А, зная объём и взвесив венец, легко вычислить удельную массу. Это и даст возможность установить истину: ведь золото — очень тяжёлый металл, а более лёгкие примеси, и тем более пустоты, уменьшают удельную массу изделия. Но Архимед на этом не остановился. В труде “О плавающих телах” он сформулировал закон.

Другая легенда рассказывает, что Архимед соорудил систему блоков, с помощью которой один человек смог спустить на воду огромный корабль. Крылатыми стали тогда произнесенные Архимедом слова: «Дайте мне точку опоры, и я поверну Землю»

Его конструкторские способности использовались в военных целях при защите стен города. Огромен вклад Архимеда и в развитие математики. Ученый вычислил отношение длины окружности к диаметру. Используя принцип интегрирования, Архимед открыл число пи. 

ПРИЛОЖЕНИЕ 4

Оценочный лист

Интегрированный урок

по истории и математике в 5 классе

Учителя Лавренюк Н.В., Семендяева Л.В.

ТЕМА.  Финикия.

               Решение задач по теме «Обыкновенные дроби»

ЦЕЛЬ.   История: рассмотреть особенности хозяйственной жизни и общественного строя Финикии, усовершенствовать навыки работы с историческими источниками; умение определять влияние географического расположения и природных условий на развитие государства; воспитывать интерес к изучению истории.

               Математика: систематизировать, обобщить тему «Обыкновенные дроби», показать практическое применение этой темы; развивать умения решать задачи по данной теме; воспитывать интерес к изучению математики

ХОД УРОКА

I.       Организационный момент

II.     Сообщение темы, целей, задач урока

Учитель истории. Ребята, у нас сегодня необычный урок. Я предлагаю вам отправиться в путешествие по Средиземному морю. Отправляясь в путешествие, каждый путешественник собирает багаж с необходимыми ему в дороге вещами. Мы возьмем с собой в дорожный чемодан знания по истории и математике.

III.  Восприятие и осознание нового материала

Но поскольку стран очень много, давайте обратимся в туристическое бюро, которое и поможет выбрать конечную цель нашего путешествия.                   

Туристическое бюро.

(Учащиеся получают предварительное задание подготовить информацию о географическом положении и природно-климатических условиях Финикии).

Первый ученик. (Показывая по карте) Я предлагаю отправиться на восточный берег Средиземного моря, заселенный финикийцами. Область эта называлась Финикия. Она представляла собой полосу между морем и горами шириной до нескольких десятков километров. Географическое положение Финикии было очень выгодным, так как она находилась на перекрестке караванных и морских торговых путей, соединивших разные страны.

Второй ученик. Климат Финикии был благоприятен для развития полевого земледелия и садоводства. Земледельцы выращивали сады и виноградники, делали оливковое масло.

Третий ученик. Ограниченное количество земли ускоряло процесс возникновения городов. Уже в первой половине третьего тысячелетия до н.э. на территории Финикии существовал город - государство Библ. Позднее возникают города по всему восточному побережью Средиземного моря.

Учитель истории. Решено! Мы с вами отправляемся в Финикию. Наш корабль причалил к пристани, и мы сошли на берег. И там наше внимание привлек странный человек, который что-то рассматривал вокруг и записывал. Тогда мы подошли к нему и спросили, чем он занимается.

Ученик. Помогите мне определить в частях количество прибывших в порт кораблей с Крита, потому что я только знаю, что египетских кораблей была ¹/₂ часть от общего количества, Малой Азии -  ¹/₄, а Кипра  - ¹/₇.

Учитель истории. Итак, давайте сделаем вывод, с какими странами торговала по морю Финикия.

(Ответы учащихся).

Учитель истории. Продвигаясь дальше, мы попали на верфь и увидели, как строятся финикийские корабли, которые заметно отличались от остальных. Давайте спросим у работников верфи о том, как они создают такие корабли.

Первый работник верфи. Из кедровых и дубовых досок мастера строят быстроходные корабли. Наряду с торговыми судами на верфях строились и боевые корабли. Финикийские корабли плавали под парусами и на веслах. Гребли рабы, прикованные к скамьям. Во время шторма рабы тонули вместе с кораблями.

Учитель истории. А зачем Финикии такой мощный флот?

Второй работник верфи. Финикийцы нагружали товарами корабли и, следуя вдоль берега, добирались до Египта. Кроме того финикийцы первые на своих кораблях объехали вокруг Африки. Они отправились из Египта по красному морю, а возвратились домой через три года по Средиземному.

Учитель истории. Мы ушли с пристани и оказались в самой оживленной части города. Вы сейчас сами определите, какой.

Сценка «На базаре»

Учитель математики. Ну что ребята! Вы догадались, где мы находимся?

Ученик. На базаре.

Учитель математики. А так как на базаре в процессе торговли возникали всевозможные ситуации, поэтому мы сейчас, объединившись в группы, попробуем разрешить проблемы купцов.

Учитель истории. А, решив задачи, мы сможем определить, с какими странами еще торговали финикийцы, что покупали, а что продавали.

(Класс объединяется в группы для решения задач).

Задача 1.

У купца из Палестины было 50 монет. На закупку вина он истратил 10 ¹/₂  монет, на оливковое масло 7 2/5 монет. Остальное потратил на закупку кедрового дерева. Сколько купец потратил монет на закупку дерева?

Задача 2.

Купец из Сирии продал изысканные одежды на 30 Уг монет, мулов на 40 2/3 монет, а закупил стеклянных сосудов и вина у финикийцев на 25 1/3 монет больше, чем одержал от торговли. На какую сумму купец приобрел товар?

Задача 3.

Купец из Финикии продал пурпурных одежд на 45 ¹/₂  монет, а на вырученные деньги и имеющиеся у него сбережения приобрел рабов на 120 монет. Определить сбережения, которые были у купца.

Задача 4.

У купца из Палестины было 50 монет. На закупку вина он истратил 10 1/2 монет. На оливковое масло 7 2/5 монет. Остальное потратил на закупку кедрового дерева. Сколько потратил на закупку дерева?

Задача 5.

Финикиец на рынке купил у израильских купцов на 3 ¹/₄  имеющихся у него монет пшеницы, а овец 2 ¹/₂  монет больше, чем потратил на пшеницу. На лошадей потратил на три монеты больше, чем на овец и пшеницу вместе. Сколько денег было у финикийского купца.

Учитель истории. Назовите страны, с которыми еще торговала Финикия. Какие товары продавали финикийские купцы, а какие покупали?

Развитие морской торговли привело к расцвету в Финикии искусства, мореплавания. Финикийцы осуществляли плавание не только в Средиземное море, но и выходили в Атлантический океан, достигали берегов современных Англии и Ирландии. Финикийцы во время морские экспедиций основали поселения на побережье Средиземного моря. Такие поселения людей, переселившихся из другой страны, называются колониями. Самой могущественной колонией был Карфаген на северном побережье Африки. Я предлагаю вам мысленно перенестись в Карфаген. Ребята, посмотрите, вот и местный житель. Давайте попросим его рассказать о своем городе.

Местный житель. Дети, если вы отгадаете мою загадку, я с удовольствием расскажу вам о Карфагене.

Задача.

Будет ли в следующих столетиях и тысячелетиях год, цифры которого перевернуть и он будет показывать тот же самый год?(1961,888)

Выступление местного жителя о Карфагене.

Учитель истории. Ребята, вот мы с вами и закончили наше путешествие, но совершая это путешествие мы не смогли обойтись без математики, ее чудесными дробями.

Учитель математики. А ведь у математики есть своя история. Так давайте поговорим об истории возникновения дробей и о математиках, которые относятся к истории Финикии.

Ученики рассказывают о Фалесе, древнегреческом философе и математике, относившемся к знатному финикийскому роду, и о происхождении дробей.

IV.  Осмысление и систематизация

Учитель истории. В какой стране мы с вами побывали? 

Упражнение «Снежный ком». Каждый ученик говорит по одному предложению из выученной темы.

Учитель математики.  Какие задачи вы решали.  Для чего необходимы были дроби в древние времена?

V.    Подведение итогов

Учитель истории, учитель математики подводят итоги урока с выставлением оценок.

VI.  Домашнее задание

VII.            История: выучить  § 15, отвечать на вопросы в конце §

VIII.         Математика: