Оглавление

Оригаметрия – очень молодая область, и пока не существует соответствующих программ и учебников, которые давали бы подобный материал. Вместе с тем многие понятия курса геометрии в школе гораздо проще и нагляднее объясняются с помощью оригаметрии.

Для построения теории используется система аксиом. 

Аксиома 1: Существует единственный сгиб, проходящий через две данные точки

Аксиома 2: Существует единственный сгиб, совмещающий две данные точки

Аксиома 3: Существует единственный сгиб, совмещающий две данные прямые

Аксиома 4: Существует единственный сгиб, проходящий через данную точку и перпендикулярный данной прямой

Аксиома 5: Существует единственный сгиб, проходящий через данную точку и помещающий другую данную точку на данную прямую Аксиома 6: Существует единственный сгиб, помещающий каждую из двух данных точек на одну из двух данных пересекающихся прямых Аксиома 7: Для двух данных прямых и точки существует линия сгиба, перпендикулярная первой и помещающая данную точку на вторую прямую.

Задача 1. Разделить отрезок на две равные части.

Решение: Для того, чтобы разделить отрезок на две равные части, необходимо совместить две противоположные стороны квадрата.

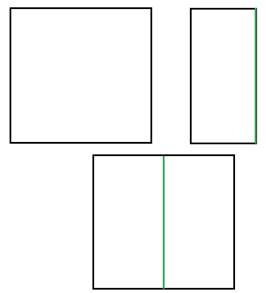
Задача 2. Из данного квадрата получите квадрат, площадь которого в 4 раза меньше площади данного.

Решение: Сложить квадрат пополам 2 раза.

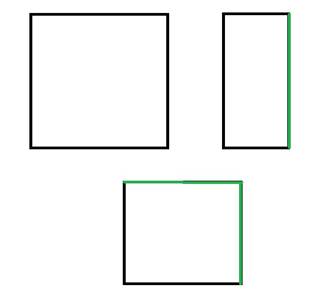
Задача 3. Постройте центр окружности.

Решение: Круглый лист согнуть пополам два раза, точка пересечения линий сгиба и будет центром.

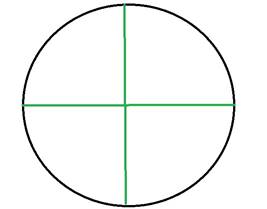
Задача 4. Отрезок длиной х разделён произвольно на две части. Найти расстояние между серединами этих частей. 

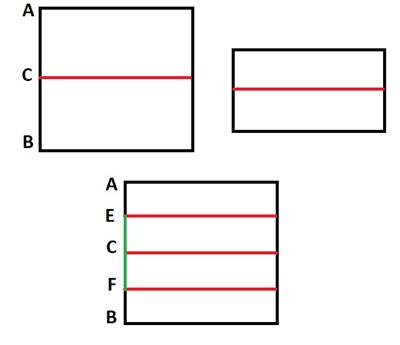
Решение: Возьмём лист бумаги. Край – отрезок АВ. Согнём лист пополам и отметим полученную точку на отрезке АВ буквой С. Согнём лист так, чтобы точки В и С совместились и отметим точку E – середину отрезка ВС. Аналогично найдём середину АС и отметим точкой F. Получили бумагу, сложенную в 2 равных слоя, EF (отмечен зелёным) это половина листа, то есть х/2.

5.        На сколько частей делят плоскость: 

а) Две пересекающиеся прямые

б) Три прямые, пересекающиеся в одной точке 

в) Три прямые, пересекающиеся в двух точках 

г) Три прямые, пересекающиеся в трёх точках 

Решение: за плоскость принимаем любой лист бумаги. Сгибаем его так, что бы прямые удовлетворяли условиям

А)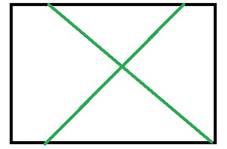Ответ: на 4 части

Б)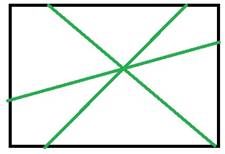Ответ: на 6 частей

В)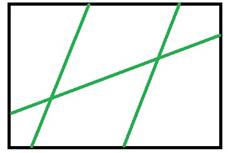Ответ: на 6 частей

Г)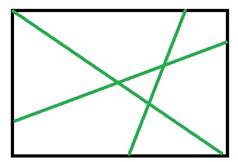Ответ: на 7 частей

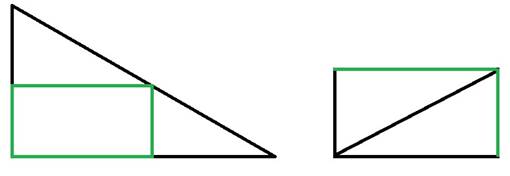
6.        Докажите, что сумма острых углов прямоугольного

треугольника равна 90°. 

Решение: Складываем по красным линиям, получится прямоугольник, один из углов которого образуют острые углы данного треугольника.

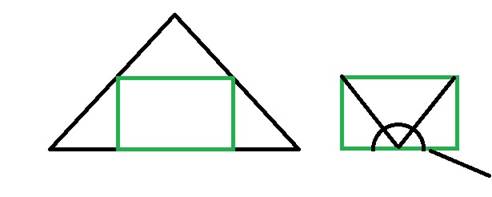
Задача 7. Докажите, что сумма углов треугольника 180° 

Решение: После сгибания треугольника по зелёным линиям, его углы образуют развёрнутый угол.

180°

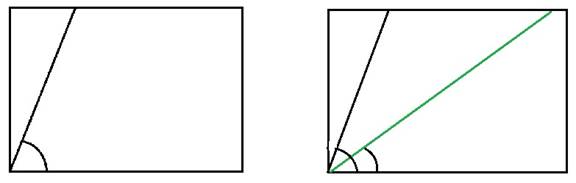
Задача 8. Построить биссектрису данного угла. 

Решение: Чтобы построить биссектрису угла нужно начертить на листе бумаги любой угол а и сложить этот угол пополам.

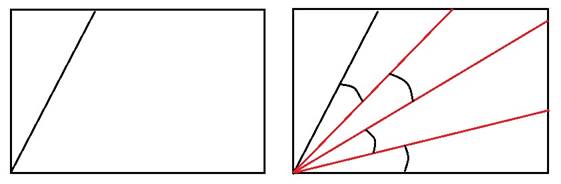
9. Разделить угол на четыре равные части. 

Решение: Сложить данный угол пополам два раза.

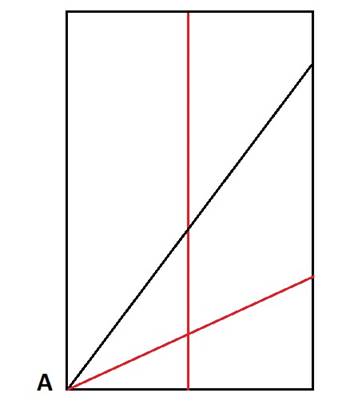
Задача 10. Разделить прямой угол на три равные части. 

Решение: Возьмём прямоугольный лист бумаги отметим угол, который будем делить, буквой А и сложим лист пополам. Теперь совместим правый нижний угол с полученной прямой и получим точку В. Если разогнуть лист, то мы увидим, что угол А разделился на три равные части прямой АВ и линией сгиба.