Основи гідродинаміки потоків

2.3. Основи гідродинаміки потоків.

     2.3.1. Основні характеристики потоку.

     Витрата рідини й швидкість руху. Переміщення рідин по трубопроводах, каналах, апаратах відбувається внаслідок перепаду тиску, який може виникнути за рахунок різниці рівнів чи густини рідини в різних точках середовища або створюється роботою спеціальних машин – насосів, компресорів і т.ін. Об'єм рідини, що протікає через який-небудь переріз потоку в одиницю часу, називають об'ємною витратою рідини Q.

Як було показано вище (рис.2.1), внаслідок впливу сил в'язкості (тертя) у різних точках поперечного перерізу потоку, швидкість часток рідини неоднакова: по осі потоку вона максимальна, а біля стінки трубопроводу дорівнює нулю. Оскільки встановити розподіл швидкостей по поперечному перерізу потоку часто важко, в інженерних розрахунках звичайно використовують так звану середню швидкість, при цьому допускають, що всі частки потоку рухаються з однаковою швидкістю. Така умовна швидкість w визначається відношенням об'ємної витрати рідини Q до площі перетину потоку S:

.                                                    (2.19)

Тоді об'ємна витрата рідини Q (м³/c, м³/год) і її масова витрата М (кг/с, кг/год) визначаються відповідно рівняннями

                                     (2.19a)

де ρ – густина рідини, кг/м³. Величина ρw (кг/(м²·с)) представляє собою масову швидкість рідини. Рівняння (2.19) і (2.19а) називають рівняннями витрати й широко використовують у розрахунках трубопроводів і хімічних апаратів.

      Види руху. Субстанціональна похідна. Як відзначалося в розділі 1, залежно від зміни параметрів процеси підрозділяють на стаціонарні (сталі) і нестаціонарні (несталі). При сталому русі рідини ∂w/∂τ=, швидкість не залежить від часу, і течія у будь-якому місці потоку залишається незмінною, тобто швидкість є функцією тільки просторової системи координат При несталому русі ∂w/∂τ, і швидкість змінюється не тільки в просторі, але й у часі. У цьому випадку . Як приклад несталого руху можна привести витікання рідини з отвору в посудині: без подачі в посудину рідини рівень у ньому знижується, при цьому швидкість витікання рідини зменшується в часі.

      Зміна параметрів рідини в часі і в просторі описується в гідродинаміці повною або субстанціональною похідною, за змістом – похідною, що прямує за потоком.

Нехай u – будь-який параметр, що змінюється в потоці рідини як в часі, так і в просторі (наприклад, густина, температура, тиск, концентрація рідини або складові її швидкості w в напрямку осей координат  - w_x, w_y і w_z). Зміна параметра u за одиницю часу в фіксованій точці простору А ( виражається частинною похідною ∂u/∂τ, а зміна u в цій точці за нескінченно малий проміжок часу dτ складає Ця величина є місцевою або локальною зміною даної величини, яка при сталому русі дорівнює нулю. Однак за час dτ частка рідини  переміщується з точки А з координатами x, y і z в точку В з координатами (x+dx), (y+dy) та (z+dz). Внаслідок такого переміщення зміни величини u, що відповідають проекціям шляху dx, dy і dz, дорівнюють  Таким чином, якщо рух частки рідини є сталим (локальна зміна u дорівнює нулю), то при переміщенні частки з А в В зміна параметра u виражається сумою вищеозначених компонент:

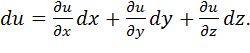
Цей вираз характеризує конвективну зміну параметра u.

     В умовах несталого руху [u=f(x,y,z,τ)], внаслідок зміни u в часі в кожній точці простору за час dτ, значення зазначеного параметра також зміниться на  Відповідно, повна зміна u при несталому русі є сумою локальної та конвективної змін:

звідки

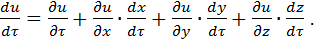
     Однак

де  - складові швидкості вздовж відповідних осей координат, на які можна розкласти швидкість w.

     Після відповідної підстановки маємо:

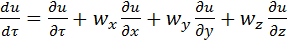                           (2.20)

     У випадку сталого процесу  ():

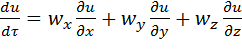                                 (2.21)

     Рівняння (2.20) та (2.21) представляють собою субстанціональну похідну параметра u відповідно для несталого та сталого процесів. Субстанціональна похідна характеризує зміну якого-небудь параметра або властивості матерії (субстанції) в часі при переміщенні матеріальних часток в просторі.

     При русі частки рідини зі швидкістю w конвективну та локальну зміну зазнають всі складові швидкості вздовж осей координат  (надалі – w_i).

Вираження субстанціональної похідної відносно складових швидкості потоку рідини при несталому режимі має вигляд:

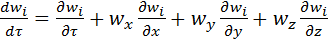                       (2.22)

У цьому випадку похідні  (де i=x,y,z) характеризують складові прискорення потоку рідини вздовж відповідних осей координат, при цьому складова  представляє собою локальне прискорення, а складова ( ) – конвективне прискорення.

        Режими руху реальної рідини. Рядом дослідників (Хагеном - у 1869 р., Менделєєвим - у 1880 р., Рейнольдсом - у 1883 р.) було помічено, що існує два принципово різних режими руху рідини. Найбільш повно це питання було досліджено Рейнольдсом за допомогою надзвичайно простої дослідної установки.

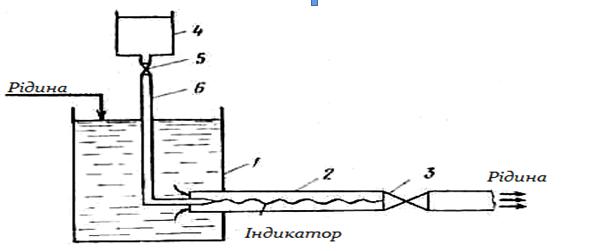
Рис. 2-7. Установка Рейнольдса для вивчення режимів руху рідини:

1 - посудина; 2 - скляна труба; 3, 5 - крани; 4 – ємність з індикатором; 6 - капілярна трубка

       Установка (рис.2.7) складалася з посудини 1, у якій для створення стаціонарного потоку підтримувався постійний рівень рідини, і приєднаної до неї скляної горизонтальної труби 2. На початку досліду злегка відкривали кран 3, і з посудини починала текти робоча (досліджувана) рідина. Потім у трубу 2 по її осі через капілярну трубку 6 з ємності 4 за допомогою крана 5 подавали підфарбований струмінь рідини (індикатор), що мав однакові з робочою рідиною густину і швидкість. При малих витратах робочої рідини тонкий пофарбований струмінь просувався усередині труби, не змішуючись із усією масою рідини, тобто шляхи часток робочої й підфарбованої рідини в цих умовах прямолінійні й рухаються вони по паралельних траєкторіях. Таким чином, підфарбований струмінь рухається уздовж осі труби незбуреним (якщо не вважати молекулярної дифузії барвника). Така стала течія була названа паралельно-струменистою, або ламінарною, тому що деформація рідини при цьому аналогічна деформації тонких пластин (шарів) у пачці, що ковзають одна по іншій.

При досить великих витратах (швидкостях) рідини характер течії пофарбованого струменя зовсім інший. Спочатку струмінь проходить деяку відстань у трубі 2, залишаючись незбуреним, а потім він починає набувати хвилеподібного руху, коливається зі сторони в сторону і, нарешті, повністю розмивається, змішуючись із основною масою робочої рідини. Цей неупорядкований рух з інтенсивним перемішуванням по перетину потоку було визначено Рейнольдсом як хвилястий; зараз його прийнято називати турбулентним.

Експериментально було встановлено, що перехід від ламінарного режиму до турбулентного залежить не тільки від швидкості потоку w, але й від фізичних властивостей рідини (в'язкості µ, густини ρ) і визначального геометричного розміру - діаметра труби d: потік стає більш інтенсивним зі збільшенням w, d і ρ та зменшенням µ. Безрозмірний комплекс wdρ/μ, у який входять перераховані величини, дозволяє за його числовим значенням судити про режим руху рідини. Цей комплекс називають числом (критерієм) Рейнольдса й позначають Rе:

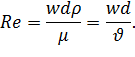
Значення числа Рейнольдса для умов переходу від ламінарного режиму руху рідини до турбулентного називають критичним. При русі рідин по прямих гладких трубах Rе_кр = 2300. При Rе < 2300 режим руху рідини буде ламінарним, а при Rе > 2300 - турбулентним. Однак при 2300<Rе<10000 режим руху рідини нестійкий - рух може бути і ламінарним, і турбулентним; цю область значень Rе часто називають перехідною. Тому вважають, що стійкий (розвинений) турбулентний режим при русі рідин по прямих гладких трубах установлюється при Rе >10000.

У випадку, якщо потік збурюється на своєму шляху (шорсткуваті стінки труби, звуження або розширення потоку й ін.), критичне значення Rе_кр може істотно знижуватися. Це тим більше відноситься до течій потоків у хімічних апаратах, що мають звичайно складну конфігурацію. У цих випадках експериментально визначають значення Rе_кр, які для типових апаратів наведені в довідковій літературі. Відзначимо, що критичне значення Rе_кр зменшується також за умов неізотермічного потоку через виникнення конвекційних струменів рідини в напрямку, перпендикулярному осі потоку.

У випадку, якщо рідина рухається по каналу (трубопроводу, апарату) складної конфігурації, при розрахунку Rе замість d використовують поняття гідравлічного радіусу r_г або еквівалентного діаметру d_е.

Під гідравлічним радіусом r_г розуміють відношення площі перерізу S потоку до змоченого периметра П каналу (трубопроводу): r_г=S/П.

Для круглої труби

Діаметр, виражений через гідравлічний радіус, називають еквівалентним:

.

Тоді

     Основні характеристики турбулентного потоку. Промислові процеси найбільш часто здійснюються при турбулентному режимі руху потоків, оскільки в цих умовах більшість хіміко-технологічних процесів протікає значно інтенсивніше. Структура турбулентного потоку визначається швидкістю руху потоку, фізичними властивостями рідини, формою й розмірами стінок каналу, обмежуючого потік, й ін.

Окремі елементи турбулентного потоку - вихори здійснюють хаотичні несталі рухи. Під вихором розуміють групу часток, що обертаються навколо однієї миттєвої осі з однаковою кутовою швидкістю, так що стосовно навколишньої рідини вихор подібний до твердого тіла. У процесі турбулентної течії вихори безупинно виникають і розпадаються. Розмір таких вихорів, або глибина їхнього проникнення до руйнування, залежить від ступеня розвитку турбулентності в потоці, або її масштабу, і тому називається масштабом турбулентності. Масштаб турбулентності багато в чому визначається зовнішніми умовами течії (наприклад, діаметром трубопроводу або каналу). Турбулентність, не обмежену впливом стінок, називають вільною (наприклад, витікання рідких і газових струменів у нерухливу рідину).

Вихори пульсують щодо їхнього середнього положення в потоці рідині; такий рух називають пульсаційним. Аналогічно пульсує й миттєва швидкість у даній точці потоку. Безладне переміщення вихорів приводить до інтенсивного перемішування рідини по перерізу потоку.

     Через те, що маса вихору й шлях, що він проходить, незрівнянно більше маси молекули й довжини її вільного пробігу, перенос імпульсу, маси й теплоти за рахунок хаотичного руху вихорів значно перевищує молекулярний перенос, викликаний тепловим рухом молекул.

      При турбулентному русі крива розподілу швидкостей по перетину (профіль швидкості) має вид, відмінний від параболи (характерної для ламінарного руху) - вершина кривої значно згладжена (рис. 2.8). При цьому відношення =. Чим більше число Rе, тим більше відношення , тобто тим ближче середня швидкість потоку до максимальної (на осі потоку).

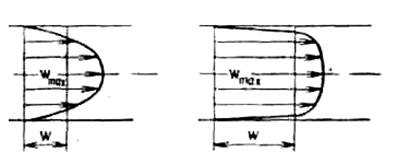
                                            а)                                       б)   

Рис. 2.8. Розподіл швидкостей по перерізу потоку при ламінарному (а) і турбулентному (б) режимах руху

Теоретично описати профіль швидкостей у цьому випадку надзвичайно важко через складний характер турбулентного руху. Тому криві на рис. 2.9 виражають розподіл не дійсних, а осереднених у часі швидкостей, тобто турбулентна течія, строго говорячи, по суті не є сталою - миттєві швидкості в кожній точці потоку змінюються в часі. Але використання осереднених у часі швидкостей дозволяє приблизно розглядати цей рух як сталий. Таким чином, турбулентний рух можна характеризувати як квазістаціонарний (умовно сталий).

Різницю між дійсною й осередненою швидкостями  називають миттєвою пульсаційною швидкістю. Оскільки безладний рух вихорів аналогічний тепловому руху молекул газу, опис процесів переносу маси, енергії й імпульсу в турбулентному потоці проводиться методами, аналогічними прийнятим у молекулярно-кінетичній теорії газів. Таким чином, за аналогією з довжиною вільного пробігу молекули вводиться поняття шляху перемішування - відстані, на якому вихор рухається без змішування з навколишньою рідиною. За аналогією з молекулярним переносом кількості руху, що виражається законом внутрішнього тертя Ньютона [рівняння (2.10)], величину напруження турбулентного тертя (або рівну їй густину потоку імпульсу, що переноситься вихорами) приймають пропорційною градієнту швидкості або градієнту, імпульсу:

 .

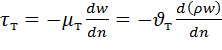Величину  називають коефіцієнтом турбулентної в'язкості; на відміну від молекулярної в'язкості μ вона залежить від усіх параметрів, що характеризують турбулентність, у тому числі від осередненої швидкості. Через те, що маса молекул незрівнянно менше маси вихорів, переміщуваний ними імпульс між сусідніми шарами рідини і їхнє взаємне прискорення й гальмування значно більше і, отже, створюване напруження турбулентного тертя значно вище. У результаті середня турбулентна в'язкість потоку значно перевищує молекулярну (ньютонівську) в'язкість, тобто

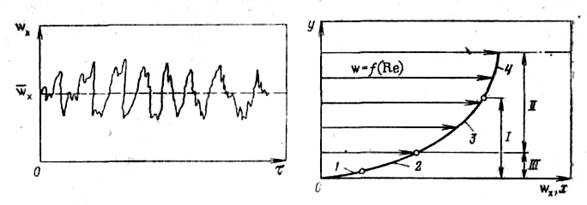Рис. 2.9. Дійсна w_x та осереднена  локальні швидкості рідини в турбулентному потоці.

Рис. 2.10 Модель структури поперечного перерізу турбулентного потоку

1 – в’язкий підшар; 2 - перехідний (буферний) підшар; 3 - турбулентний підшар; 4 - турбулентне ядро потоку. I – пограничний (межовий) шар; II - турбулентна течія; III - область в’язкої течії (масштаб пристінних областей збільшений).

Сумарне дотичне напруження в потоці визначається, відповідно, як молекулярною в’язкістю рідини, так і турбулентністю потоку:

.

Турбулентний потік умовно підрозділяють на ядро й пограничний (межовий) шар, у якому відбувається перехід турбулентного руху в ламінарний, причому швидкість руху по перерізу потоку змінюється від максимальної - по осі потоку до нуля - у стінки каналу.

Графік профілю швидкості (рис. 2.10) дозволяє виявити кілька областей, на які можна розділити течію у каналі. У розглянутому окремому випадку течії в круглій трубі основні зміни швидкості відбуваються в області, що займає менше 15% радіуса труби (потоку). Розмір області, що безпосередньо прилягає до стінки, на малюнку даний у збільшеному масштабі. У дійсності ж товщина областей (I) і (II) становить лише дуже малу частину радіуса - порядку 1% і менше. Незважаючи на малу товщину, ці внутрішні шари істотно впливають на весь потік, тому що значна частка зміни швидкості відбувається саме в них. При цьому різко міняються умови протікання багатьох хіміко-технологічних процесів, оскільки високошвидкісний макроскопічний перенос субстанції в ядрі турбулентного потоку (через інтенсивне перемішування часток рідини по перерізу потоку за рахунок турбулентних пульсацій) поступається місцем, як правило, повільному молекулярному переносу в пристінних шарах. На рис. 2.10 стінка труби схематично зображена гладкою, у дійсності ж поверхня звичайно має нерівності (шорсткість), висота яких порівнянна з товщиною внутрішніх шарів. Ця обставина значно впливає на витрату енергії для створення необхідної швидкості руху потоку.

Розглянемо докладніше області, показані на рис. 2.10.

1.            В’язкий підшар: зміна середньої швидкості визначається значенням коефіцієнта молекулярної в'язкості й практично лінійна, як у ламінарному потоці; при цьому .

2.            Перехідний (буферний) підшар: в’язкі й турбулентні напруження порівнянні по величині, тобто ; відбувається різке загасання турбулентності.

3.            Турбулентний підшар: на течію ще впливає ефект стінки, однак турбулентність розвинена вже в такій степені, що в’язкими напруженнями можна знехтувати, тобто  (оскільки зміна середньої швидкості в цій області практично підкоряється логарифмічному закону, область часто називають логарифмічним шаром).

4.      Турбулентне ядро: потік повністю турбулентний; масштаб турбулентності обумовлений визначальним параметром каналу (діаметром труби).

Ці чотири області можна об'єднати в такий спосіб. Області 1 і 2 становлять в’язкий шар - область в’язкої течії (III), тобто область, у якій в'язкість відіграє значну роль у виникненні тертя й у процесах переносу маси та енергії. В’язкий шар такого виду існує тільки тоді, коли виступи шорсткості стінки малі порівняно з товщиною цього шару. Практично цей опис вірний в тому випадку, коли виступи шорсткості не проникають у перехідний шар. Області 3 і 4 утворять область турбулентної течії (II). У цій області масштаб турбулентності не залежить від в'язкості.

Області 1, 2 і 3 утворюють гідродинамічний пограничний (межовий) шар - пристінну область (I), у якій відбувається перехід турбулентного руху в ламінарний.

Слід зазначити, що розглянута чотиришарова модель турбулентного потоку є значною мірою ідеалізацією реальної течії, оскільки в дійсності границі між шарами розмиті, і виділені на рис. 2.10 точки, що розмежовують ці шари, носять умовний характер.

Тут були розглянуті лише деякі характеристики турбулентного потоку, необхідні в основному для висновків і аналізу рівнянь переносу субстанцій, що будуть розглянуті нижче.

       2.3.2. Рівняння нерозривності (суцільності) потоку.

Установимо загальну залежність між швидкостями в потоці рідини, для якої дотримується умова суцільності, або нерозривності руху, тобто не утворюється порожнеч, незаповнених рідиною.

Виділимо усередині потоку елементарний паралелепіпед об’ємом dV=dxdydz, ребра якого орієнтовані паралельно осям координат (рис.2.11).

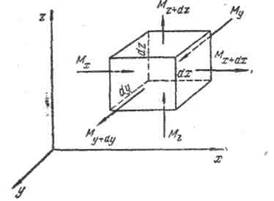
Рис. 2.11. До виводу диференціального рівняння нерозривності потоку.

Нехай складова швидкості потоку уздовж осі х у точках, що лежать на лівій грані паралелепіпеда площею dS=dydz, дорівнює w_x.

     Тоді, відповідно до рівняння (2.19а), через цю грань у паралелепіпед увійде уздовж осі х за одиницю часу маса рідини ρw_xdydz, а за проміжок часу dτ  - маса рідини

де ρ — густина рідини на лівій грані паралелепіпеда.

     На протилежній (правій) грані паралелепіпеда швидкість і густина рідини можуть відрізнятися від відповідних величин на лівій грані й будуть дорівнювати 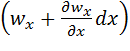 і 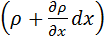, тобто масова швидкість зміниться від ρw_x до 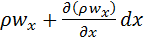. Тоді через праву грань паралелепіпеда за той же час   вийде маса рідини

.

Збільшення маси рідини в паралелепіпеді уздовж осі х

.

Якщо складові швидкості уздовж осей у и z відповідно w_y і w_z, то збільшення маси в елементарному об’ємі уздовж цих осей за аналогією складуть:

,  .

Загальне нагромадження маси рідини в паралелепіпеді за час dτ дорівнює сумі її збільшень уздовж усіх осей координат:

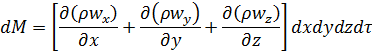
       Разом з тим, зміна маси в повністю заповненому рідиною об’ємі паралелепіпеда можлива тільки внаслідок зміни густини рідини в цьому об’ємі, тобто

Прирівнюючи обидва вищезазначені вираження dM, скорочуючи на dxdydz й переносячи в ліву частину рівняння, остаточно одержимо

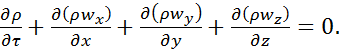                       (2.23)

      Рівняння (2.23) являє собою диференціальне рівняння нерозривності потоку для несталого руху рідини.

      У сталому потоці густина не змінюється в часі, тобто , і рівняння (2.23) приймає вид

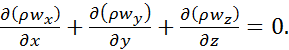                              (2.24)

Для краплинних рідин, які практично нестисливі, а також для газів в умовах ізотермічного потоку при швидкостях, значно менших швидкості звуку, ρ=const і, отже

                                       (2.25)

Рівняння (2.25) є диференціальним рівнянням нерозривності потоку для нестисливої рідини.

       Сума змін швидкості уздовж осей координат у лівій частині рівняння (2.25) називається дивергенцією вектора швидкості й позначається через div w. Тому дане рівняння можна представити як

                                                 (2.25а)

       Для того щоб перейти від елементарного об’єму до всього об’єму рідини, що рухається суцільним потоком (без розривів і порожнеч) по трубопроводу змінного перерізу (рис. 2.12), інтегруємо диференціальне рівняння (2.24). Якби площа перетину трубопроводу не змінювалася, то для сталого односпрямованого руху (у напрямку осі х) інтегрування рівняння (2.24) дало б залежність ρw=const де w - середня швидкість рідини. Якщо ж площа перерізу S трубопроводу змінна, тo, інтегруючи також по площі, одержимо

                                               (2.26)

Для трьох різних перерізів (1-1, 2-2 і 3-3) трубопроводу, зображеного на рис.2.12, маємо

          (2.26a)

де М=ρwS — масова витрата рідини, кг/сек.

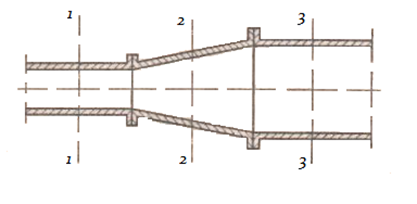
Рис.2.12.До виводу рівняння сталості витрати

Вираження (2.26) являє собою рівняння нерозривності (суцільності) потоку в його інтегральній формі для усталеного руху. Це рівняння називається  також рівнянням сталості витрати.

Відповідно до рівняння сталості витрати, при усталеному русі рідини, що повністю заповнює трубопровід, через кожний його поперечний переріз проходить в одиницю часу однакова маса рідини.

    Для краплинних рідин , і рівняння (2.26) приймає вид

          (2.27)

де  - об'ємна витрата рідини, м³/сек.

З рівняння (2.27) витікає, що швидкості краплинної рідини в різних поперечних перерізах трубопроводу обернено пропорційні площам цих перерізів.

Відповідно до рівняння (2.26), масова витрата рідини через початковий переріз трубопроводу дорівнює її витраті через кінцевий переріз трубопроводу. Таким чином, рівняння сталості витрати є окремим випадком закону збереження маси й виражає матеріальний баланс потоку.

У деяких випадках, наприклад при скипанні рідини внаслідок різкого зниження тиску, утвориться пара, що може привести до розриву потоку. У таких умовах, що спостерігаються іноді при роботі насосів, рівняння нерозривності потоку не виконується.

   2.3.3. Диференціальні рівняння руху ідеальної рідини Ейлера.

Розглянемо сталий потік ідеальної рідини. Як уже відзначалося, вона не має в'язкості, тобто рухається без тертя.

Як і при виводі диференціальних рівнянь рівноваги Ейлера, виділимо в потоці елементарний паралелепіпед об’ємом , орієнтований щодо осей координат (див. рис. 2.3).

Вище було показано (див. 2.2.1), що проекції на осі координат сил ваги й тиску, що діють на паралелепіпед, становлять:

для осі х

,

для осі y

для осі z

       Відповідно до основного принципу динаміки, сума проекцій сил, що діють на елементарний об’єм рідини, що рухається, дорівнює добутку маси рідини на її прискорення.

Маса рідини в об’ємі паралелепіпеда

.

     Якщо рідина рухається зі швидкістю w, то її прискорення дорівнює , а проекції прискорення на осі координат відповідно:  де ,  і  - складові швидкості уздовж осей  х, у і z.

У відповідності з основним принципом динаміки

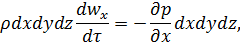
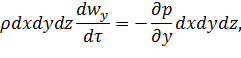
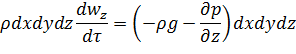
або після скорочення

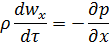
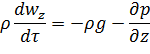
де, відповідно до рівняння (2.22), субстанціональні похідні відповідних складових швидкості дорівнюють (за умови для сталого потоку )

,

,                                      (2.29)

.

Система рівнянь (2.28) з урахуванням (2.29) являє собою диференціальні рівняння руху ідеальної рідини Ейлера для сталого потоку.

При несталому русі швидкість рідини змінюється не тільки при переміщенні частки потоку з однієї точки простору в іншу, але й із часом у кожній точці. Тому, відповідно до рівняння (2.22), прискорення в рівнянні (2.28), які виражаються субстанціональними похідними для несталих умов, мають вигляд:

,

 ,                   (2.30)

.

     Система рівнянь (2.28) з урахуванням виражень (2.30) являє собою диференціальні рівняння руху ідеальної рідини Ейлера для несталого потоку.

2.3.4. Рівняння Бернуллі.

Інтегралом рівнянь руху Ейлера для сталого потоку є рівняння Бернуллі, яке широко використовується для рішення багатьох технічних задач. Наприклад, за допомогою цих рівнянь легко встановити зв’язок між швидкістю, тиском та густиною в живому перерізі усталеного потоку ідеальної рідини, що знаходиться під дією тільки сили тяжіння.

Помножимо ліві та праві частини рівнянь (2.28) відповідно на dx, dy і dz та поділимо на густину рідини ρ:

,

,

.

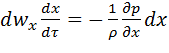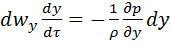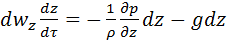     Після складання лівих та правих частин цих рівнянь, враховуючи, що похідні є проекціями швидкості на відповідні осі координат , отримаємо

.

      При сталому русі і тому  – є повним диференціалом гідростатичного тиску. Крім того, враховуючи, що 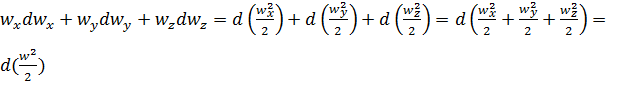, отримаємо рівняння

.

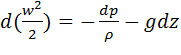Поділимо обидві частини цього рівняння на g=const і перенесемо всі його члени в ліву частину

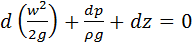
Оскільки для нестисливої рідини ρ=const, суму диференціалів можна замінити диференціалом суми:

 ,

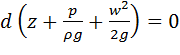звідки після інтегрування

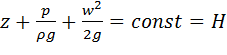                              (2.31)

     Рівняння (2.31) називають рівнянням Бернуллі для ідеальної рідини, а величину  - повним гідродинамічним напором.

     Таким чином, згідно рівняння Бернуллі, для всіх поперечних перерізів усталеного потоку ідеальної рідини значення гідродинамічного напору залишається сталим, тобто

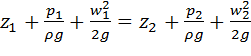                               (2.32)

     Гідродинамічний напір включає три складових, два перших з них входили в основне рівняння гідростатики (2.17): z – нівелірна висота або геометричний напір (h_г) представляє собою питому потенціальну енергію положення в даній точці (даному перерізі);  – напір тиску або п’єзометричний напір (h_п), який дорівнює тиску стовпа рідини над даним рівнем (в даному перерізі потоку), він характеризує питому потенціальну енергію тиску в даній точці (перерізі).

     Таким чином, сума  характеризує повну питому потенціальну енергію в даній точці (перерізі), її називають повним гідростатичним або просто гідростатичним напором (h_ст). Третя складова рівняння (2.31) -   представляє собою швидкісний або динамічний напір (h_д) і характеризує питому кінетичну енергію в даній точці (даному перерізі).

     Складові повного гідродинамічного напору можуть бути виражені як в одиницях довжини , так і в одиницях питомої енергії, тобто енергії, що приходиться на одиницю ваги рідини - .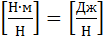

     Згідно рівнянню Бернуллі, для любого перерізу або точки потоку при усталеному русі ідеальної рідини сума потенціальної і кінетичної  енергії рідини залишається величиною сталою. Таким чином, рівняння Бернуллі виражає собою частинний випадок закону збереження енергії (або енергетичний баланс потоку).

     При зміні поперечного перетину трубопроводу і відповідно швидкості руху рідини відбувається перетворення енергії: при звуженні трубопроводу частина потенціальної енергії тиску переходить в кінетичну і, навпаки, при розширенні трубопроводу частина кінетичної енергії переходить в потенціальну, але загальна кількість енергії залишається сталою. Звідси витікає, що для ідеальної рідини кількість енергії, яка поступає з потоком через початковий переріз трубопроводу, дорівнює кількості енергії, що виходить з потоком через кінцевий його переріз.

     Якщо помножити ліву і праву частини рівняння (2.32) на питому вагу рідини , то рівняння Бернуллі для ідеальної рідини може бути представлене наступним чином:

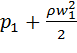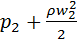+=+                           (2.33)

     У рівнянні (2.33) кожний член представлений у одиницях тиску  і виражає питому енергію, віднесену не до одиниці ваги, а до одиниці об’єму рідини: .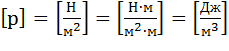

     При русі реальної рідини (на відміну від ідеальної) її гідродинамічний напір Н не залишається сталим, оскільки частки рідини зустрічають опір, викликаний силами в’язкості та різними перешкодами (кранами, вентилями, поворотами, звуженнями та розширеннями і т.ін.), які приводять до зміни перерізу або напрямку потоку. На подолання цього опору, який прийнято називати гідравлічним опором, витрачається енергія рухомої рідини, яка перетворюється на тепло. Це тепло йде на нагрівання потоку і розсіюється в навколишнє середовище. Тому в кожному наступному перерізі потоку енергія частки буде менше, ніж у попередньому, тобто

+>+ .

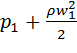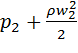При цьому частина потенціальної енергії переходить у втрачений напір. Тому для дотримання балансу енергії при русі реальної рідини в праву частину рівняння (2.33) необхідно ввести член, що враховує втрати напору:

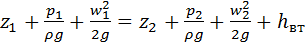                        (2.34)

     Втрачений напір (h_вт) характеризує питому (тобто віднесену до одиниці ваги рідини) енергію, що витрачається на подолання гідравлічного опору при русі реальної рідини.

     Втрачений напір включає дві складові – втрату напору на тертя по довжині трубопроводу (h_т) і на подолання так званих місцевих опорів (h_м.о.), під якими розуміють джерело зміни напрямку або перерізу потоку (повороти, звуження, розширення, вентилі, крани, діафрагми і т. ін..), тобто

     Рівняння (2.34) може бути представлене в іншому вигляді, якщо помножити обидві його частини на ρg:

                    (2.34а)

де  - втрачений тиск.

     За допомогою рівняння Бернуллі можна визначити напір (або тиск) необхідний для того, щоб рідина з заданою швидкістю транспортувалась по даному каналу (трубопроводу), а також швидкість і витрату рідини, час витоку рідини із отвору в резервуарі і т.ін.

     2.3.5. Диференціальні рівняння руху реальної рідини Нав’є – Стокса.

При русі реальної (в'язкої) рідини в потоці рідини крім сил тиску й ваги діють також сили тертя.

Дія сил тертя Т на виділений у потоці в’язкої рідини елементарний паралелепіпед (рис. 2.13) проявляється у виникненні на його поверхні дотичних напружень τ. Розглянемо спочатку відносно простий випадок одномірного  плоского потоку краплинної рідини в напрямку осі х, коли проекція швидкості w_x залежить тільки від відстані z до горизонтальної площини відліку.

     У цих умовах дотичні напруження виникають лише на поверхнях dS=dxdy верхньої й нижньої граней

     елементарного паралелепіпеда. Якщо дотичне              напруження на нижній грані паралелепіпеда дорівнює τ,

то на верхній воно буде становити . Похідна  виражає зміну дотичного напруження уздовж осі z у точках, що лежать на нижній грані паралелепіпеда, а величина  являє собою зміну цього напруження уздовж всієї довжини dz ребра паралелепіпеда.

Зазначені на рис. 2.13 стрілками напрямки сил тертя, прикладених до паралелепіпеда на його нижній і верхній гранях, обумовлені, наприклад, тим, що більш повільні вище розташовані шари рідини загальмовують шар, у якому перебуває паралелепіпед, а більш швидкі нижче розташовані шари «розганяють» його.

Тоді проекція рівнодіючих сил тертя на вісь х

.

Підставивши в це вираження значення дотичного напруження τ згідно рівняння (2.10) [, де µ - в'язкість рідини], одержимо

.

У більш загальному випадку тривимірного потоку складова швидкості w_x буде змінюватися не тільки в напрямку z, але й у напрямках всіх трьох осей координат. Тоді проекція рівнодіючих сил тертя на вісь х прийме вид

.

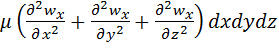Суму других похідних по осях координат називають оператором Лапласа:

.

Отже, проекція рівнодіючих сил тертя на вісь х може бути представлена як

Відповідно проекції рівнодіючих сил тертя на вісь y - , на вісь z - .

Проекції на осі координат рівнодіючої всіх сил (ваги, тиску і тертя), що діють на елементарний об’єм краплинної рідини (з урахуванням проекцій сил ваги й тиску, отриманих при виводі рівнянь Ейлера), становлять:

на вісь х

,

на вісь y

,

на вісь z

.

Суми проекцій сил на осі координат, відповідно до основного принципу динаміки, повинні дорівнювати добутку маси рідини ρdxdydz (ρ - густина рідини), що знаходиться в елементарному об’ємі, на проекції прискорення на осі координат. Тому, дорівнюючи проекції рівнодійної добуткам маси на проекції прискорення, після скорочення на dxdydz, одержимо

,

,                                        (2.35)

.

де відповідні субстанціональні похідні виражені для сталого й несталого потоків рівняннями (2.29) або (2.30).

Рівняння (2.35) являють собою рівняння Нав’є - Стокса, що описують рух в’язкої краплинної рідини.

Повний опис руху в’язкої рідини в його найбільш узагальненій формі включає в себе систему рівнянь Нав’є – Стокса, а також рівняння нерозривності потоку, які доповнюються відповідними умовами однозначності.

Однак, розв’язання такої системи рівнянь зустрічає непереборні труднощі і її безпосереднє використання для рішення практичних задач є неможливим. Тому в технічній гідравліці базуються в основному на рівняннях руху ідеальної рідини, застосовуючи поправні коефіцієнти та додаткові члени, що враховують фізичні особливості реальних рідин, або розв’язують задачу шляхом перетворень системи диференціальних рівнянь за допомогою теорії подібності.

     2.3.6. Подібність гідродинамічних процесів.

     Для визначення основних критеріїв подібності гідродинаміки запишемо рівняння переносу кількості руху Нав’є-Стокса (2.35) для моделі та натурного об’єкту в найбільш повному вигляді (для вертикальної осі z):

якщо для моделі рівняння має вигляд

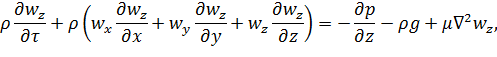
то для натури після множення всіх елементів цього рівняння на відповідні константи подібності:

,

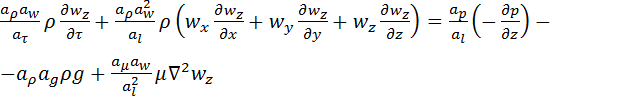де а_і – відповідні константи подібності (див. розділ 1.4.1).

      Для збереження тотожності отриманого й вихідного рівнянь дорівняємо всі комплекси коефіцієнтів, що стоять при однаковиx членах:

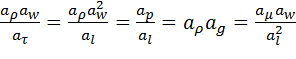                       (2.36)

                                     (1)        (2)        (3)       (4)         (5) 

Прирівнявши у вираженні (2.36) послідовно комплекси констант подібності (1), (3), (4), (5) з комплексом (2), одержимо співвідношення між відповідними силами й силами інерції:

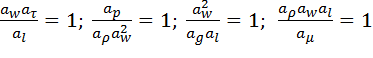             (2.37)

                                   (I)               (II)              (III)                (IV)

       Розглянемо співвідношення (IV) у вираженні (2.37). Заміняючи константи подібності на відношення відповідних величин, одержимо:

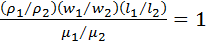, або ,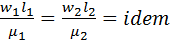

звідки                                           ,                              (2.38)

де Re - безрозмірне число, критерій Рейнольдса. Він характеризує відношення сил інерції до сил тертя й визначає режим руху у всіх подібних точках подібних систем.

Співвідношення (I) у рівнянні (2.37)  характеризує несталість руху рідини:

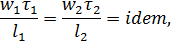
звідки

                                             (2.39)

Вираження (2.39) є критерієм подібності, що характеризує несталий стан процесу, і називається критерієм гомохронності. У всіх подібних точках подібних систем (натури й моделі) критерій гомохронності має однакове значення, якщо в цих системах рух несталий.

Зі співвідношення (II) одержимо критерій подібності, що характеризує відношення сил гідростатичного тиску до сил інерції в подібних системах:

.

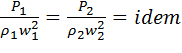Безрозмірне відношення   називають критерієм Ейлера. Між тім, при рішенні багатьох технічних задач гідродинаміки важливо визначати не абсолютний тиск Р у системі, а різницю тисків ΔР між якими-небудь точками або перерізами потоку рідини. Тому звичайно критерій Ейлера визначає вплив перепаду гідростатичного тиску на рух рідини й виражається в такий спосіб:

                                                                                        (2.40)

Нарешті, співвідношення (III) характеризує відношення сили ваги до сили інерції:

    .

Звідси одержуємо новий безрозмірний комплекс, який називають критерієм

Фруда, що визначає вплив сил ваги на рух рідини:

.                                           (2.41)

Таким чином, рішення рівняння Нав’є-Стокса, що описує в загальному виді процес руху в’язкої рідини, може бути представлене критеріальним рівнянням виду

=0                                       (2.42)

яке називають узагальненим критеріальним рівнянням гідродинаміки. Будь-яка задача руху  в’язкої рідини може бути вирішена шляхом знаходження залежності між критеріями, що входять у рівняння (2.42).

У рівнянні (2.42) всі критерії подібності, крім Eu, є визначальними, тому що вони складені тільки з величин, що виражають умови однозначності. Оскільки при рішенні практичних задач за допомогою рівняння (2.42) звичайно визначають величину ΔР, що входить в Eu, то в цьому випадку рівняння (2.42) записують щодо визначуваного критерію Eu:

                                                 (2.43)

Наприклад,

         ,                                      (2.44)

де значення А, q, n, т звичайно визначають дослідним шляхом.

У ряді випадків рівняння (2.43) доповнюють геометричним симплексом, що характеризує вплив співвідношення довжини каналу і його діаметра – l/d_е.

При усталеному русі критерій гомохронності може бути виключений з рівняння (2.42); тоді                                                            (2.45)

У тому випадку, якщо швидкість руху рідини важко визначається (наприклад, при природній конвекції), уводять так звані похідні, або модифіковані критерії подібності, складені з основних критеріїв. У цих похідних критеріях величина, яка  важко визначається при проведенні дослідів, замінюється іншими величинами, які порівняно просто визначаються аналітично або експериментально.

Наприклад, при природній конвекції, що виникає внаслідок різниці густини рідини, обумовленої різницею температур у різних точках цієї рідини, важко визначити швидкість руху конвекційних токів. Критерій Фруда визначає дію сил ваги, внаслідок яких відбувається переміщення часток рідини, але в нього входить важко визначувана величина w. Для того щоб виключити величину w із критерію , беруть відношення двох критеріїв:

Отриманий безрозмірний комплекс величин є похідним критерієм і називається критерієм Галілея:

                                                                        (2.46)

   Якщо помножити цей критерій на відношення  (де ρ₀ і ρ –густина рідини в різних точках), що визначає причину виникнення конвекційних токів, одержимо новий похідний критерій подібності - критерій Архімеда:

(2.47)

У подібних системах, у яких процеси протікають в умовах природної конвекції під дією сили ваги, необхідне дотримання рівності критеріїв Ga або Аr.

У багатьох випадках використовують досить формальний, але більш простий спосіб подібного перетворення диференціальних рівнянь, що полягає в наступному: критерії подібності знаходять шляхом ділення одного члена рівняння на інший й наступного відкидання знаків математичних операторів. Наприклад, для рівняння Нав’є-Стокса (2.35) таке перетворення зведеться до наступного:

;  ;    ;    .

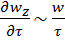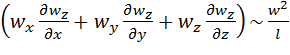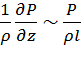Прийнявши за масштаб силу інерції й поділивши на неї всі інші, одержимо вже відомі критерії подібності гідродинамічних процесів: Но, Еu, Fr, Rе. Аналогічним чином можна одержати критерії подібності для процесів тепло- і масообміну, що й буде показано у відповідних розділах.