Основное уравнение молекулярно-кинетической теории газов. Абсолютный нуль температуры.

Основное уравнение молекулярно-кинетической теории газов.

Абсолютный нуль температуры

Вспомним основные сведения про модель идеального газа:

·                     молекулы движутся хаотически;

·                     механизм давления идеального газа – это соударение отдельных молекул со стенками сосуда.

Пусть идеальный газ находится в цилиндрическом сосуде (см. рис. 1). Определим давление p этого газа на поршень.

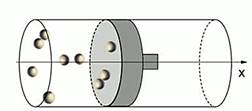
Рис. 1. Идеальный газ (молекулы) в цилиндрическом сосуде

По определению давление – величина, равная отношению силы (F), действующей перпендикулярно поверхности, к площади этой поверхности (S).

Вычислим силу (F), с которой молекулы действуют на поршень:

1. Определим силу удара одной молекулы о стенку сосуда.

Пусть молекула идеального газа массой  движется в плоскости XOYсо скоростью  и, ударившись о поршень, отскакивает от него со скоростью  (см. рис. 2). Согласно второму закону Ньютона, сила, действующая на молекулу со стороны поршня во время удара, равна:

,

где a – ускорение молекулы при ударе;   – изменение скорости движения молекулы при ударе;  – продолжительность удара.

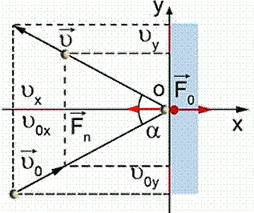
Рис. 2. Столкновение молекулы с поршнем

Проекция скорости на ось OY не изменяется, поэтому всё изменение скорости  равно изменению скорости вдоль оси X:

Так как:

То:

Согласно третьему закону Ньютона, сила, с которой молекула действует на поршень, равна по модулю силе , с которой поршень действует на молекулу. Следовательно:

2. Рассчитаем число молекул N, ударившихся о поршень за интервал .

За интервал времени  до поршня успеют долететь только те молекулы, которые движутся в направлении поршня и удалены от него на расстояние  (см. рис. 3). То есть фактически половина числа молекул, заключённых в цилиндре объёмом . Следовательно, число молекул, ударившихся о поршень за интервал , равно:

 – общее число молекул, которое равно произведению концентрации на объём:

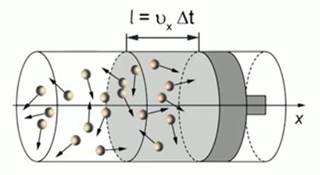
Рис. 3. Молекулы, ударившиеся о поршень за время 

3. Определим общую силу ударов молекул о поршень.

Эта сила будет равна произведению силы удара одной молекулы на общее число ударов:

Мы живём в трёхмерном мире, то есть любая молекула имеет проекцию скорости . Так как все молекулы двигаются хаотично, то направления их движения равноправные, поэтому можно написать, что в среднем, для средней квадратичной скорости,  одинаковые (). Следовательно, заменяем квадрат проекции скорости на средний квадрат проекции скорости:

Подставляем это значение в формулу силы ударов молекул о поршень:

Значение данной силы подставим в формулу давления:

 – основное уравнение МКТ идеального газа,

где макропараметры ;

микропараметры .

Второй способ записи основного уравнения МКТ

Основное уравнение МКТ можно записать в другом виде, в котором давление связывается не с массой и скоростью молекулы, а с их комбинацией, то есть со средней кинетической энергией одной молекулы.

Среднюю кинетическую энергию поступательного движения молекул газа можно рассчитать по формуле:

Следовательно, основное уравнение МКТ будет выглядеть так:

 – давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Температура – это мера того, сколько тепловой энергии в системе.

Это измерение означает, что все атомы и молекулы, которые движутся вокруг, имеют определенное количество кинетической энергии (и менее очевидно потенциальной энергии). Когда все молекулы (или атомы) в системе полностью перестают двигаться, это так холодно, что ниже уже нельзя получить. Это состояние, где вообще нет тепловой энергии, называется абсолютный ноль температуры.

Численно абсолютный ноль температуры записывается как ⁰K или -273.15°C

Понятие абсолютного нуля

Абсолютный ноль температуры по сути понимание того, сколько энергии доступно от молекул газа в законе идеального газа.

Степень нагревания должна быть измерена в абсолютном масштабе (как Кельвин), чтобы закон идеального газа имел смысл. Идеальный газ – отсутствуют силы межмолекулярного воздействия. Кроме того, идея абсолютного нуля играет важную роль в физике излучения абсолютно черного тела (сколько энергии излучает объект при определенной температуре) и максимально возможный КПД теплового двигателя (так называемый КПД Карно).

Понятие абсолютный ноль температуры также является частью физики изменения климата.

Средняя температура Земли, которая составляет около 15°C, будет 288 K. Если парниковые газы увеличат температуру планеты на 1%, то она не поднимется на 0,15 градуса, она поднимется на 2,88 градуса.

Кельвин и Цельсий имеют одинаковое приращение степени, но Кельвин-абсолютная шкала (что означает, что нулевая точка действительно равна нулю), а Цельсий – относительная шкала (нулевая точка произвольна – она была выбрана ученым). Вот почему температура будет увеличиваться на 2,88 градуса вместо 0,15 градуса. Понимание того, как эти небольшие процентные изменения температуры Земли могут привести к радикальным последствиям для планеты, является важной частью климатологии.

Термодинамика показала, что добраться до абсолютного нуля температуры невозможно, но физики подобрались достаточно близко. Используя лазерное охлаждение и магнитную ловушку, экспериментально ученые смогли охладить атомы до температуры нескольких нK (10^-9 K), чтобы сформировать конденсаты Бозе-Эйнштейна.

В неидеальных условиях самая низкая возможная температура из-за воздействия звезд 2,725 градусов Кельвина,  -270,425 градусов Цельсия.

Температура – это показания термометра, который измеряет, насколько горячее или холодное вещество. На микроскопическом уровне она характеризует среднюю кинетическую энергию молекул внутри материала или системы. Это измеримое физическое свойство объекта и может рассматриваться с другими измеримыми физическими свойствами, такими как скорость, масса и плотность и т.п.

АБСОЛЮТНАЯ ШКАЛА ТЕМПЕРАТУР

- введена английским физиком У. Кельвином

- нет отрицательных температур

Единица абсолютной температуры в СИ: [T] = 1K (Кельвин)

Нулевая температура абсолютной шкалы - это абсолютный ноль ( 0К = -273oС ), самая низкая температура в природе.

В настоящее время достигнута самая низкая температура - 0,0001К.

По величине 1К равен 1^oC.

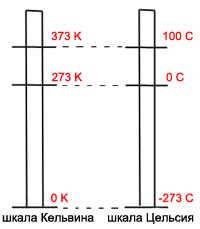
Связь абсолютной шкалы со шкалой Цельсия

Запомни!

В формулах абсолютная температура обозначается буквой «Т»,

а температура по шкале Цельсия буквой «t».

Скачано с www.znanio.ru