
Лекция 3
ОСНОВЫ ЛОГИКИ
Логические основы компьютеров . Алгебра логики
ОСНОВЫ ЛОГИКИ
Логические основы компьютеров . Алгебра логики
1. Определения
2. Логические связки Тренировочные задания.
3. Таблицы истинности
4. Логическая формула
4.1. Примеры
5. Логические законы
5.1. Упрощение логических выражений
6. Как решать логические задачи?
I. Решение логических задач средствами алгебры логики II. Решение логических задач табличным способом
III. Решение логических задач с помощью рассуждений 7. Какая связь между алгеброй логики и двоичным кодированием?
7.1. Логические основы устройства КП
8. Что такое переключательная схема? (Дополнительно) Карточки для студентов. Решение логических задач
Логика – наука о способах и формах мышления.
Возникла в Древнем Китае и Индии. Основоположником формальной логики считается Аристотель.
Логика позволяет, отвлекаясь от содержательной стороны, строить формальные модели окружающего мира. Свойства, связи и отношения объектов окружающего мира в сознании человека отражают законы логики.
Мышление всегда осуществляется в следующих формах:
![]() Понятие форма мышления, отражающая существенные
свойства, связи и отношения предметов и явлений в их противоречии и развитии
Понятие форма мышления, отражающая существенные
свойства, связи и отношения предметов и явлений в их противоречии и развитии
![]() Умозаключение – форма мышления, с помощью которой
из одного ил нескольких суждений может быть получено новое суждение.
Умозаключение – форма мышления, с помощью которой
из одного ил нескольких суждений может быть получено новое суждение.
![]() Логическое высказывание – форма мышления, в котором что-либо утверждается или
отрицается о свойствах реальных предметов и отношениях между ними. Высказывание
может быть либо истинным либо ложным
Логическое высказывание – форма мышления, в котором что-либо утверждается или
отрицается о свойствах реальных предметов и отношениях между ними. Высказывание
может быть либо истинным либо ложным
Проще говоря Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Так, например, предложение ―6 — четное число‖ следует считать высказыванием, так как оно истинное. Предложение ―Рим — столица Франции‖ тоже высказывание, так как оно ложное.
![]() Разумеется, не всякое предложение
является логическим высказыванием. Высказываниями не являются, например,
предложения ―студент 2 курса‖ и ―информатика —
сложный предмет‖. Первое предложение ничего не утверждает об ученике,
а второе использует слишком неопределѐнное понятие ―сложный
предмет‖. Вопросительные и восклицательные предложения также не
являются высказываниями, поскольку говорить об их истинности или ложности не
имеет смысла.
Разумеется, не всякое предложение
является логическим высказыванием. Высказываниями не являются, например,
предложения ―студент 2 курса‖ и ―информатика —
сложный предмет‖. Первое предложение ничего не утверждает об ученике,
а второе использует слишком неопределѐнное понятие ―сложный
предмет‖. Вопросительные и восклицательные предложения также не
являются высказываниями, поскольку говорить об их истинности или ложности не
имеет смысла.
Предложения типа ―в городе A более миллиона жителей‖, ―у него голубые глаза‖ не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание ―площадь поверхности Индийского океана равна 75 млн кв. км‖ в одной ситуации можно посчитать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик
Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.
Что же такое логическое высказывание?
В алгебре высказываний простым (элементарным) высказываниям ставятся в соответствие логические переменные. Истинному высказыванию соответствует значение логической переменной 1, а ложному – 0. Над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.
Для образования составных высказываний используют базовые логические операции:
1) Инверсия
2) Конъюнкция
3) Дизъюнкция
И функции
4) Импликация
5) Эквивалентность
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний. При этом каждому элементарному высказыванию присваивается имя, а принимаемые ими значения ―истина‖ или ―ложь‖, обозначают, соответственно, ―1‖ и ―0‖.
Правила определения истинности составных высказываний.
Пусть А и В – элементарные высказывания, тогда:
1.
![]() Инверсия (лог отрицание -
НЕ) Обозначение: ¬А или .
Инверсия (лог отрицание -
НЕ) Обозначение: ¬А или .
Высказывание истинно, когда A ложно, и ложно, когда A истинно.
2. Конъюнкция (лог. умножение, И) (лат. conjunctio — соединение).
Обозначение: А&В или А^В или А•В
Высказывание А•В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Например, высказывание
―Москва – столица России и самый большой город России‖ – истинно, а ―Москва – столица России и самый большой город мира‖ – ложно.
3. Дизъюнкция (лог. сложение, ИЛИ) (лат. disjunctio — разделение)
Обозначение: АvВ или А+В
Высказывание АvВ ложно тогда и только тогда, когда оба высказывания А и В ложны.
Например, высказывание
― Столица России Москва или Санкт–Петербург‖ – истинно, а
― Столица России Новокузнецк или Санкт–Петербург ‖ – ложно.
4. Импликация (лог. следование, «если то») (лат. implico — тесно связаны) Обозначение: - А→В
![]() Высказывание
А В ложно тогда и только тогда, когда А истинно, а В — ложно.
Высказывание
А В ложно тогда и только тогда, когда А истинно, а В — ложно.
![]() Импликацию
можно выразить через дизъюнкцию и отрицание: А В = v В.
Импликацию
можно выразить через дизъюнкцию и отрицание: А В = v В.
Каким же образом импликация связывает два элементарных высказывания?
![]()
![]() Покажем это на примере высказываний: ―данный
четырѐхугольник — квадрат‖ (А) и ―около данного
четырѐхугольника можно описать окружность‖ (В). Рассмотрим
составное высказывание А В, понимаемое как ―если данный
четырѐхугольник квадрат, то около него можно описать окружность‖.
Есть три варианта, когда высказывание А В истинно:
Покажем это на примере высказываний: ―данный
четырѐхугольник — квадрат‖ (А) и ―около данного
четырѐхугольника можно описать окружность‖ (В). Рассмотрим
составное высказывание А В, понимаемое как ―если данный
четырѐхугольник квадрат, то около него можно описать окружность‖.
Есть три варианта, когда высказывание А В истинно:
А истинно и В истинно, то есть данный четырѐхугольник квадрат, и около него можно описать окружность;
А ложно и В истинно, то есть данный четырѐхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырѐхугольника);
A ложно и B ложно, то есть данный четырѐхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант: А истинно и В ложно, то есть данный четырѐхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка ―если ..., то‖ описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться ―бессмысленностью‖ импликаций, образованных высказываниями, совершенно не связанными по содержанию.
Например, такими:
―если президент США — демократ, то в Африке водятся жирафы‖, ―если арбуз — ягода, то в бензоколонке есть бензин‖.
5. Эквивалентность (лог. равенство, ―тогда и только тогда‖, "необходимо и достаточно‖, ―... равносильно ...‖)
Обозначение: А~В или А![]()
Высказывание А ~ В истинно тогда и только тогда, когда значения А и В совпадают.
Эквиваленцию
можно выразить через отрицание, дизъюнкцию и конъюнкцию: А ![]() В = (
В = (![]() v В) • (
v В) • (![]() v А).
v А).
Например, высказывание
―24 делится на 6 тогда и только тогда, когда 24 делится на 3 истинно, а высказывание ―24 делится на 6 тогда и только тогда, когда 24 делится на 5‖ ложно. Высказывания А и В, образующие составное высказывание А ~ В, могут быть совершенно не связаны по содержанию, например: ―три больше двух‖ (А), ―пингвины живут в Антарктиде‖ (В). Образованное из высказываний А, В составные высказывания A~ B истинно.
6. Приоритет: инверсия (отрицание), Конъюнкция (лог. умножение И), Дизъюнкция (лог. сложение ИЛИ), Импликация (лог. следование), Эквивалентность (лог. равенство). Изменить порядок выполнения логических операций можно с помощью круглых скобок.
Тренировочные задания.
1.
![]() Для
какого Х истинно высказывание: X 1 ((X 5) (X
3))
Для
какого Х истинно высказывание: X 1 ((X 5) (X
3))
1) 1
2) 2
3) 3
4) 4
2.
![]() Для
какого Х истинно высказывание: (X
4) ((X 1) (X 4))
Для
какого Х истинно высказывание: (X
4) ((X 1) (X 4))
1) 1
2) 2
3) 3
4) 4
Для каждого составного высказывания (лог. выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.
|
А |
В |
А^В - И |
А V В – ИЛИ |
Не А |
А→В если-то |
А~В |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Как составить таблицу истинности?
1. Количество строк N=2n, где n – количество переменных, входящих в высказывание.
2. Количество столбцов – количество переменных + количество операций.
Примеры.
1.
![]() (A B) (A B)
(A B) (A B)
|
А |
В |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
2.
Составим таблицу истинности для формулы (ОШИБКА – пропущено
отрицание над первым х) ![]() , которая содержит две переменные x
и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих
переменных, в последующих столбцах — значения промежуточных формул и в
последнем столбце — значение формулы. В результате получим таблицу:
, которая содержит две переменные x
и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих
переменных, в последующих столбцах — значения промежуточных формул и в
последнем столбце — значение формулы. В результате получим таблицу:
|
Перем |
енные |
Промежуточные ло |
гические формулы |
Формула |
|||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула
![]() принимает значение 1, то есть
является тождественно истинной.
принимает значение 1, то есть
является тождественно истинной.
3
(дома). Таблица истинности для формулы ![]() :
:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Из
таблицы видно, что при всех наборах значений переменных x и y формула ![]() принимает
значение 0, то есть является тождественно ложной.
принимает
значение 0, то есть является тождественно ложной.
3.
(дома) Таблица истинности для формулы ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
Из
таблицы видно, что формула ![]() в некоторых случаях принимает значение
1, а в некоторых — 0, то есть является выполнимой.
в некоторых случаях принимает значение
1, а в некоторых — 0, то есть является выполнимой.
Составное высказывание можно рассматривать как некую логическую функцию.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. Определение логической формулы:
1. Всякая логическая переменная и символы ―истина‖ (―1‖) и ―ложь‖ (―0‖) — формулы.
2.
![]() Если А и В — формулы, то
Если А и В — формулы, то ![]() , (А • В), (А v В), (А B), (А В)
— формулы.
, (А • В), (А v В), (А B), (А В)
— формулы.
3. Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
![]() В качестве примера рассмотрим высказывание ―если я
куплю яблоки или абрикосы, то приготовлю фруктовый пирог‖. Это
высказывание формализуется в виде (AvB) C; такая же формула
соответствует высказыванию ―если Игорь знает английский или японский
язык, то он получит место переводчика‖.
В качестве примера рассмотрим высказывание ―если я
куплю яблоки или абрикосы, то приготовлю фруктовый пирог‖. Это
высказывание формализуется в виде (AvB) C; такая же формула
соответствует высказыванию ―если Игорь знает английский или японский
язык, то он получит место переводчика‖.
![]() Как показывает анализ формулы (A v B) C, при
определѐнных сочетаниях значений переменных A, B и C она принимает значение
―истина‖, а при некоторых других сочетаниях — значение
―ложь‖ (разберите самостоятельно эти случаи). Такие формулы
называются выполнимыми.
Как показывает анализ формулы (A v B) C, при
определѐнных сочетаниях значений переменных A, B и C она принимает значение
―истина‖, а при некоторых других сочетаниях — значение
―ложь‖ (разберите самостоятельно эти случаи). Такие формулы
называются выполнимыми.
Формулы называются тождественно истинными или тавтологиями, если при любых значениях входящих в них логических переменных они принимают истинное значение.
Высказывания, которые формализуются тавтологиями называются логически истинными высказываниями.
Например, формула А v![]() (или),
соответствующая высказыванию ―Этот треугольник прямоугольный или
косоугольный‖. Эта формула истинна и тогда, когда треугольник
прямоугольный, и тогда, когда треугольник не прямоугольный.
(или),
соответствующая высказыванию ―Этот треугольник прямоугольный или
косоугольный‖. Эта формула истинна и тогда, когда треугольник
прямоугольный, и тогда, когда треугольник не прямоугольный.
Формулы называются тождественно ложными формулами или противоречиями, если при любых значениях входящих в них логических переменных они принимают ложное значение.
Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Например, формула А •![]() (и), которой соответствует, например, высказывание ―Яблоко
– это фрукт и Яблоко – это овощ‖. Очевидно, что эта формула ложна,
так как либо А, либо
(и), которой соответствует, например, высказывание ―Яблоко
– это фрукт и Яблоко – это овощ‖. Очевидно, что эта формула ложна,
так как либо А, либо ![]() обязательно ложно.
обязательно ложно.
Если две формулы А и В ―одновременно‖, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
![]() Равносильность
двух формул алгебры логики обозначается символом ―=‖ или символом
― ‖.
Равносильность
двух формул алгебры логики обозначается символом ―=‖ или символом
― ‖.
1. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y Z. Дан фрагмент таблицы истинности:
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
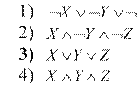
2. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y Z. Дан фрагмент таблицы истинности:
|
X |
Y |
Z |
F |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1) X Y Z
2) X Y Z
3)
 X Y Z
X Y Z
4) X Y Z
3. Сколько различных решений имеет уравнение
![]() (K L M) ( L M
N) 1, где К,L,M,N – логические переменные?
(K L M) ( L M
N) 1, где К,L,M,N – логические переменные?
1) 1
2) 2
3) 3
4) 4
Решение.
Одно из слагаемых должно быть =1:
![]() (K L M) 1, когда
К=L=M=1, а N- любое. Следовательно – 2 решения. ( L M N) 1, когда L=M=0, N=1, К – любое,
Следовательно – еще 2 решения.
(K L M) 1, когда
К=L=M=1, а N- любое. Следовательно – 2 решения. ( L M N) 1, когда L=M=0, N=1, К – любое,
Следовательно – еще 2 решения.
Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:
1) Закон тождества – всякое высказывание равносильно самому себе. А=А
2) Закон непротиворечия – высказывание не может быть одновременно истинным и ложным:
![]() А и не А = 0
А и не А = 0
3) Закон исключенного третьего – высказывание либо ложно либо истинно.
![]() А
или не А =1
А
или не А =1
4) Закон двойного отрицания:
![]() не
не А = А
не
не А = А
5)
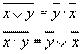 Законы де Моргана не (А или В) = не А и не В
Законы де Моргана не (А или В) = не А и не В
не (А и В) = не А или не В
6) Закон коммутативности (Переместительный) – от перемены мест результат не меняется
![]() А и
В= В и А
А и
В= В и А
А или В= В или А
7) Закон ассоциативности (Сочетательный) если в лог.выражении используются только И или ИЛИ, то скобки можно не ставить или ставить как угодно
![]() (А
и В) и С= А и (В и С)
(А
и В) и С= А и (В и С)
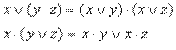 (А или В) или С= А или (В или С) 8) Закон дистирубтивности
(Распределительный) – вынос за скобки как общие множители так и общие слагаемые
м-ка: ab+ac=a(b+c) (А и В) или (А и С) = А и (В или С)
(А или В) или С= А или (В или С) 8) Закон дистирубтивности
(Распределительный) – вынос за скобки как общие множители так и общие слагаемые
м-ка: ab+ac=a(b+c) (А и В) или (А и С) = А и (В или С)
(А или В) и (А или С) = А или (В и С)
9) Закон Идемпотенции
![]()
10) Закон Поглощения
![]()
11) Закон Склеивания
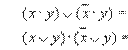
12) Операция с константами:
![]()
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определѐнному виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
Разобрать примеры и с записью логических операций словами и с записью символами!
1) Упростить лог. выражение (А и В) или (А и не В).
= (дистрибутивность) А и (В или не В) =
= (з-н исключенного третьего В или НЕ В=1) А и 1 = А
2) Какая из заданных логических функций является эквивалентной А? А и не А или не А
А и не А или В
А и не В и А А и не В или А Ответ:
А и не А или не А = 0 или не А= не А
А и не А или В= 0 или В=В
А и не В и А = А и не В
А и не В или А = А
3)
![]() Какое
логическое выражение равносильно выражению: (A B) С ?
Какое
логическое выражение равносильно выражению: (A B) С ?
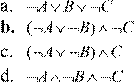
4) ![]() Какое логическое выражение
равносильно выражению: ( A B)
Какое логическое выражение
равносильно выражению: ( A B)
a. A B
b. A B
c.
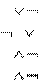 В A
В A
d. А В
5) Упростить:
1)
![]()
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с еѐ инверсией и правило операций с константами);
2)
![]()
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с еѐ инверсией);
3)
![]()
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
4)
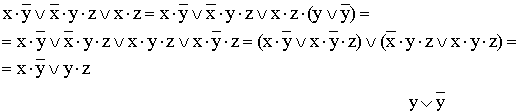 (вводится вспомогательный логический сомножитель ( );
затем комбинируются два крайних и два средних логических слагаемых и
используется закон поглощения);
(вводится вспомогательный логический сомножитель ( );
затем комбинируются два крайних и два средних логических слагаемых и
используется закон поглощения);
5)
![]()
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6)
![]()
(выносятся за скобки общие множители; применяется правило операций с константа-
ми);
7)
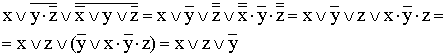
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8)
![]()
(общий множитель x выносится за скобки, комбинируются
слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции ![]() применяется
правило операции переменной с еѐ инверсией);
применяется
правило операции переменной с еѐ инверсией);
9)
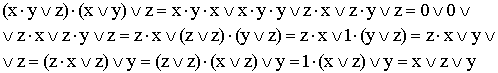
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10)
![]()
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Из этих примеров
видно, что при упрощении логических формул не всегда очевидно, какой из законов
алгебры логики следует применить на том или ином шаге. Навыки приходят с
опытом.
6. Как решать логические задачи?
![]() Разнообразие
логических задач очень велико. Способов их решения тоже немало. Но наибольшее
распространение получили следующие три способа решения логических задач: средствами
алгебры логики; табличный; с помощью
рассуждений.
Разнообразие
логических задач очень велико. Способов их решения тоже немало. Но наибольшее
распространение получили следующие три способа решения логических задач: средствами
алгебры логики; табличный; с помощью
рассуждений.
I. Решение логических задач средствами алгебры логики Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
4. определяются значения истинности этой логической формулы;
5. из полученных значений истинности формулы определяются значения истинности введѐнных логических высказываний, на основании которых делается заключение о решении.
Пример 1. Трое друзей спорили о результатах чемпионата по футболу.
— Вот увидишь, «Динамо» не будет первым, — сказал Иван. - Первым будет «Зенит». — Победителем будет «Динамо», — воскликнул Николай. — «Спартаку» не быть первым.
Петр, к которому обратился Николай, возмутился:
— «Зениту» не видать первого места, а вот у «Спартака» новый тренер.
По завершении чемпионата оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто победил?
Решение. Введем обозначения для логических высказываний:
Д — победит «Динамо»; З — победит «Зенит»Хилл; С — победит «Спартак». Реплика Николая "У «Спартака» новый тренер" не содержит никакого утверждения о месте, которое займѐт команда, поэтому в дальнейших рассуждениях не учитывается. Зафиксируем высказывания каждого из друзей:
![]()
![]()
![]() Иван :Д З, Николай :Д С, Петр :З
Иван :Д З, Николай :Д С, Петр :З
Учитывая то, что предположения двух друзей ((каких неизвестно, поэтому три выражения через или)), а предположения третьего неверны, запишем и упростим истинное высказывание
(Д З) (Д С) З (Д З) (Д С) З (Д З) (Д С) З
(1Д4З4)42(Д4С4)43З (1Д4З4)4(2Д44С)43З (Д З) (Д С) З
сокращаем:Диотрицание 0 сокращаемЗиотрицание 0
значитлог.умножение 0 значитлог.умножение 0
 0 0 (Д З) Д С З (Д Д
С З) (З Д С З) (Д С З) (З Д С) (З Д С)
0 0 (Д З) Д С З (Д Д
С З) (З Д С З) (Д С З) (З Д С) (З Д С)
Высказывание (З Д С) 1 истинно только при Д=1, З=0, С=0.
Ответ. Победитель – «Динамо».
Пример 2. Кто из четырех мальчиков разбил вазу, если Саша, Ваня, Коля и Олег делают вид, что происшедшее к ним не относится.
— Коля не бил по мячу, — сказал Саша. — Это сделал Ваня.
Ваня ответил: «Разбил Коля, Саша не играл в футбол дома».
Коля сказал: «Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки». Олег сказал: «А меня не было в комнате. Я был в библиотеке».
Оказалось, что один из мальчиков оба раза солгал, а трое в каждом из своих заявлений говорили правду.

II. Решение логических задач табличным способом
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Пример 3. В симфонический оркестр приняли на работу трѐх музыкантов: Бориса, Сергея и Владимира, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Сергей самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Борис любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Сергей мирит их;
5. Борис не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Из условия 4 следует, что Сергей не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое.
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
|
|
0 |
0 |
|
Сергей |
|
|
0 |
|
|
0 |
|
Владимир |
|
|
|
|
|
|
Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Следовательно, инструменты Бориса — альт и кларнет.
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
1 |
1 |
0 |
0 |
|
Сергей |
|
|
0 |
|
|
0 |
|
Владимир |
|
|
|
|
|
|
Тогда оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями:
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
1 |
1 |
0 |
0 |
|
Сергей |
|
|
0 |
0 |
|
0 |
|
Владимир |
|
|
0 |
0 |
|
|
Из таблицы видно, что на трубе может играть только Владимир.
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
1 |
1 |
0 |
0 |
|
Сергей |
|
|
0 |
0 |
|
0 |
|
Владимир |
|
|
0 |
0 |
|
1 |
Из условий 1 и 2 следует, что Сергей не скрипач.
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
1 |
1 |
0 |
0 |
|
Сергей |
0 |
|
0 |
0 |
|
0 |
|
Владимир |
|
|
0 |
0 |
|
1 |
Тогда получается, что во-первых, Сергей играет на флейте и гобое, а во-вторых, скрипачом является Владимир.
|
|
скрипка |
флейта |
альт |
кларнет |
гобой |
труба |
|
Борис |
0 |
0 |
1 |
1 |
0 |
0 |
|
Сергей |
0 |
1 |
0 |
0 |
1 |
0 |
|
Владимир |
1 |
|
0 |
0 |
|
1 |
Оба инструмента, на которых играет Владимир, теперь определены, поэтому остальные клетки строки "Владимир" можно заполнить нулями.
Ответ: Борис играет на альте и кларнете, Сергей — на флейте и гобое, Владимир — на скрипке и трубе.
Пример 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
|
Имя |
Юра |
|
|
|
Профессия |
|
врач |
|
|
Увлечение |
|
туризм |
|
Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:
|
Имя |
Юра |
Тимур |
Влад |
|
Профессия |
физик |
врач |
юрист |
|
Увлечение |
бег |
туризм |
регби |
Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
III. Решение логических задач с помощью рассуждений Этим способом обычно решают несложные логические задачи.
Пример 5. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
1. Вадим изучает китайский; 2. Сергей не изучает китайский;
3. Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи (что только одно утверждение истинно), поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Домашняя работа.
Пример 6. Четыре школьника, Миша (М), Коля (К), Сергей (С) и Петр (П), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:
Миша: «Я не бил окно, и Коля тоже...»
Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!» Сергей: «Я не делал этого, стекло разбил Миша».
Петр: «Я не делал этого, я выходил в этот момент в коридор».
Стало известно, что двое из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.
Кто разбил стекло в классе?
Пример 7. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
7. Какая связь между алгеброй логики и двоичным кодированием?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: ―1‖ и ―0‖.
Из этого следует два вывода:
1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
В основу обработки компьютером информации лежит алгебра логики.
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.
Базовые логические элементы реализуют три основные операции:
§ Логический элемент НЕ – инверсию
§ Логический элемент И – лог. умножение
§ Логический элемент ИЛИ – лог. сложение
|
Базовая схема |
Графическое обозначение |
Таблица истинности |
||||||||
|
Схема НЕ (инвертор) преобразует сигнал в противоположный, например, если на вход элемента подана логическая 1, то на выходе этого элемента будет логический 0 и наоборот. |
|
|
x |
x |
|
|||||
|
0 |
1 |
|||||||||
|
1 |
0 |
|||||||||
|
|
||||||||||
|
Схема И (конъюнктор) преобразует два сигнала, поданных на вход, в один сигнал на выходе по правилу логической операции И. |
|
|
x |
y |
x·y |
|
||||
|
0 |
0 |
0 |
||||||||
|
0
1 |
1
1 |
0
1 |
||||||||
|
Схема ИЛИ (дизъюнктор) преобразует два сигнала, поданных на вход, в один сигнал на выходе по правилу: когда хотя бы на одном входе схемы ИЛИ будет единица, на еѐ выходе также будет единица. |
Х У ХvУ
|
|
|
|
x v y |
|
||||
|
|
|
0 |
||||||||
|
|
|
1 |
||||||||
|
|
|
1 |
||||||||
![]()
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства ПК, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов. Из миллионов таких элементов строится ЭВМ. Данные принципы применяются в след. устройствах ПК:
1) Триггер – электронная схема, которая является структурной единицей оперативной памяти ПК и внутренних регистров процессора, может хранить1 бит информации. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.
Термин триггер происходит от английского слова trigger — защѐлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает ―хлопанье‖. Это звукоподражательное название электронной схемы указывает на еѐ способность почти мгновенно переходить (―перебрасываться‖) из одного электрического состояния в другое и наоборот. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 • 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
2) Сумматор – электронная логическая схема, обеспечивающая сложение двоичных чисел.
В целях максимального упрощения работы ПК все многообразие математических операций в процессоре сводится к сложению двоичных чисел.
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
Рассмотрим, как из логических элементов можно сконструировать устройство для сложения двух двоичных чисел – одноразрядный сумматор или полусумматор. Это устройство должно давать на выходе следующие сигналы:
0+0=00
0+1=01
1+0=01
1+1=10
Составим таблицу истинности:, обозначив слагаемые X и Y, а результаты: P и Z
|
X |
Y |
|
P |
Z |
|
0 |
0 |
|
0 |
0 |
|
0 |
1 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
1 |
1 |
|
1 |
0 |
Логическая функция X и Y (X или Y) и не (X и Y)
В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоѐмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаѐтся и с которых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен 0.
Будем
считать, что два переключателя Х и ![]() связаны таким образом,
что когда Х замкнут, то
связаны таким образом,
что когда Х замкнут, то ![]() разомкнут, и наоборот. Следовательно, если
переключателю Х поставлена в соответствие логическая переменная х, то
переключателю
разомкнут, и наоборот. Следовательно, если
переключателю Х поставлена в соответствие логическая переменная х, то
переключателю ![]() должна соответствовать переменная
должна соответствовать переменная ![]() .
.
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную 1, если схема проводит ток, и равную 0 — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
Найдем функции проводимости F некоторых переключательных схем:
a)
![]()
Схема не содержит переключателей и проводит ток всегда, следовательно F=1;
б)
![]()
Схема содержит один постоянно разомкнутый контакт, следовательно F=0;
в)
![]()
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x;
г)
![]()
Схема проводит ток, когда переключатель х разомкнут, и не
проводит, когда х замкнут, следовательно, F(x) = ![]() ;
;
д)
![]()
![]() Схема
проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = xy;
Схема
проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = xy;
е)
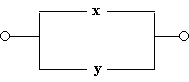
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x)=x v y;
ж)
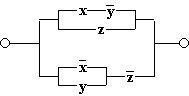
Схема состоит из двух параллельных ветвей и описывается функцией
![]() .
.
Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале).
Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.
Задача нахождения среди равносильных схем наиболее простых является очень важной. Большой вклад в ее решение внесли российские учѐные Ю.И. Журавлев, С.В. Яблонский и др.
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трѐм этапам:
1. составлению функции проводимости по таблице истинности, отражающей эти условия;
2. упрощению этой функции;
3. построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к
1. определению значений еѐ функции проводимости при всех возможных наборах входящих в эту функцию переменных.
2. получению упрощѐнной формулы.
Примеры.
1. Построим схему, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трѐх контактов.
Решение. В этом случае можно обойтись без построения
таблицы истинности. Очевидно, что функция проводимости имеет вид F(x, y, z,
t) = t ![]() (x v y v z), а схема выглядит так:
(x v y v z), а схема выглядит так:
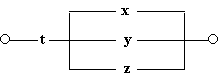
2. Найдем функцию проводимости схемы:
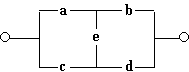
Решение. Имеется четыре возможных пути прохождения тока при замкнутых переключателях a, b, c, d, e : через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b.
![]() Функция проводимости F(a,
b, c, d, e) = a b v a e d v c d v c e b.
Функция проводимости F(a,
b, c, d, e) = a b v a e d v c d v c e b.
3. Упростим переключательные схемы:
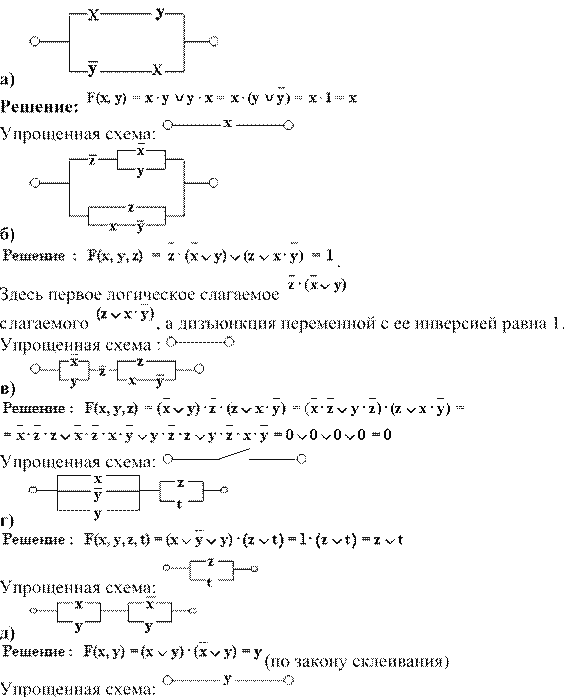 (ОШИБКА
в рис. Пропущено отрицание)
(ОШИБКА
в рис. Пропущено отрицание)
является отрицанием второго логического
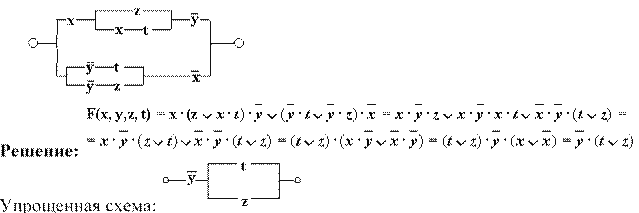 е)
е)
Карточки для студентов.
Решение логических задач Пример 1. Трое друзей спорили о результатах чемпионата по футболу.
— Вот увидишь, «Динамо» не будет первым, — сказал Иван. - Первым будет «Зенит». — Победителем будет «Динамо», — воскликнул Николай. — «Спартаку» не быть первым.
Петр, к которому обратился Николай, возмутился:
— «Зениту» не видать первого места, а вот у «Спартака» новый тренер.
По завершении чемпионата оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто победил?
Пример 2. Кто из четырех мальчиков разбил вазу, если Саша, Ваня, Коля и Олег делают вид, что происшедшее к ним не относится.
— Коля не бил по мячу, — сказал Саша. — Это сделал Ваня.
Ваня ответил: «Разбил Коля, Саша не играл в футбол дома».
Коля сказал: «Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки». Олег сказал: «А меня не было в комнате. Я был в библиотеке».
Оказалось, что один из мальчиков оба раза солгал, а трое в каждом из своих заявлений говорили правду. Так кто же разбил вазу?
Пример 3. В симфонический оркестр приняли на работу трѐх музыкантов: Бориса, Сергея и Владимира, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
![]() Сергей самый высокий;
Сергей самый высокий;
играющий на скрипке меньше ростом играющего на флейте; играющие на скрипке и флейте и Борис любят пиццу; когда между альтистом и трубачом возникает ссора, Сергей мирит их; Борис не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Пример 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия. Пример 5. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Домашняя работа.
Пример 6. Четыре школьника, Миша (М), Коля (К), Сергей (С) и Петр (П), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:
Миша: «Я не бил окно, и Коля тоже...»
Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!» Сергей: «Я не делал этого, стекло разбил Миша».
Петр: «Я не делал этого, я выходил в этот момент в коридор».
Стало известно, что двое из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.
Кто разбил стекло в классе?
Пример 7. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.