ОСНОВЫ ЛОГИКИ. АЛГЕБРА ЛОГИКИ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

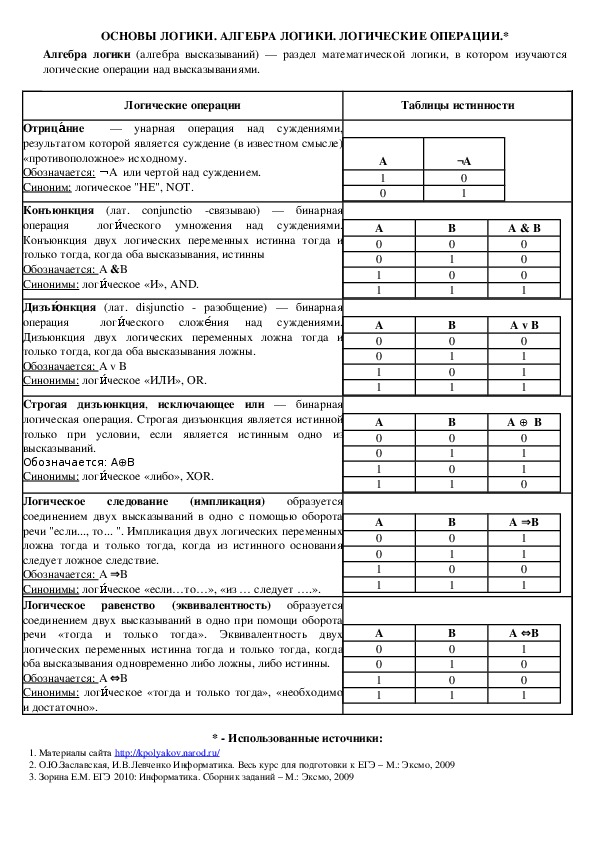
ОСНОВЫ ЛОГИКИ. АЛГЕБРА ЛОГИКИ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ.* Алгебра логики  (алгебра  высказываний)  — раздел  математической  логики, в котором изучаются логические операции над высказываниями.  Логические операции Таблицы истинности аа   Отриц ние   —   унарная   операция   над   суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному.  Обозначается: ¬А  или чертой над суждением.  Синоним: логическое "НЕ", NOT. Конъюнкция  (лат.   conjunctio   ­связываю)   —   бинарная ии   лог ческого   умножения   над   суждениями. операция   Конъюнкция   двух   логических   переменных   истинна   тогда   и только тогда, когда оба высказывания, истинны Обозначается: А &В Синонимы: лог ческое «И», AND. ии юа ии Дизъ нкция   (лат.   disjunctio   ­   разобщение)   —   бинарная   лог ческого   слож ния   над   суждениями. операция   Дизъюнкция   двух   логических   переменных   ложна   тогда   и только тогда, когда оба высказывания ложны. Обозначается: А v В Синонимы: лог ческое «ИЛИ», OR. ии еи Строгая   дизъюнкция,  исключающее   или  —   бинарная логическая операция. Строгая дизъюнкция является истинной только   при   условии,   если   является   истинным   одно   из высказываний.  Обозначается: А⊕В Синонимы: лог ческое «либо», XOR. ии ии (импликация)  Логическое   следование   образуется соединением двух высказываний в одно с помощью оборота речи "если..., то... ". Импликация двух логических переменных ложна  тогда и только  тогда,  когда из  истинного основания следует ложное следствие. Обозначается: А ⇒В Синонимы: лог ческое «если…то…», «из … следует ….». Логическое   равенство   (эквивалентность)  образуется соединением двух высказываний в одно при помощи оборота речи   «тогда   и   только   тогда». Эквивалентность   двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Обозначается: А ⇔В Синонимы:  лог ческое «тогда и только тогда», «необходимо и достаточно». ии А 1 0 А 0 0 1 1 А 0 0 1 1 А 0 0 1 1 А 0 0 1 1 А 0 0 1 1 ¬А 0 1 В 0 1 0 1 В 0 1 0 1 В 0 1 0 1 В 0 1 0 1 В 0 1 0 1 А & В 0 0 0 1 А v В 0 1 1 1 А ⊕  В 0 1 1 0 А ⇒В 1 1 0 1 А ⇔В 1 0 0 1 1. Материалы сайта http://kpolyakov.narod.ru/ 2. О.Ю.Заславская, И.В.Левченко Информатика. Весь курс для подготовки к ЕГЭ – М.: Эксмо, 2009 3. Зорина Е.М. ЕГЭ 2010: Информатика. Сборник заданий – М.: Эксмо, 2009 * ­ Использованные источники: 4. Н.Д.Угринович Информатика и ИКТ. Учебник для 10­11 классов (профильный).­ М.: БИНОМ. Лаборатория знаний, 2010