
Министерство образования Республики Башкортостан
филиал государственного автономного профессионального
образовательного учреждения Башкирский северо-западный
сельскохозяйственный колледж с .Буль-Кайпаново
Разработка открытого урока по теме:
«Объем. Вычисление объемов»
Составила и провела:Фахртдинова Л.М.
02 февраля 2018года.
с. Буль-Кайпаново,2018г
Цели:
- образовательные:
вывести формулы нахождения объемов тел, углубить и расширить знания о возможностях интегрального исчисления, сформулировать у учащихся умение находить объемы различных тел
Метод: поисковый, творческий.
Приемы: наблюдение, анализ, использование ранее приобретенных умений.
-воспитательные:
воспитание аккуратности и внимательности при записи формул и построении чертежей; формирование навыков контроля и самоконтроля; активизация познавательной деятельности в коллективе и формирование навыков сотрудничества в решении поисковых задач
развивающие:
развитие умения логически мыслить, аргументировать, доказывать;
развитие умения применять полученные знания в практике; развитие абстрактного и наглядно-образного мышления.
Метод: поисковый, творческий.
Приемы: наблюдение, анализ, использование ранее приобретенных умений.
Ход урока.
1.Организационный момент.
Выступление преподавателя об измерениях в геометрии и физике(краткая историческая информация из введения по учебнику стр.186)..
Эпиграфом нашего урока являются слова замечательного российского математика Лобачевского: «Все в природе подлежит измерению, все может быть сосчитано».
А сегодня перед нами стоит задача ,цель :узнать о понятии объем многогранника и его вычисления.
А теперь откройте тетради , запишите дату и тему урока.
2.Объяснение новой темы.
Вспомним про параллелепипед и о его объеме(со школы).
Перед обучающимися ставится задача(практическая) :определить разными способами объемы параллелепипеда и тела неправильной формы(куска пластилина):1)Один учащийся выходит к доске и измеряет размеры параллелепипеда. Другой ученик записывает результаты измерения и формулу на доске. Остальные- вычисляют в тетрадях. Вопрос :каким методом вычислили объем и что получили?(математический, положительное число).
2)вызываю одного ученика к доске для определения объема тела неправильной формы с помощью мензурки и воды. Другой ученик записывает результаты измерения на доске и вычисляет. Остальные- вычисляют в тетрадях на местах. Вопрос :каким методом вычислили объем и что получили?(физический , положительное число).
3) Существует еще один способ определения объема. Это –интеграль- ный способ.(на доске объясняю тему учебник Башмаков для НПО стр.205))
Итак, сделаем вывод: значит. что называется объемом?
Запишем определение.( Из слайдов или из учебника).
3.Закрепление изученного материала.
А теперь решим задачи из учебника (стр.207)
№17.
4. Подведение итогов урока.
Итак, мы с вами сегодня узнали и вспомнили понятие объем и его вычисления для многогранников .
Оценки за урок: …..
5.Домашнее задание .
№19(1),Выучить определения и свойства(по тетрадям).
6.Рефлексия учащихся.
На этом урок окончен. До свидания и ваши пожелания и оценка уроку : если вам урок понравился -положите красный жетон в конверт,
если нет-черный.



Объемом называется положительная величина,характеризующая часть пространства,занимаемую телом
Объем можно описать через его свойства. Они принимаются без доказательства. Поэтому являются аксиомами.
Свойства объемов(аксиомы)
•За единицу измеренияобъемов принимают объем куба с ребром ,равным единице
•Равные тела имеют равные объемы
•Если тело можно разбить на несколько простых тел, то его объем равен сумме объемов составляющих тел


 О
О
тношение объемов подобных тел равно кубу коэффициента подобия.
Объем прямоугольного параллелепипеда
•Объём прямоугольного параллелепипеда равен произведению трех его измерений.
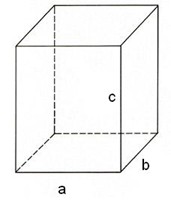

Следствия
•Объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
•Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
Объём наклонной призмы
•Объём наклонной призмы равен произведению площади основания на высоту.
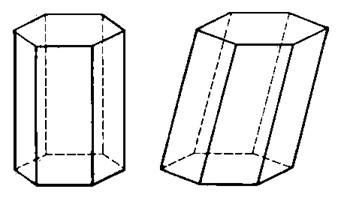

Объём пирамиды
•Объём пирамиды равен одной трети произведения основания на высоту.
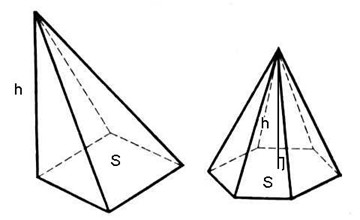

Объемы тел вращения
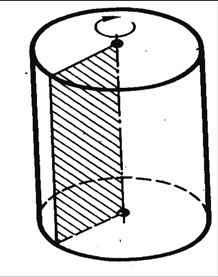
Объём цилиндра
•Объём цилиндра равен произведению площади основания на высоту.

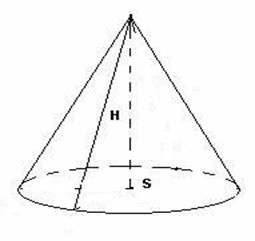
Объём конуса
•Объём конуса равен одной трети произведения площади основания на высоту.

Следствие
•Объём V усеченного конуса, высота которого равна h, а площади оснований равны S и S1,вычисляется по формуле:
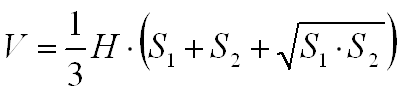
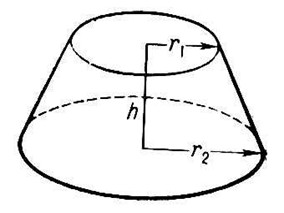
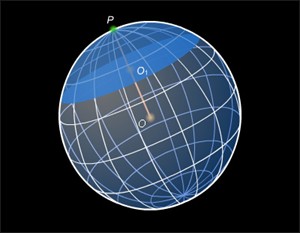
Объём шара
•Объем шара радиуса R равен:
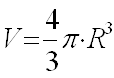
Слайд 1 |
|
Объемы тел. |
Слайд 2 |
|
Объемом называется положительная величина, характеризующая часть пространства, занимаемую телом. |
Слайд 3 |
|
Свойства объемов |
|
За единицу измерения объемов принимают объем куба с ребром, равным единице. Равные тела имеют равные объемы. Если тело можно разбить на несколько простых тел, то его объем равен сумме объемов составляющих тел Свойства объемов |
Слайд 4 |
|
Отношение объемов подобных тел равно кубу коэффициента подобия. |
Слайд 5 |
|
Объем прямоугольного параллелепипеда Объём прямоугольного параллелепипеда равен произведению трех его измерений |
Слайд 6 |
|
Следствия Объём прямоугольного параллелепипеда равен произведению площади основания на высоту Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту |
Слайд 7 |
|
Объём прямой призмы Объём прямой призмы равен произведению площади основания на высоту |
Слайд 8 |
|
Объём цилиндра Объём цилиндра равен произведению площади основания на высоту |
Слайд 9 |
|
Объём наклонной призмы Объём наклонной призмы равен произведению площади основания на высоту S h |
Слайд 10 |
|
Объём пирамиды Объём пирамиды равен одной трети произведения основания на высоту |
Слайд 11 |
|
Следствие Объём V усеченной пирамиды, высота которой равна h, а площади оснований равны S и S1, вычисляется по формуле |
Слайд 12 |
|
Объём конуса Объём конуса равен одной трети произведения площади основания на высоту |
Слайд 13 |
|
Следствие Объём V усеченного конуса, высота которого равна h, а площади оснований равны S и S1, вычисляется по формуле |
Слайд 14 |
|||||
|
|
|||||
|
Объём шара Объем шара радиуса R равен |
|||||

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.