
КГУ «Зыряновский сельскохозяйственный колледж»
Открытый урок по алгебре на тему:
Применение интеграла. Вычисление площади плоских фигур с помощью интеграла.
Преподаватель математики:
Торношенко В.А.
2016-2017 учебный год
Дисциплина: алгебра
Тема раздела: Первообразная.
Тема урока: Применение интеграла. Вычисление площади плоских фигур с помощью интеграла.
Цель урока: создать условия для формирования представления о площади криволинейной трапеции и интеграле, вывести формулу для вычисления площадей плоских фигур с помощью определенного интеграла.
Задачи:
Обучающая: сформировать навык вычисления площадей плоских фигур с помощью определенного интеграла
Развивающая: развитие внимания, речи, логического мышления, аккуратности в записи; совершенствование графической культуры.
Воспитывающая: воспитывать стремление к расширению знаний.
Оборудование: мультимедийный проектор, экран, презентация по теме, разработанная в среде Power Point.
Тип урока: комбинированный.
Ход урока
I. Организационный момент.
Поздороваться, посадить учащихся. Проверить наличие учащихся, их готовность к уроку, огласить тему и цели урока.
II. Проверка домашнего задания. Стр.20 №40
III. Актуализация опорных знаний.
Сегодня у нас один из заключительных уроков по теме “Первообразная”. На предыдущих занятиях мы изучили понятие первообразной, элементарные правила и формулы вычисления первообразных, научились находить площадь криволинейной трапеции, узнали, что такое интеграл, что великими учеными Ньютоном и Лейбницем была выведена формула, которая носит их имя, с ее помощью можно вычислять интеграл, решать задачи прикладного характера в физике, геометрии.
Как-то в шутливой форме Пафнутий Львович Чебышев высказал мысль: “В своем развитии математика прошла три периода:
- в первом – задачи ставили боги (задачи удвоения куба по древнегреческому преданию приписывались оракулу),
- во втором – полубоги (т.е. математики, такие как Ферма),
- в третьем периоде задачи ставит жизнь”.
Открытия в физике, астрономии привели к открытию интегрального и дифференциального исчисления.
Я предлагаю вам вспомнить изучаемый материал последних уроков.
Устно:
1. Какие из функций F(x) являются первообразными функции f(x). (Слайд 3)
2. Является ли данная функция первообразной для f(x)=sinx? (Слайд 4)
3. Для вычисления определенного интеграла от функции f(x)служит формула Ньютона-Лейбница. Эта знаменитая формула, одна из самых важных в математическом анализе, названа именами его основоположников. (Слайд 5)
Исаак Ньютон – физик и математик. Создал современную механику и открыл Закон Всемирного Тяготения. В его главном сочинении “Математические начала натуральной философии” дан математический вывод основных фактов о движении небесных тел. Один из создателей дифференциального и интегрального исчисления.
Готфрид Вильгельм Лейбниц (1646-1716). Немецкий математик, физик, философ, создатель Берлинской академии наук. Основоположник дифференциального и интегрального исчисления, ввел большую часть современной символики математического анализа.
А теперь поговорим о приложении, т.е. применении определенного интеграла для вычисления площадей плоских фигур.
На прошлых занятиях мы познакомились с понятием криволинейной трапеции.
- Дать определение криволинейной трапеции. (Слайд 6)
(Ответ: Фигура,ограниченная графиком непрерывной, не меняющей знака на [a;b] функции, отрезком [a;b] оси ОХ , прямыми х=a и х= b)
-Какая фигура является криволинейной трапеции. (Слайд 7)
Вспомнить алгоритм нахождения площади криволинейной трапеции. (Слайд 8)
( 1. Построить фигуру.
2. Найти пределы интегрирования.
3. Записать формулу вычисления площади через интеграл, используя 4 основных случая.
4. Вычислить интеграл, используя формулу Ньютона-Лейбница.
5.Записать ответ.)
А если фигура не является криволинейной трапецией, как найти ее площадь? Я думаю, что вы догадались, чему будет посвящен сегодняшний урок.
Запишите тему урока: “Вычисление площадей плоских фигур с помощью определенного интеграла”.
IV.  Изложение нового материала
Изложение нового материала
Пусть плоская
фигура ограниченная сверху графиком функции ![]() ,
снизу графиком функции
,
снизу графиком функции ![]() ,
слева прямой х=а, и справа прямой x= b.
,
слева прямой х=а, и справа прямой x= b.
На рисунке мы видим две криволинейные трапеции. Чтобы вычислить площадь заштрихованной фигуры, надо от площади большой криволинейной трапеции вычесть меньшей криволинейной трапеции.
 |
Пример: Найти площадь фигуры ![]() и
и ![]()
![]()
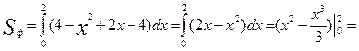 1 способ
(используем формулу):
1 способ
(используем формулу):
![]() 2 способ (от площади
прямоугольника отнимем площадь криволинейной трапеции):
2 способ (от площади
прямоугольника отнимем площадь криволинейной трапеции):
 |
|||
V. Закрепление нового материала.
Решение задач у доски стр 25 №62, 63
(индивидуальная работа по карточкам)
Выполнение теста в программе My Test
VI.Итог урока. Выставление оценок (2 мин).
Задание на дом:
1. ![]() Ответ:
1 кв. ед.
Ответ:
1 кв. ед.
2. ![]() Ответ: (32/3) кВ. ед.
Ответ: (32/3) кВ. ед.
3. ![]() Ответ: 32 кв. ед.
Ответ: 32 кв. ед.
Приложение
I. Обучающая карточка, рассчитана на слабого учащегося.
Справа - решённое задание, слева - необходимо решить аналогичную задачу.
С помощью интеграла вычисли площадь фигуры, ограниченную линиями
![]()
у= х2 и у = 4 у= х2 и у = 1
Решение: Решение:
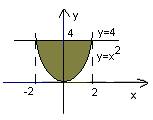
х2 = 4
х = 2 или х = -2
3.
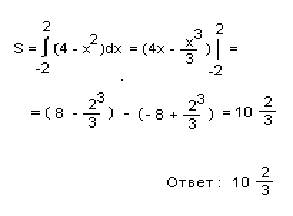
II. Карточка, рассчитана на среднего учащегося.
С помощью интеграла вычисли площадь фигуры, ограниченную линиями
![]() ,
, ![]() ,
, ![]() ,
, ![]()
III. Карточка, рассчитана на сильного учащегося.
Вычислите площадь фигуры, ограниченной графиком функции
у= 8х - 2х2, касательной к этой параболе в точке с абсциссой х=1 и прямой х=0.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.