
Открытый урок по математике в 7г классе по теме: «Линейная функция и ее график»
Цели:
Образовательные:
• обобщить и систематизировать знания и умения учащихся по теме «Линейная функция»
• развивать познавательные способности учащихся на основе упражнений
Воспитательные:
• мотивация учебной деятельности
• воспитание ответственного отношения к учению
• воспитывать интерес к урокам математики
Развивающие:
• развитие познавательного интереса, наблюдательности, устойчивого внимания, творческой активности, самостоятельности, умения сравнивать, делать выводы, развитие логического мышления
• приобретение навыков работы в парах
• расширение кругозора обучающихся, пополнение словарного запаса
• развитие речи, самостоятельности, мышления и активности
• развитие графической культуры обучающихся
• развивать межпредметные связи между математикой и другими науками
• развитие интереса к предмету
Задачи:
• закрепить такие понятия, как функция, аргумент, область определения функции, график функции
• повторить способы задания функции
• формировать у обучающихся умения находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу
• закрепить изучение линейной функции и ее частного вида — прямой пропорциональности
• развивать навык построения и чтения графиков этих функций
• добиться понимания, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b
• закрепить умение нахождения точки пересечения прямых по графику и по формулам линейных фунуций
• закрепить умение нахождения значений к и b для функций вида у=кх+b
• рассмотреть примеры реальных зависимостей между величинами дляусилению прикладной направленности курса алгебры
Оборудование: компьютер, проектор, экран; презентация (задания и правильные ответы для самопроверки), карточки-задания «Ключевое слово»
• Организационный момент Дорогие ребята, уважаемые гости, сегодня у нас обобщающий урок по теме: «Линейная функция», на котором необходимо повторить теоретический материал и применить его для решения задач
• Актуализация знаний
• Какую функцию называют прямой пропорциональностью?
• Как построить график функции y = kx?
• Как расположен в координатной плоскости график функции y = k x при k>0 и при k<0?
• Сформулируйте определение линейной функции.
• Что является графиком линейной функции?
• Как построить график линейной функции?
• Как расположен в координатной плоскости график функции y = k x +в при k>0 и при k<0?
• -в каком случае графики двух линейных функций пересекаются? Как найти координаты точки пересечения?
• -в каком случае графики двух линейных функций являются параллельными прямыми?
• Работа по теме урока
Вариант 1
1. Графиком линейной функции служит прямая линия
2. Если функция задана формулой у = kx, то она прямая пропорциональность
3. Если линейная функция задана формулой у = 1,5х + 3, то ее угловой коэффициент равен 3
4. Графики линейных функций у = 2х – 3 и у = 2х + 1 пересекаются
5. Точка А (- 3; - 2) принадлежит графику функции у = -2х +4
6. Если график функции у = kx проходит через точку А ( 2; 5 ) , то число k = 2,5
7. Графики функций у = 5х – 3 и у = 3х + 1 пересекаются в точке А( 2;7 )
Ответ: да, да, нет, нет, нет, да, да
Вариант 2
1. Если функция задана формулой у = kх + b, то она линейная
2. Чтобы построить график линейной функции, достаточно
в системе координат отметить две точки и через них провести прямую
3. Если линейная функция задана формулой у = - х + 5, то ее угловой коэффициент равен 1
4. Графики линейных функций у = - 2х + 3 и у = 2х - 5 параллельны
5. Точка В ( 2; 4 ) принадлежит графику функции у = 3х +10
6. Если график функции у = kx проходит через точку В ( - 2; 8) , то число k = - 4
7. Графики функций у = - 4х + 3 и у = 0,5х + 3 пересекаются в точке А( 0;3 ).
Ответ: да, да, нет, нет, нет, да, да
Учитель: «Поменяйтесь тетрадями и проверьте результаты тестов. Ответы на доске».
• Применение знаний и умений в новой ситуации
• Даны функции у = (2а – 1)х и у = (4а + 3)х + 2а. При каких значениях параметра а графики данных функций параллельны?
Постройте график функции:
У =
2х, если - 1? х < 1,
3 – x, если 1? x ? 4.
• Даны пять функций. Выпишите те из них, которые являются линейными
(2-3 мин на выполнение; 1 мин – на проверку)
Ответ:
Проверка осуществляется с помощью проектора, учащиеся ставят на листах у соответствующих функций «+» - верно, «-» - неверно.
Контрольный вопрос: почему функции
а) ; б) являются линейными. Указать .
Ученики ставят себе оценку за выполнение 1-го задания
2) Построить графики выписанных линейных функций
(8 мин – на выполнение, 2 мин – на проверку)
Учитель показывает графики с помощью ММП. Анализируются ошибки. Ученики оценивают свою работу.
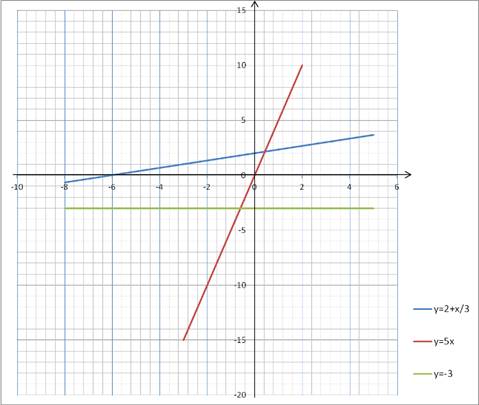
3. Выяснить, проходит ли график функции через заданную точку
3 мин – на выполнение, 1 мин – проверку
Решение:
1 вар.
С(26;8)
8=13-3
8=10 – неверное числовое равенство, след.график функции не проходит через точку С.
2 вар.
М(-42;-12)
12=2-14
- верное числовое равенство, след.график функции проходит через точку М.
Учащиеся оценивают свою работу
• Задать формулой функцию, график которой изображен на рисунке.
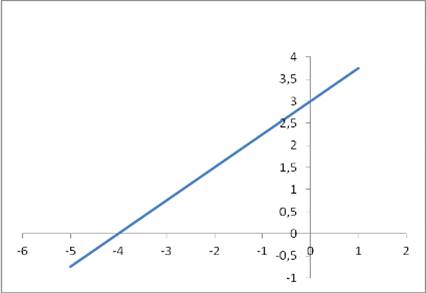
8 мин – на выполнение, 1 мин – на проверку
Решение:
1 вар.
1) b=3,
k>0
2) (-4;0) 0=k·(-4)+3
-3=k·(-4)
k=
2 вар.
1) b=2
k<0
2) (5;0) 0=k·5+2
-2=k·5
k=
• Физминутка
• Закрепление
Тествариант 1
1.Заданафункцияу= 0,5х– 6.
Найдитеу(-2) .
О. –7; А. 4; Б. –5; В. –3
2. Вкакихкоординатныхчетвертях
проходитграфикфункцииу= 2х– 1?
С. 1; Т. 1,3,4; Р. 2,3; К. 1,3
3. Графиккакойфункции - прямая,
параллельнаяосиординат?
Ф. у=6х; Л. х=-8; М. у=6; П. у=х
4. Найдитеточкупересеченияграфика
функцииу= 5х-1 сосьюабсцисс.
Е(0;2); Г(1,1); И(0,2;0); Ю(0;0,2)
5.Принадлежитлиграфикуфункции
у=0,5х-20 точкаВ (10;10)?
Ц. принадлеж.; Ч. непринадлежит
6.Задайтелинейнуюфункцию, графиккоторойпараллеленпрямойу= -0,3х-8 ипроходитчерезначалокоординат.
Д. у=х-0,3; К. у=-0,3х-6; Н. у=-0,3х
7.Вычислитекоординатыточки
пересеченияграфиковфункций:
у=х+0,5 иу=3х-5,5.
З. (-3;2,5); Г.(3;2); Ш.(3,5;3); О.(3;3,5)
Тествариант 2
1.Заданафункцияу=6х- 1. Найдитех, еслиу=5.
А. 3; Б. 7; В. -1; О. 1
2. Вкакихкоординатныхчетвертях
проходитграфикфункцииу= - 7х+9?
Г. 1,2,; Н. 1,3; С. 2,4; Т. 1,2,4
3. Графиккакойфункции–прямая,
параллельнаяосиабсцисс?
М. х=5; Д. у=х+4; Л. У=9
4. Найдитеточкупересеченияграфика
функцииу=0,5х-3 сосьюординат.
К. (-3;0); П. (0;3); И. (0;-3 ); Р. (-3;0)
5. Принадлежитлиграфикуфункции
у=-4х+1 точкаЕ (-2;9)?
Т. принадлеж.; Ч. непринадлежит
6. Задайтелинейнуюфункцию,графиккоторойпараллеленпрямойу=4х-5 ипроходитчерезначалокоординат
Ю. у=-4х; Н. у=4х; М. у= 4х+5
7. Вычислитекоординатыточки
пересеченияграфиковфункций:
у=-х-2,5 иу= 4х-7,5
• О. (1;3,5); Я. (-1;1,5); П. (-3,5;1)
6. Подведение итогов
1) Какая функция называется линейной?
2) Что является графиком линейной функции?
3) Сформулировать алгоритм построения графика линейной функции
• Домашнее задание: п. 8, № 7.17(б), 8.17(б, г), 8.46(б).
8. Рефлексия
- Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно.
- Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно.
Изучение
темы “Линейная функция” в 7 классе является начальным этапом
работы с функциональными зависимостями и на этом этапе необходимо
использовать все возможности для развития учащихся.
Основная цель при изучении данной темы — сформировать представление о
числовой функции на примере линейной функции.
Построение графика линейной функции и чтение графика — важнейшие
умения, необходимые учащимся для изучения как других разделов
математики, так и смежных дисциплин. Формирование этих умений ведется
не только при решении традиционных математических примеров, но и в
процессе моделирования реальных процессов, протекающих по закону
линейной зависимости. На данном уроке рассматривается зависимость расположения
графика функции от значений коэффициента k и в. Знания, полученные учащимися
в
процессе работы по данной теме, являются базовыми и будут использоваться
для дальнейшего изучения функций в старших классах. Специфика
проведения данного урока в том, что он частичнопоисковый при
актуализации знаний учащихся, изучении нового материала и закреплении
полученных знаний. Урок проводится в 7 классе, который по степени усвоения
учебного материала и по результативности в практической деятельности
учащихся
неоднородный, поэтому учебный материал подобран так, что задания
дифференцированы, есть индивидуальная работа учащихся. Использование
разнообразных приемов и методов: словеснологического,
наглядного, репродуктивного, частичнопоискового – помогает повысить
мотивацию к изучению математики, помогает сохранить логические связки
между этапами урока. Рациональное распределение времени между этапами урока
позволяет рассмотреть объемный материал. Для предупреждения перегрузок и
снятия психофизического напряжения учащихся, в середине урока
предусмотрена
физкультминутка. В ходе урока комплексно решаются образовательная, развивающая
и воспитательная задачи. Их полному решению способствует структура
урока.
Учитывая специфику данного урока, большую часть урока занимает
практическая работа, направленная на получение знаний и закрепление
изученного материала.
В
ходе урока осуществляется постоянный контроль качества знаний, умений и
навыков: беседы, фронтальный опрос, индивидуальная работа.
Весь урок поддерживается хорошая психологическая атмосфера. Между
учителем и учениками идет полноценное общение.
Домашнее задание не вызовет затруднения у всех учеников, потому
что аналогичные задания были разобраны на уроке.
В начале урока основной целью было быстро включить учащихся в деловой ритм, были актуализированы знания, необходимые для работы над новым материалом. Одновременно шла эффективная работа над развитием речи, мыслительных операций, о чем свидетельствовала деятельность учащихся. Для создания проблемной ситуации в начале урока был использован прием «Верите ли вы, что ..», само задание не вызвало затруднения , но проблемная ситуация мотивировала поиск нахождения ответа для изучения нового материала.
При изучении нового материала старалась, чтобы учащиеся сами анализировали задания, в результате чего, сами приходили к нужному ответу, я старалась только направлять класс, для поиска нужного результата.
В процессе первичного закрепления задания решались в форме устной работы и выполнения самостоятельной работы по вариантам с взаимопроверкой.
При работе в лабораториях ( парах) учащиеся развивали свою коммуникабельность, формировали умение работать в паре. При выполнении самостоятельной работы каждый ученик смог себя проверить, осознать: все ли он понял, запомнил, повторил построение графиков, научился делать выводы и сравнивать. Считаю, что на данном этапе каждый ученик смог пережить ситуацию успеха, убедиться, что изученный материал им освоен (или не освоен), о чем свидетельствовали результаты их самооценки.
На уроке был использован следующие формы работы: фронтальная, ндивидуальная, групповая, диалоги «ученик-ученик» и «ученик- учитель», игровая.
На этапе рефлексии учащиеся подвели итоги, получили достоверную информацию о достижении собственных планируемых результатов, оценили свои знания, увидели, что они не усвоили и над чем стоит еще поработать.
Домашнее задание задано творческое.нормативным требованиям, оно дано с комментированием.
План урока выполнен, задачи решены.Учащиеся новый материал поняли и усвоили, что подтвердили результаты самостоятельной работы.
Спасибо Сиянат Джанбековне за этот урок.
Родители 7г класса
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.