Открытый урок по математике в 8в классе по теме: «Трапеция»

Цели урока:

Ввести понятие, термин и определение «трапеции». Рассмотреть виды трапеции: произвольная, равнобедренная, прямоугольная; свойство средней линии трапеции, свойства равнобедренной трапеции и её признаки.

Развивать связную, логическую речь, наблюдательность. Учить сравнивать, обобщать, делать выводы, доказывать свои предположения и утверждения.

Воспитывать мотивацию к учению.

Оборудование: мультимедийный проектор, карточки с задачами по уровням сложности из конспекта урока.

1.     Организационный момент. Приветствие учителя и учащихся. 

Эпиграф нашего сегодняшнего урока:

Три пути ведут к знанию:  путь размышления – это путь самый благородный,

                                              путь подражания – это путь самый лёгкий и

                                               путь опыта – это путь самый горький.

                                                                                           КОНФУЦИЙ

 

2.     Актуализация знаний

Выберите верные утверждения:

Параллелограмм это четырехугольник, у которого стороны попарно равны.( да )

  Сумма углов четырехугольника 1800.( нет)

Противоположные углы параллелограмма равны .( да)

 Диагонали параллелограмма равны (нет)

 Диагонали ромба  пересекаются и точкой пересечения делятся пополам.( да)

 Параллелограмм это четырехугольник у которого стороны попарно параллельны.( да)

Квадрат  является ромбом.( да)

Диагонали прямоугольника равны.( да)

Диагонали прямоугольника пересекаются под прямым углом. ( нет)

Диагонали ромба являются биссектрисами его углов.( да)

 

На экране разноцветные четырехугольники.

• В царство каких фигур мы попали?

• Разделите фигуры на классы по какому-либо признаку.

• Дайте определение фигурам известного класса

 

 

3.     Объяснение нового материала

1. Определение трапеции и ее элементов. На экран выводится изображение трапеции. Дайте определение трапеции, опираясь на существенный признак и запишите это определение с помощью математических символов

Рассмотрим четырехугольник, про который можем сказать , что две противолежащие стороны параллельны, две другие не параллельны.

Трапеция – (от греч. trapezion, букв. – столик).

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные.

Виды трапеции.    Равнобедренная – трапеция, у которой равны боковые стороны.

Прямоугольная – трапеция, один из углов которой прямой.

 

4.      Первичное осмысление и закрепление знаний.

 

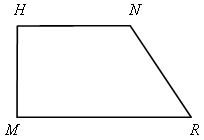
Какие четырехугольники на рисунке являются трапециями? Назовите их основания и боковые стороны.

 

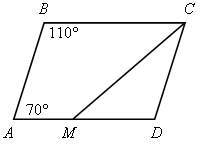
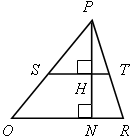
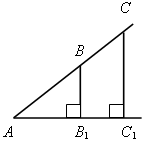
  а)                                           б)                                     в)

Какие виды трапеции бывают?

 

 

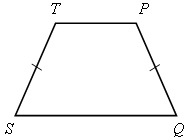
5.Закрепление изученного, решение задач

 

Задача 387. Найдите углы B и D трапеции ABCD с основанием AD и BC, еслиА=36° ,С=117°.

 

- Какие свойства  вы использовали для решения этих заданий?

 

-возможны варианты ответов;

1. В решении задач на трапецию можно использовать свойства углов при параллельных прямых и секущей 1 = 2 (как внутренние накрест лежащие при ВС || АD и секущей ВD).
2,3 + 4 = 180° (как внутренние односторонние при СD || ВЕ и секущей ВС).
3,5 + 6 (как соответственные при ОР || MR и секущей ОМ).

 

 

 

 

 

 

 

 

 

 

 

№ 388 (а).

I способ:

1) Проведем СЕ || АВ. 2) Докажем, что АВСЕ – параллелограмм, тогда АВ = СЕ. 3) Докажем, что СDЕ – равнобедренный, тогда 1 = 2. 4) Докажем, чтоА = 2. (Используя, что АВ || CЕ, А и 1 – соответственные.) 5) Докажем, чтоВ = ВСD (используя, что АD || ВС, В и А, ВСD и 2 – пары внутренних одно-сторонних углов).

II способ:

1) Проведем ВМ  АD и СН  АD. 2) Докажем, что ВСНМ – параллелограмм, тогда ВМ = ЕН. 3) Докажем, что АВМ = DСН (по катету и гипотенузе), тогда А = D. 4) Аналогично I способу докажем, что АВС = ВСD.

№ 389 (признаки равнобокой трапеции; обратная теорема № 388 (а; б).

а)	Проведем СЕ || АВ, тогдаА = = Е = D. СЕD – равнобедренный, поэтому СD = СЕ, а так как АВСZ – параллелограмм, то АВ = СЕ. Имеем АВ = СЕ = = СD. АВСD – равнобокая трапеция.
б)	АСD = DВА  по  I  признаку равенства треугольников, тогда АВ = СD.

 

6.     Самостоятельная работа

Решение задач по готовым чертежам.

 

I уровень

1. Найдите неизвестные углы трапеции:

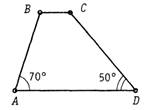
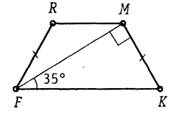
II уровень

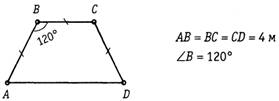
2. Найдите периметр трапеции АВСD:

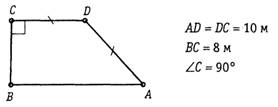
III уровень

1. Из вершины тупого угла равнобедренной трапеции АВСD проведен перпендикуляр СE к прямой AD, содержащий большее основание. Докажите, что AE=(AD+BC)/2.

2. В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей  боковой стороной угол в 60⁰. Докажите, что меньшая диагональ равна полусумме оснований трапеции.

 

7. Рефлексия:
На уроке  я узнал...

Мне было интересно, что ...

Я разобрался в том, что...

Мне стало понятно ,что...

Мне было увлекательно...

Я познакомился ...

8. Домашнее задание.

п. 59, № 61, № 62.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учащиеся были подготовлены к уроку (внешний вид учеников, их рабочая поза, состояние рабочего места). Классное помещение также было подготовлено к проведению урока. Организационный момент включал в себя приветствие учителем учащихся, проверку готовности кабинета и учащихся к уроку, проверки посещаемости.

Актуализация опорных знаний началась с устного опроса по теории. Ответы по теоретическому материалу ученики давали математически грамотные и полные. Углубление материала продолжилось других этапах урока (решение задач устно по готовым чертежам, а так же решение задач письменно на применение свойств и признаков параллельных прямых ).

    Проверка знаний учащихся проходила в форме теста. (проверка теста прошла на уроке - выполнена самими учениками.)

    Время на каждый этап урока распределено рационально. Использованы различныевиды оценки: самооценка, взаимооценка, прогностическая оценка.

    При работе в парах у учащихся формировался навык взаимоконтроля; при проверке заданий - самоконтроль и самооценка; со стороны учителя - мягкий контроль.

Проверка сформированности умений и навыков была организована в течение всего урока:
- ответы на вопросы учителя;
- фронтальный опрос; -устное решение задач по готовым чертежам
- решение задач изученных видов; -решение задач из материалов ОГЭ.
Разнообразие форм организации учебной работы:
- фронтальная;
- индивидуальная.
Создание эмоционально-благоприятной ситуации:
- игровые приемы;
Виды контроля:
- ученик - ученик
- самоконтроль
- ученик - учитель (сравнение своей работы с образцом)
На различных этапах урока применялись методы:
- словесный;
- наглядный.
Высокая работоспособность обучающихся в течение всего урока обеспечивалась за счет:
- правильной регламентации продолжительности и рационального чередования различных видов деятельности;
- использование наглядного метода обучения;
- присутствие диалога между учителем и учащимися;
- моменты переключения с одного вида деятельности на другой;
- поддержание интереса к процессу обучения через нестандартные задания, задания развивающего характера.
Психологическая атмосфера поддерживалась за счет демократического стиля общения, создания ситуации успеха для каждого ученика, стимулирование активности учащихся, что обеспечивает эмоциональный комфорт и психологическую безопасность.

    Считаем, что урок - адаптивный, так как все дети смогли реализовать свои образовательные потребности, возможности и способности. Ситуация успеха каждого ребёнка формировалась как на протяжении всего урока, так и на отдельных его этапах. В частности при выполнении тестовой работы.

Психологический настрой, движение во время проверки заданий, способствовало расслаблению детей, сохранности их здоровья.

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мы родители 8в класса, посетили открытый урок Сиянат Джанбековны. Урок был очень эмоционально-насыщенный. Материал, подобранный для урока был доступен для всех обучающихся этого класса. Дети учились определять тему урока и формулировать ближайшую учебную цель.
В результате групповой работы были выдвинуты проблемы при решении задач и дальнейшее их разрешение . Эта работа проводилась для того, чтобы обучающиеся учились добывать новые знания, находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Проверка знаний осуществлялась в ходе решения теста по вариантам. Тест проверялся в результате взаимопроверки. Проведена самооценка.
Обратная связь осуществлялась при работе с разноцветными карточками в форме четырехугольников. Ребята усвоили материал, с учетом способностей каждого ребенка, при этом не было перегрузок.На уроке были реализованы принципы наглядности, научности (дети оперировали научными понятиями), доступности (реализован в подборе материала), принцип связи обучения с жизнью.
Важным моментом также на уроке было соблюдение здоровьесберегающего  режима: смена видов деятельности, упражнения для снятия нагрузки с глаз.
Общая организация работы на уроке позволила создать в классе рабочую обстановку и рационально распределить время на каждом этапе.

Учебное время на уроке использовалось эффективно, запланированный объём урока выполнен. Интенсивность урока была оптимальной с учётом физических и психологических особенностей детей.
Итог урока был подведён. В завершении урока был проведён самоанализ деятельности учеников на уроке. Свою работу на уроке дети оценили с помощью разноцветных карточек в форме четырехугольников.

 

 

Родители8 в класса