Открытый урок по геометрии в 11 классе: Решение задач по теме «Цилиндр»

Достижения на данном уроке составляют следующие: • Закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра). • Сформировать навыки решения типовых задач. • Развивать пространственные представления на примере круглых тел. • Продолжить формирование логических и графических уменийМАОУ «Гимназия №76» Открытый урок по геометрии в 11 классе Решение задач по теме «Цилиндр» Подготовила учитель математики: Хоружая Н. А. 2015 год Тема урока: Решение задач по теме «Цилиндр» Тип урока: Обобщение и систематизация знаний учащихся. 1. Цели: • Закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра). • Сформировать навыки решения типовых задач. • Развивать пространственные представления на примере круглых тел. • Продолжить формирование логических и графических умений Форма урока: урок обобщения и систематизации знаний. Оборудование: доска,проектор, экран, компьютер, указка, карточки, на столах рабочие тетради учащихся. Задачи урока: Учебная: закрепить знания учащихся по изученной теме. Развивающая: способствовать формированию умений применять приемы: обобщения, развитию математического кругозора, мышления и речи, внимания и памяти. Воспитательная: – содействовать воспитанию интереса к математике, активности, умения общаться, общей культуры. План урока. № Этап урока Цель и содержание этапов Деятельность учащихся 1. Организационный момент. Мотивация Приветствие. Проверка готовности к уроку. Постановка цели урока. Целеполагание. Отвечают на приветствие. 2. Вступление к уроку. Объяснение этапов урока. Повторение ранее изученного материала Работа по карточкам 3. Обобщение и систематизация знаний Организация деятельности учащихся: решение задач, обучающая самостоятельная работа Учащиеся работают по карточкам, отвечают устно, работают в тетрадях тетрадях, выполняют самостоятельную работу 4. Информация о домашнем задании Дать информацию о домашнем задании и комментарии к его выполнению Запись домашнего задания 5. Рефлексия, выставление оценок Анализ, оценка и коррекция знаний учащихся Ход урока 1. Организационный момент. 2. Повторение ранее изученного материала. Учащимся предлагается заполнить лист с заданиями. Возможен вариант работы с применением копировки (в таком случае один экземпляр сдается учителю, а второй ребенок проверяет в ходе дальнейшей работы на уроке). Карточка. 1. Нанесите на рисунок основные элементы цилиндра. 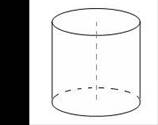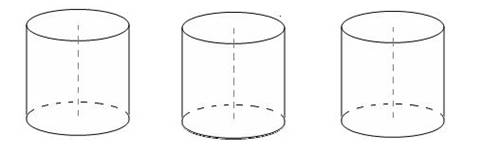2.Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае? 3. Запишите формулы для вычисления площади поверхности цилиндра. Что можно найти по этим формулам? Что должно быть известно в этих случаях? Учащиеся сдают листы с заданием. Фронтальный опрос (с целью обобщения знаний и проверки выполненной работы) • Какая фигура называется цилиндром? Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов. • Почему цилиндр называют телом вращения? Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон. • Назовите виды цилиндров? Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности • Назовите элементы цилиндра. Основания цилиндра – равные круги, расположенные в параллельных плоскостях Высота цилиндра - это расстояние между плоскостями его оснований. Радиус цилиндра – это радиус его основания. Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра). Образующая цилиндра - это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра. Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра. • Что представляет собой развертка цилиндра? Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания. • Как найти площадь боковой поверхности цилиндра? Sб = H · C = 2πRH • Как найти площадь полной поверхности цилиндра? Sп = Sб + 2S = 2πR(R + H). • Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае? Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники Сечение плоскостью, параллельной оси цилиндра. В сечении – прямоугольники. Сечение плоскостью перпендикулярной оси цилиндра. В сечении круги, равные основанию. • Приведите примеры использования цилиндров. Цилиндрическая гастрономия. Цилиндрическая архитектура. Цилиндры фараона 3. Закрепление материала. Решение задач. Ученики видят список задач для классной работы. По желанию учащиеся имеют возможность решать с опережением на оценку. 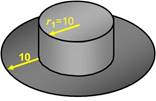№1. (задача с практическим содержанием). Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. №2 (523). Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра. №3 (525). Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра. №4 (527). Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13. №5* (532). Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен j. 4. Обучающая самостоятельная работа Самостоятельная работа по вариантам. (Возможна организация парной работы). 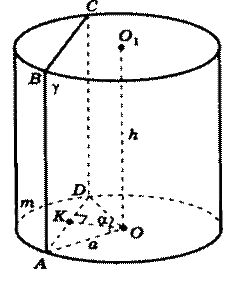Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d. 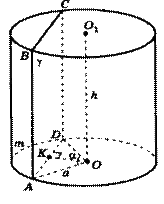Вариант 1. 1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник. 2) Найдите AD, если a =10 см, a = 60°. Вариант 2. 1) Составьте план вычисления площади сечения по данным a, h, d. 2) Найдите AD, если a =8 см, a = 120°. 5. Подведение итогов урока. 1) Домашнее задание. Повторить стр.130-132, гл. 1, п.59-60, №530, № 537. 2) Выставление оценок за работу на уроке. 3) Рефлексия. • Что нового вы узнали на уроке? • Чему вы научились? • Какое у вас настроение в конце урока? • Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня? Обучающая самостоятельная работа Вариант 1. Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d. 1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник. 2) Найдите AD, если a =10 см, a = 60°. Обучающая самостоятельная работа Вариант 2. 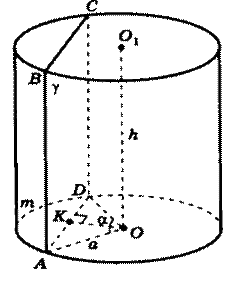Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d. 1) Составьте план вычисления площади сечения по данным a, h, d. 2) Найдите AD, если a =8 см, a = 120°.