Памятка для учителей по созданию своих заданий

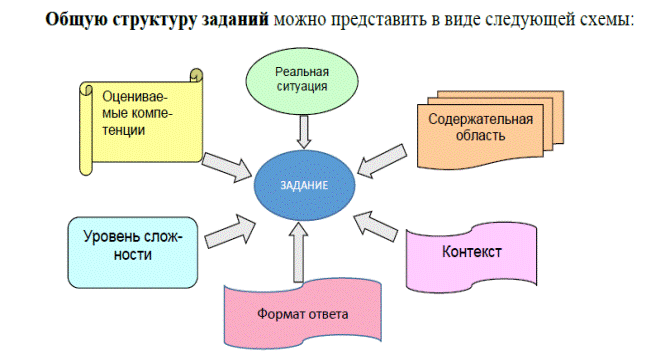
Контекст задания – это особенности и элементы окружающей обстановки, представленные в задании в рамках предлагаемой ситуации. Эти ситуации связаны с разнообразными аспектами окружающей жизни и требуют для своего решения большей или меньшей математизации.

4 основных контекста:

                общественная жизнь (обмен валюты, денежные вклады в банке, прогноз итогов выборов, демография);

                личная жизнь (повседневные дела: покупки, приготовление пищи, игры, здоровье и др.);

                образование/профессиональная деятельность (школьная жизнь и трудовая деятельность, включают такие действия, как измерения, подсчёты стоимости, заказ материалов, например, для построения книжных полок в кабинете математики, оплата счетов и др.);

                научная деятельность (рассмотрение теоретических вопросов, например, анализ половозрастных пирамид населения, или решение чисто математических задач, например, применение неравенства треугольника).

Содержательная область (математическое содержание)

заданий распределяется по четырём основным категориям:

                пространство и форма (задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу);

                изменение и зависимости (задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом);

                количество (задания, связанные с числами и отношениями между ними, т.е. с арифметикой);

                неопределённость и данные (задания, связанные с вероятностными и статистическими явлениями и зависимостями, т.е. с разделами статистики и теории вероятностей); которые охватывают основные типы проблем, возникающих при взаимодействиях с повседневными явлениями.

Для описания мыслительной деятельности при разрешении предложенных проблем используются следующие глаголы: формулировать, применять, интерпретировать и рассуждать, которые указывают на мыслительные задачи, которые будут решаться учащимися.

Оцениваемые математические компетенции (+ объект оценки) можно представить в виде следующего кодификатора.

Кодификатор умений и компетенций, характеризующих математическую грамотность учащихся

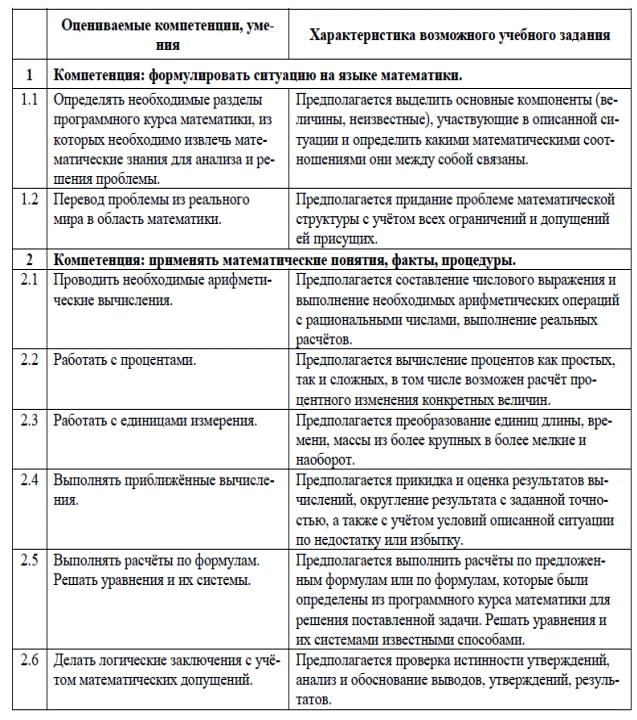
Уровни сложности:

      Низкий – выполнять одношаговую процедуру, например, распознавать ма-тематические факты, термины, методы, принципы и понятия; или найти единственную точку, содержащую информацию на графике или в таблице; производить вычисления.

      Средний – устанавливать связи и интегрировать материал из различных математических тем, необходимого для решения поставленной проблемы (использовать и применять понятийное знание для описания проблемы, выбирать соответствующие процедуры, предполагающие два шага или более); интерпретировать или использовать простые наборы данных в виде таблиц или графиков.

      Высокий – анализировать сложную информацию или данные, обобщать или оценивать доказательства, обосновывать, формулировать выводы, учитывая разные источники информации, разрабатывать план или последовательность шагов, ведущих к решению проблемы.

Форматы ответа заданий могут быть следующие:

      с выбором одного правильного ответа;

      с выбором нескольких правильных ответов;

      с кратким ответом в виде числа, буквы, числовой или буквенной последовательности, величины, слова или словосочетания;

      с развёрнутым ответом, содержащим запись решения поставленной проблемы, построение заданного геометрического объекта, объяснение полученного результата.

Выполнение заданий с выбором ответа и свободным кратким ответом оценивается автоматически (по заранее заданным ключам, либо автоматизировано, если тестирование происходит в компьютерной форме) в 1 балл, задания со свободным полным ответом оцениваются экспертами по заранее разработанным критериям оценки. Они должны включать модели ответов для каждого задания, отдельные комментарии и примеры.

Алгоритм разработки заданий

1) Отбор сюжетов, подходящих и интересных по возрасту.

2) Выявление различных ситуаций в рамках сюжета, их сути, акцентов, ограничений и возможностей математики для разрешения обозначенных проблем.

3) Выбор содержательной области (одной или несколько).

4) Описание ситуации, подбор графического материала, иллюстраций.

5) Прикидка умений (соотнесение с кодификатором умений и компетенций).

6) Составление вопросов в соответствии с кодификатором и рубрикатором, классом.

7) Конкретизация и уточнение проверяемых умений (по каждому вопросу).

8) Уточнение ситуации (в том числе, с точки зрения достаточности и необходимости информации).

9) Определение всех характеристик вопросов: содержательной области, контекста, основной мыслительной деятельности (математической компетенции), объекта оценивания (умения, согласно кодификатору), уровня сложности, формы ответа, системы оценивания.

10) Редактирование текста и наглядных материалов

В результате реализации данного алгоритма будет получен проект задания, с которым необходимо обязательно провести следующую работу:

1) провести внутреннюю экспертизу: предметную и тестологическую;

2) провести первичную апробацию, например, в виде когнитивной лаборатории;

3) провести редактирование задания по результатам первичной апробации;

4) провести внешнюю экспертную экспертизу;

5) по возможности, провести основную апробацию на более многочисленной выборке учащихся и сделать соответствующие коррективы .