
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА ИРКУТСКА СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №69
(МАОУ г. Иркутска СОШ №69)
План-конспект урока математики по теме «Функции» 9 класс
Автор:
Афанасьева Мария Николаевна учитель математики
первой квалификационной категории
Иркутск, 2023
Тема урока: «Функции»
Тип урока: интегрированный урок отработки умений и рефлексии
Вид урока: смешанный Цели урока:
1. Обобщение и систематизация знаний, полученных в 7-9 –х классах при изучении различных видов функций, их свойств.
2. Отработка
и рефлексия умений строить график линейной функции, обратной
пропорциональности, квадратичной функции и функции вида у=![]() , умений
распознавать функции по их изображению в нестандартных ситуациях.
, умений
распознавать функции по их изображению в нестандартных ситуациях.
3. Демонстрация возможности интегрирования предметов алгебра и информатика на примере построения графика кусочно- заданной функции.
Задачи урока:
1. Образовательные (формирование познавательных УУД): продолжать формировать умение обобщать и систематизировать знания по теме урока, логично и последовательно излагать материал, применять знания для выполнения практических заданий в нестандартной ситуации, заданий ОГЭ;
2. Развивающие (формирование регулятивных УУД): продолжать развивать способность самоконтроля и самоанализа учебной деятельности; умение проектировать маршрут обучения, планировать время на выполнение учебных задач, анализировать, сравнивать, обобщать, делать выводы;
3. Воспитательные (формирование коммуникативных и личностных УУД): продолжать воспитывать умение слушать и вступать в диалог при работе в группе, участвовать в коллективном обсуждении проблемы, строить продуктивное взаимодействие со сверстниками; воспитывать ответственность за результат, честность, аккуратность.
Планируемые результаты:
1. Предметные: учащийся научится воспроизводить приобретенные знания, навыки в конкретной деятельности и в новых условиях для решения практических задач; расширит представление о практическом применении графиков функций.
2. Метапредметные: учащийся получит возможность сравнивать, обобщать и проводить аналогию, интерпретировать результат в другой ситуации; оценивать правильность выполнения учебной задачи; работать индивидуально и в группе; находить общее решение.
3. Личностные: учащийся получит возможность научиться правильно излагать свои мысли, понимать смысл поставленной задачи; излагать и аргументировать свою точку зрения; оценивать себя и своих одноклассников; представить математику, как науку, присутствующую во многих сферах человеческой деятельности.
Форма организации деятельности учащихся: индивидуальная-онлайн-обучение, работа в группах, фронтальная работа с учителем
Методы обучения: словесный-диалогический, практический, наглядный
Педагогические технологии: технология смешанного обучения «Ротация станций»
Межпредметные связи: информатика Материально-техническое обеспечение содержания урока:
Технические средства: планшетные компьютеры с выходом в интернет, мультимедийное оборудование;
Методические средства: раздаточный материал, инструкции по выполнению работ, правила работы в группе
План урока:
1. Организационный этап (1 мин)
2. Мотивационный этап (2 мин)
3. Актуализация знаний (4 мин)
4. Обобщение и систематизация знаний (36 мин)
5. Рефлексия (2 мин)
1.Организационный этап
Дидактические задачи: подготовка к уроку; ведение в урок
Деятельность учителя: учитель создает комфортную рабочую обстановку, приветствует учащихся
Деятельность учащихся: учащиеся проверяют готовность рабочего места к уроку, настраиваются на успешную работу, приветствуют учителя
Ведущий метод: словесный
Форма работы: фронтальная
2.Мотивационный этап
Дидактические задачи: обеспечение мотивации и принятия учащимися цели урока, побуждение к деятельности
Деятельность учителя: организует работу по определению целей урока, обращает внимание на актуальность темы
ОДА ФУНКЦИИ
|
На первый взгляд, понятие не ново, И не всегда подумаешь о том, Как важно будет в жизни это слово И сколько смысла будет в слове том! Его по-разному с годами толковали. Сам Лобачевский руку приложил,
|
Чтоб слово «функция» и в средней школе знали, Чтоб каждый ученик им дорожил! Без функции не сдашь простой экзамен, Без функции ты не войдешь в предмет! Без функции не разгорится пламя! Без функций никакой науки нет! И. Кушнир, Л. Финкельштейн |
Деятельность учащихся: обсуждают и формулируют тему и цели урока
Ведущий метод: проблемный
Форма работы: фронтальная
3.Актуализация знаний
Дидактические задачи: анализ содержания учебного материала; подготовка учащихся к основному этапу урока
Деятельность учителя: выслушивает вопросы по домашней работе, выясняет какие трудности возникли; комментирует результаты самостоятельной работы, организует разделение учащихся на группы
Деятельность учащихся: задают вопросы по домашнему заданию, делают выводы и заключения почему возникли трудности; рассаживаются по станциям
Ведущий метод: словесный
Форма работы: фронтальная
4.Обобщение и систематизация знаний
Дидактические задачи: установление внутрипредметных и межпредметных связей; включение в практическую деятельность
Деятельность учителя: организует деятельность учащихся по включению знаний в целостную систему: работа на станциях
Деятельность учащихся: учащиеся систематизируют, обобщают знания, учатся применять их в нестандартных ситуациях; устанавливают межпредметное взаимодействие алгебры и информатики; учатся коммуницировать при работе в группах.
Ведущий метод: диалогический
Форма работы: индивидуальная, работа с учителем, работа в группе
|
Станции |
Работа с учителем
|
Работа в группе
|
Онлайн –работа |
|
деятельность учителя и учащихся |
учитель -работает с учащимися на предмет коррекции знаний по теме урока и исправления допущенных ошибок; -способствует эффективной отработке умений по теме урока за счет разноуровневых заданий (ПРИЛОЖЕНИЕ 1). учащиеся -коммуницируют с учителем на предмет возникающих вопросов по теме; |
учащиеся -знакомятся с правилами работы в группе (ПРИЛОЖЕНИЕ 2); - просматривают предложенные задания, читают инструкцию к заданию, выбирают то, с которым будут работать (ПРИЛОЖЕНИЕ 3); -выполняют выбранное задание; -сверяют с эталоном (в зависимости от |
учащиеся -знакомятся с инструкцией по построению графиков функций в EXCEL (ПРИЛОЖЕНИЕ 5)- ссылка на инструкцию находится на рабочем столе планшета; - выбирают из предложенных ту функцию, график которой будут |
|
|
-отрабатывают умения и навыки по теме, выполняя практические задания. Оборудование: карточки с разноуровневыми заданиями (ПРИЛОЖЕНИЕ 1) |
выбранного уровня сложности) (ПРИЛОЖЕНИЕ 4) Оборудование: раздаточный разноуровневый материал (ПРИЛОЖЕНИЕ 3), разлинованные в клетку листы формата А4. |
строить (ПРИЛОЖЕНИЕ 3); -приступают к построению графика; -сверяют с эталоном (ПРИЛОЖЕНИЕ 6) Оборудование: планшетный компьютер, разноуровневые задания (ПРИЛОЖЕНИЕ 3) |
|
12 мин (по истечению переходят на другую станцию) |
1-я группа
|
2-я группа
|
3-я группа
|
|
12 мин(по истечению переходят на другую станцию) |
3-я группа |
1-я группа |
2-я группа |
|
12 мин(по истечение остаются на своих места) |
2-я группа |
3-я группа |
1-я группа |
5.Рефлексия
Дидактические задачи: сделать выводы по уроку, получить обратную связь от учащихся
Деятельность учителя: проводит оценку уровня решения учебной задачи, просит проанализировать учащихся свою работу и ответить на вопрос «Достигнута ли цель урока?», информирует о домашнем задании
Деятельность учащихся: оценивают уровень собственных достижений, записывают домашнее задание
Ведущий метод: диалогический
Форма работы: фронтальная, индивидуальная
ПРИЛОЖЕНИЕ 1
Задания 1-го уровня сложности:
1. График какой из приведенных ниже функций изображен на рисунке?
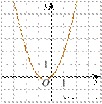
![]() 1)
1)
2.График какой из приведенных ниже функций изображен на рисунке?
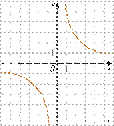
1) ![]() 3)
3) ![]() 4)
4)
![]()
3.Установите соответствие между графиками функций и формулами, которые их задают.
А) Б) В)
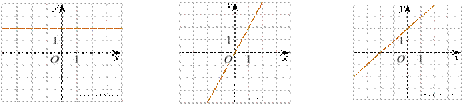
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
|
А |
Б |
В |
|
|
|
|
4. Установите соответствие между функциями и их графиками.
А) ![]()
Графики
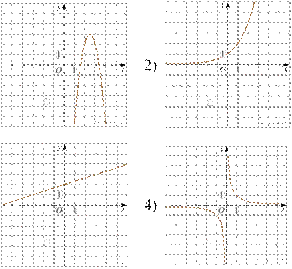 1)
1)
3)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
|
|
|
|
5. Установите соответствие между функциями и их графиками.
А) ![]() Б)
Б) ![]() В)
В) ![]()
Графики
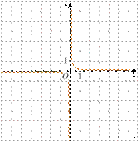
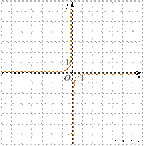 1) 2)
1) 2)
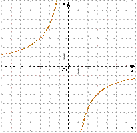
3) 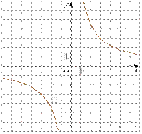 4)
4) 
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
|
|
|
|
6. Установите соответствие между функциями и их графиками.
Функции
А) ![]() Б) В)
Б) В)
Графики
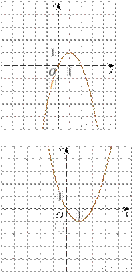 1)
1) 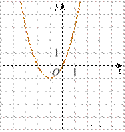 2)
2)
3) 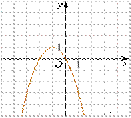 4)
4)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
|
|
|
|
7. Постройте в одной системе координат графики функций на заданной области определения: у1=-х+25, если 3≤ х ≤ 10 у2=0,25х2, если -2≤ х ≤ 2
![]() , если -4≤
х < 10
, если -4≤
х < 10
Задания 2-го уровня сложности (дополнительные к заданиям 1-го уровня сложности):
1.На одном из рисунков изображен график функции у=х𝟐-2х+3. Укажите номер этого рисунка.

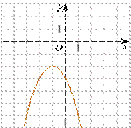 1) 2)
1) 2)
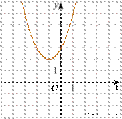
3) 4)
2.На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c.
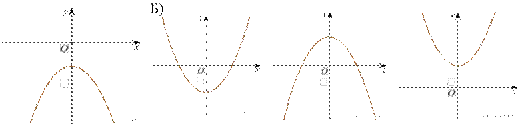 А) В) Г)
А) В) Г)
Знаки коэффициентов
1) a > 0, c < 0 2) a < 0, c > 0 3) a > 0, c > 0 4) a < 0, c < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
|
|
|
|
|
3.На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
А) Б) В)
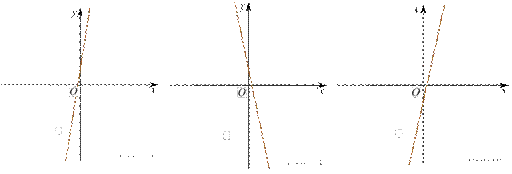
1) k < 0, b > 0 2) k > 0, b > 0 3) k < 0, b < 0 4) k > 0, b < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
|
|
|
|
4. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты
|
А) a > 0, c < 0
|
Б) a < 0, c > 0 Графики |
В) a > 0, c > 0 |
|
1) |
2) |
|
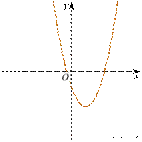
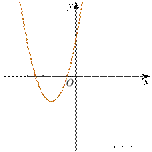
4)
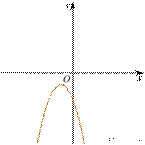 3)
3)
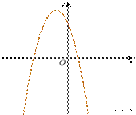
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
|
|
|
|
5.Постройте график функции и определите, при каких значениях прямая у=с имеет с графиком ровно две общие точки, опишите свойства функции:
2х + 1, если х < 0
У={−1,5х + 1, если 0 ≤ х < 2 х − 4, если х ≥ 2
СВОЙСТВА ФУНКЦИЙ:
1.Область определения
2.Область значений
3.Нули функции
4.Промежутки возрастания/убывания
6.Промежутки знакопостоянства
7.Непрерывность
8.Четность/нечетность
Задания 3-го уровня сложности (дополнительные к заданиям 1-го и 2-го уровней сложности):
1.Постройте
график функции у=![]() и опишите свойства функции.
и опишите свойства функции.
СВОЙСТВА ФУНКЦИЙ:
1.Область определения
2.Область значений
3.Нули функции
4.Промежутки возрастания/убывания
6.Промежутки знакопостоянства
7.Непрерывность
8.Четность/нечетность
2.Первая прямая проходит через точки (0;4,5) и (3;6) Вторая прямая проходит через точки (1;2) и (-4;7) Найдите координаты общей точки этих двух прямых.
3.
Постройте график функции у=![]() и определите, при каких значениях k
построенный график не будет иметь общих точек с прямой y=kx.
и определите, при каких значениях k
построенный график не будет иметь общих точек с прямой y=kx.
ПРИЛОЖЕНИЕ 2
Станция «Работа в группе»
1. Длительность работы в группе-12 минут.
2. Внимательно изучите предложенные задания. Изучите инструкции к заданию (если они есть).
3. Выберите задание, суть которого вам наиболее понятна и с которым вы сможете справиться за отведенное время.
4. Обсудите задание в группе. Проанализируйте на предмет возможных затруднений.
5. Определите роли в группе. Выберете выступающего или выступающих от группы.
Определите его (их) задачи.
6. Приступайте к выполнению задания.
7. Таймер оповестит вас об окончании работы.
ПРИ ВОЗНИКНОВЕНИИ ЗАТРУДНЕНИЙ ОБРАТИТЕСЬ ЗА ПОМОЩЬЮ К УЧИТЕЛЮ
ПОМНИТЕ:
• Работайте в группе дружно- вы одна команда.
• Принимайте активное участие в обсуждениях.
• Не бойтесь высказывать свое мнение.
• Не старайтесь всех перекричать. Уважайте мнение других участников группы.
• Каждый человек имеет право на ошибку.
ПРИЛОЖЕНИЕ 3
 2.КОРАБЛИК
(1-й /2-й уровни сложности) Постройте график функции
2.КОРАБЛИК
(1-й /2-й уровни сложности) Постройте график функции
РЕКОМЕНДАЦИИ: для более быстрого построения графика функции выбирайте «конечные» абсциссы из предложенного интервала. При необходимости возьмите дополнительные абсциссы из этого же интервала.
|
3.ВАЗА С ЦВЕТАМИ (3-й уровень сложности) Постройте график функции
РЕКОМЕНДАЦИИ: для более быстрого построения графика функции выбирайте «конечные» абсциссы из предложенного интервала. При необходимости возьмите дополнительные абсциссы из этого же интервала.
|
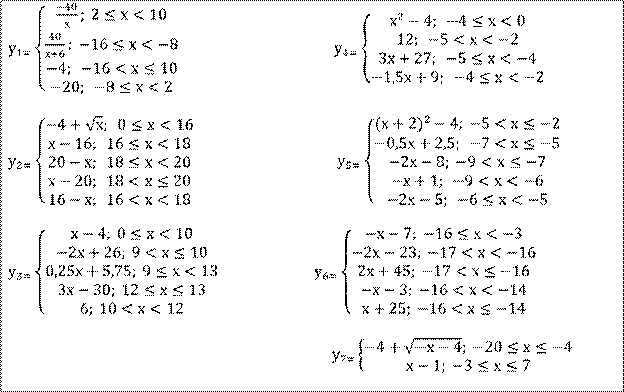
ПРИЛОЖЕНИЕ 4
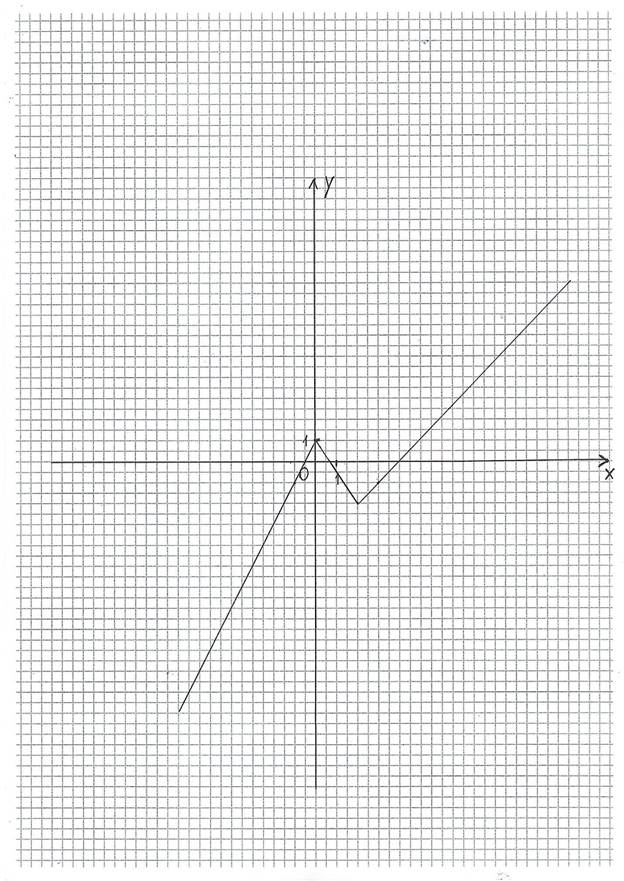
РИС.1
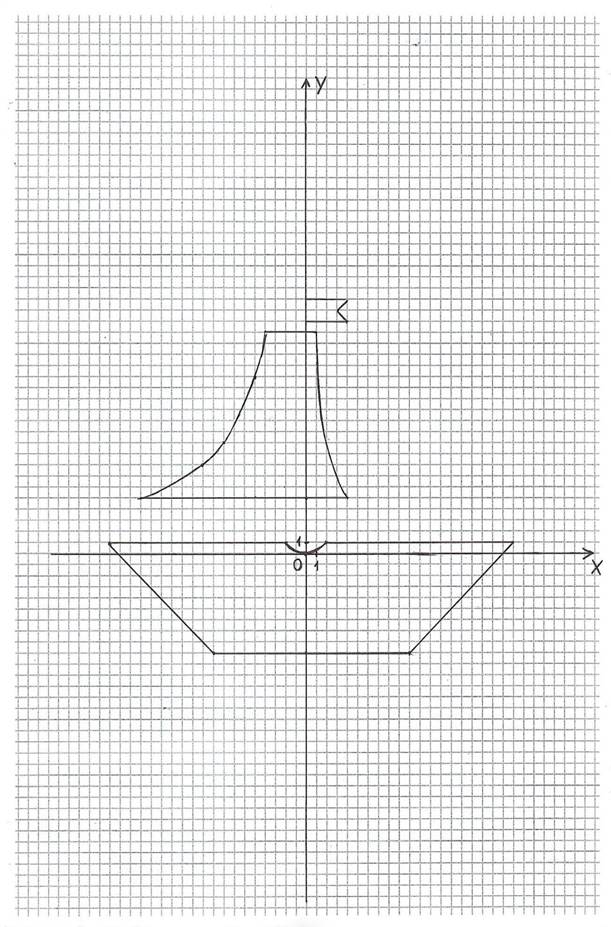
РИС.2
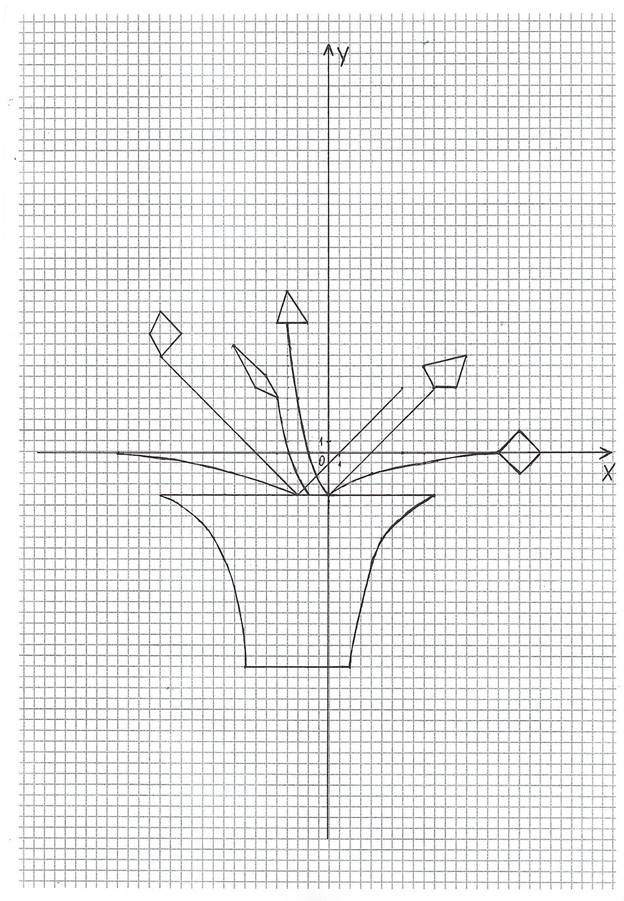
РИС. 3
ПРИЛОЖЕНИЕ 5
Станция «Онлайн-работа»
(https://docs.google.com/document/d/1Io4U-
EuUgjXIbOWGeTQ_XodDGqoVU1u03qKXsDowZsg/edit?usp=share_link)
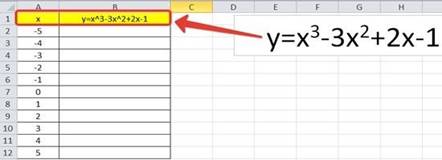
Пример 1
Дана функция: у=х𝟑-3х𝟐+2х-1
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
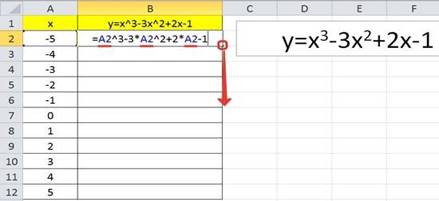
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8). Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
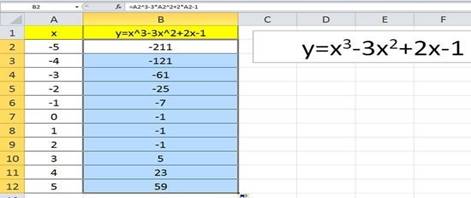
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом
1.
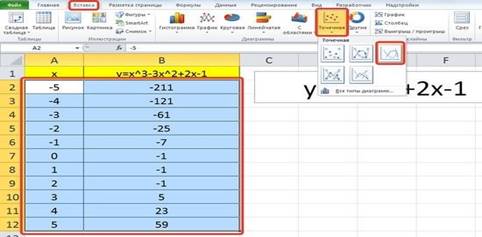
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
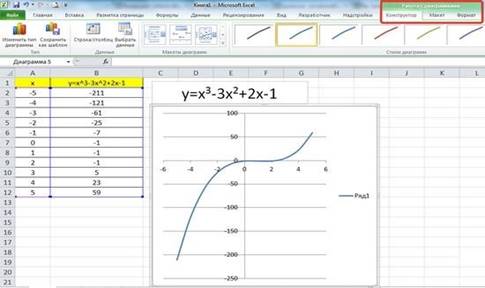
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции: у=х𝟑-3х𝟐+2х-1 и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
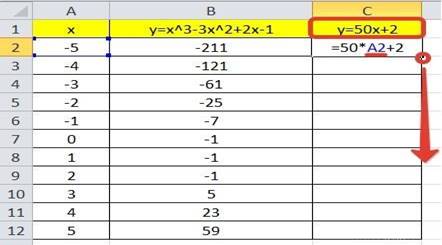
Мы получили таблицу значений переменной х и обеих функций в этих точках.
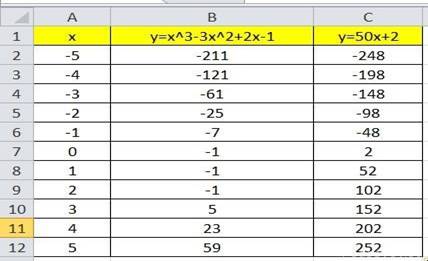
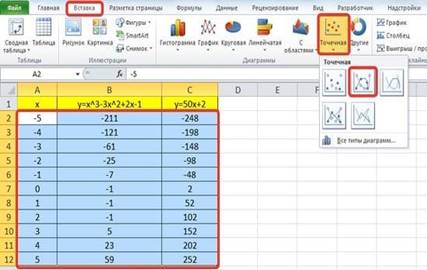
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
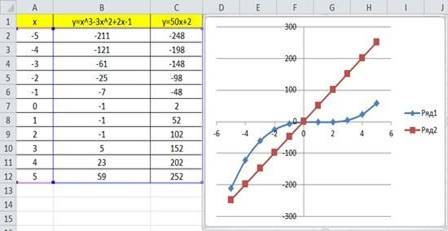
ПРИЛОЖЕНИЕ 6
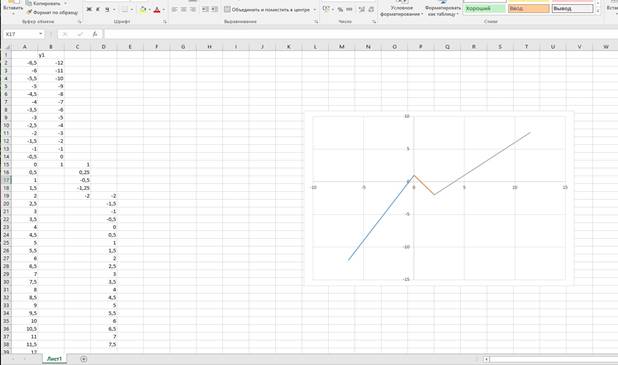
РИС.4
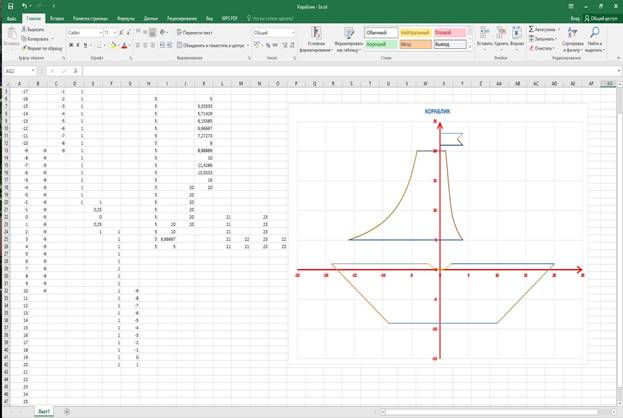
РИС.5
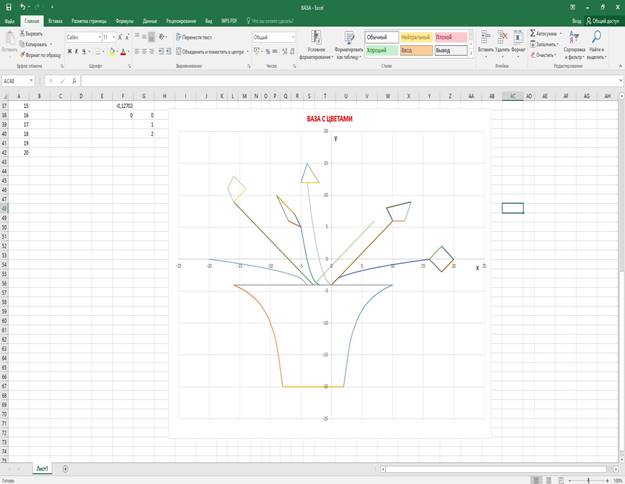
РИС.6
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.