План-конспект урока по английскому языку на тему: " Целое уравнение" 9 класс

 

 

 

 

 

 

 

 

 

 

 

 

Урок алгебры в 9 классе

Тема урока: «Целые уравнения»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок алгебры в 9 классе

Тема урока: «Целые уравнения»

 

Основная цель урока: способствовать формированию представления о понятии «целое уравнение», дать понятие целого уравнения и его степени, познакомить со способами  решения целых уравнений.

Задачи урока:

1.Образовательные: закрепить, систематизировать знания, умения и навыки решения целых уравнений первой, второй и третьей степени, актуализировать опорные знания решения квадратных уравнений.

2.Развивающие: развивать умения в применении знаний в конкретной ситуации; логическое мышление, умение работать в проблемной ситуации; умение обобщать, конкретизировать, правильно излагать мысли; развивать самостоятельную деятельность учащихся.

3.  Воспитательные: воспитывать интерес к предмету через содержание учебного материала; умение работать в коллективе, взаимопомощь, культуру общения, умение применять преемственность в изучении отдельных тем; воспитывать настойчивость в достижении цели, умение не растеряться в проблемных ситуациях

Оборудование:  ПК, мультимедийные проектор, интерактивная доска, пульты

Приложение: Презентация к уроку в программе PowerPoint

Ход урока.

I.  Организационный момент. Сообщение темы, целей урока.

II. Устная работа.

Повторение: 1) целое выражение и его степень (привести примеры). ПК, мультимедийные проектор

1) х² – 2х;                            

2) х² + 6х + 9;

3) 3a⁴ – 9a⁴;                         

4) а² – 10а + 25;

5) т² -  4п;                           

6) а³ – 7а;     

7) 

                       

8) (x + 1)(x - 2)

9)

10)

11)

Привести примеры дробных выражений. Указать степень многочлена.

2) 1) Что такое уравнение? (Равенство, содержащее переменную, называется уравнением с одной переменной)

2) Что такое корни уравнения? (Значение переменной, при котором уравнение обращается в верное числовое  равенство )

3) Какие из чисел -3; -2; -1; 0; 1; 2; 3 являются корнями уравнения:  х³ -9х =0

Что значит решить уравнение? (Найти все его корни или доказать, что корней нет)

х + 2,3 = 7     х = - 4,    х = 4,7 (какое из чисел является корнем уравнения?)

  III. Объяснение нового материала

  1)Определение целого уравнения.

   Уравнения, в которых левая и правая часть являются целыми выражениями, называются целыми уравнениями.

2) Определите степень уравнения: Уравнения бывают 1, 2, 3, 4, и более высоких степеней. Мы с вами большей частью решаем уравнение I, II, III IV степени.

Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль. 

       Если уравнение с одной переменной записано в виде P(x) = 0, где P(x)- многочлен стандартного вида, то степень этого многочлена называют степенью данного уравнения

    

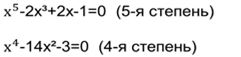
Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль. 

      Степенью произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)- многочлен стандартного вида  

x (x – 1)= 0        у²(у- 4)=0         

х² - х=0            у3-4у²=0

Закрепление понятия степени уравнения

Укажите степень уравнения

(выполняют устно, при необходимости записать в тетрадь № 5,9,10)

1) x² = 0                           6) x² –16 = 0    

2) x³ – 25x = 0                 7) x⁴ – 3x² = 0

3) 9x –27 = 0                     8) x² = – 49

4) 10 – х² = 26х                   9) x(x – 1)(x + 4) = 0

5) x (6 - x )(x - 9)=0          10) (x² – 25 ) х - x³ = 0

 

3)Примеры решения уравнений различных степеней:

1.Уравнение первой степени можно привести к виду ax+b=0, где х – переменная, a и b – некоторые числа, причём при a≠0. Из уравнения ax+b=0, при a≠0 получаем, что   – корень уравнения. Каждое уравнение первой степени имеет один корень.

2х + 3 = 0     

  х = 4,    х = - 3,       х = 0 (являются ли корнями данного уравнения?)

    2. Уравнения второй степени можно привести к виду ax²+bx+c=0, где х – переменная, a, b и c – некоторые числа, причём при a   ≠  0. Число корней такого уравнения зависит от дискриминанта  D=b²–4ac

    Решите уравнения:  (1чел. с каждого ряда, на месте 1 ряд 1 уравнение, 2 ряд- 2 уравнение, 3 ряд- 3 уравнение)

I вариант       II вариант      III вариант   (рассмотреть 2 способа решения  x²-12x+36=(х-6)²)

x²-5x+6=0      y²-4y+7=0         x²-12x+36=0

D=1, D>0,      D=-12, D<0      D=0,1 корень 

    x₁=2, x₂=3      нет корней       x=6.                      

  Сколько корней может иметь уравнение  2  степени (квадратное)?  Не более двух!

   3. Уравнение третьей степени можно привести к виду ax³+bx²+cx+d=0,

     уравнение четвёртой степени – к виду ax⁴+bx³+cx²+dx+e=0, и т. д.,  где a, b, c, ... – некоторые числа, причём при a≠0

Динамическая пауза. ПК, проектор, гимнастика для глаз.

IV. Закрепление изученного материала.

Решение уравнений, применяя разложение на множители.

Пример 1: Вынесение  множителя за скобки.

  у³-4у²=0,

    у²(у-4)=0.

    у=0 или у-4=0,

                   у=4.

Ответ:0 и 4.

            Разложение на множители способом группировки.

Пример 2. 3х³+х²+18х+6=0,   

               х²(3х+1)+6(3х+1)=0,

               (3х+1)(х²+6)=0,

              3х+1=0 или х²+6=0,

             х=-⅓            х²=-6,корней нет.     

            Ответ: -⅓.

Пример 3.  (8x-1)(2x-3)-(4x-1)²=38

                   16x²-24x-2x+3-16x²+8x-1-38=0

                  -18x-36=0

                  -18x = 36

                  x=-2

                       Ответ:  -2

Решить № 267 (б) рассмотреть 2 способа решения: умножение на общий знаменатель и с помощью пропорции.

Пример 4.  x³–8x²–x+8=0.

                                         

 

 

 

 

 

           х=8     х=1     х=-1

Ответ: -1,1,8

V.  Итог урока.

Вопросы учащимся: Какое уравнение называется целым? Как найти степень целого уравнения? Сколько корней имеет целое уравнение в зависимости от степени уравнения?

 

Обучающая самостоятельная работа.

(Работа с пультами, программа Mimio Studio)

Определить степень уравнения (ученики указывают степень уравнения пользуясь пультами)

Вариант 1                                       Вариант 2

1) 3x² = 0                                  1) 3x – 5x² = 0

2) x (x – 1)= 0                           2) 2 x (x + 7) = 0

3) 7x² – 5х = 0                           3) (x – 1)(x - 2) = 0

4) 6x³ – 9x² = 0                          4) x (6 - x )(x - 9)

5) х(x -2) +х = 0,8                     5) x² = 0,8

6) х(x – 1)(x - 2) = 0                  6) x² – 0,01 = 0,03x³

7) (x² – 25 ) х² = 0                     7) x²(x +3)(x - 9) = 0

8) 7х⁵ –5х⁴ +2 = х;                  8) 6х + 6х⁴ –3х ⁵ +1= 12

Ответы:

1)  2            2)  2          3)  3           4)  3             5)  2         6)  3              7)  4                 8)  5

Результаты работы (в процентах высвечиваются на доске), анализ ошибок.

Домашнее задание: п.12(пример 1-2) решить  № 265, 266(а),272 (а,в,д,)