План урока «Понятие последовательности. Сходящиеся последовательности. Предел последовательности»

План урока по дисциплине «Математика» специальность250109, 2 курс, 24С  группа. Тема:

«Понятие последовательности. Сходящиеся последовательности. Предел последовательности»

 

 

Дата проведения ­­­­­­­­­­­­­­­­­­______________                                                       урок№_______________

Цели урока:

Познакомить с понятием последовательность. сходящейся последовательности, пределом.

Задачи

обеспечить в ходе урока усвоение следующих основных понятий последовательность, предел последовательности

развивать мотивационные качества учащихся, мотивы учебной,
деятельности;

содействовать трудовому воспитанию учащихся;

Тип урока: 

Комбинированный урок

Методы:

репредуктивные

Межпредметные связи:.

физика «Зависимость между величинами»

Оборудование:

Доска.

Базовый учебник:  

В.П Омельченко «Математика»

  1.Организационный момент.

Отметка отсутствующих и опоздавших.

  2. Опрос

Опрос: Фронтальный устный.

1)      Дайте определение множества, величина, интервалы, функции.

2)      Что такое область определения функции?

3)      Дать понятие сложной функции.

  3. Изучение нового материала.

Дать понятия:

1)      Понятие последовательности.

2)      Сходящиеся последовательности.

3)      Предел последовательности.

4)      Число е.

5)      Бесконечно большие последовательности.

6)      Основные теоремы о пределах последовательности.

7)      Предел функции.

8)      Бесконечно большие и бесконечно малые функции.

9)      Основные теоремы о пределах функций.

10)  Замечательные пределы.

 4. Задание на дом и подведение итогов.

В.П Омельченко «Математика» стр 47-85

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Основные понятия и определения

Определение

Последовательностью называется функция, которая переводит множество натуральных чисел  в некоторое множество  : 

Элемент  называется первым членом последовательности,  - вторым, ... ,  - -ым или общим членом последовательности.

Пример

Задание. Для последовательности  определить, чему равен третий член 

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для заданной последовательности имеем, что 

Ответ. 

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Пример

Задание. Найти формулу общего члена последовательности 

Решение. Запишем каждый член последовательности в следующем виде:

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

Ответ. Формула общего члена: 

Пример

Задание. Найти 15 член последовательности, заданной формулой -го члена: 

Решение. Для того чтобы найти  , подставим в формулу общего члена значение  . Получим:

Ответ. 

Пример

Задание. Проверить, являются ли числа  и  членами последовательности

Решение. Число  является членом последовательности  , если существует такой номер  , что  :

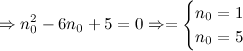
Таким образом, число  является первым и пятым членами заданной последовательности.

Проверим теперь, является ли число  членом указанной последовательности  . Рассуждая аналогично, как и для  , получаем:

Таким образом, уравнение  не имеет решение в натуральных числах, а значит, не является членом последовательности 

Ответ. Число  является первым и пятым членами заданной последовательности, а  не является членом последовательности 

Рекуррентный способ задания последовательности

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член  последовательности и известно, что  , то есть  и так далее до нужного члена.

Пример

Примером рекуррентно заданной последовательности является последовательность чисел Фибоначчи - 1, 1, 2, 3, 5, 8, 13, ... , в которой каждое последующее число, начиная с третьего, является суммой двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:

Пример

Задание. Последовательность  задана при помощи рекуррентного соотношения  . Выписать несколько первых членов этой последовательности.

Решение. Найдем третий член заданной последовательности:

Аналогично находим далее, что

и так далее

Предел числовой последовательности

Определение

Последовательность  называется сходящейся, если существует такое число  такое, что последовательность  является бесконечно малой последовательностью.

Определение

Число  называется пределом последовательности  и обозначается ,

 

Число  называется пределом последовательности  , если для любого  существует номер такой, что для любого  выполняется неравенство  :

Определение

Целой частью  некоторого числа  называется наибольшее целое число, не превосходящее 

Пример

Задание. Найти целую часть чисел - 2,36; 2,36; 2.

Решение. 

Пример

Задание. Доказать равенство: 

Доказательство. Исходя из определения, 0 будет пределом последовательности  , если для любого найдется такой номер , что для любого  выполняется неравенство :

В качестве  возьмем 

Итак, для любого  указано соответствующее значение  , а тогда равенство доказано.

Сходящиеся и расходящиеся последовательности

Определение

Последовательность, которая имеет предел, называется сходящейся; иначе - расходящейся.

Пример

Задание. Доказать, что последовательность  не имеет предел.

Доказательство. Пусть  - предел рассматриваемой последовательности, то есть . Рассмотрим 

Пусть  :

Пусть  :

Так как полученные выражения не равны, то данная последовательность предела не имеет.

Постоянная последовательность  имеет предел, равный числу  : 

Теорема

Сходящаяся последовательность имеет только один предел.

 

Теорема

(Необходимый признак сходимости последовательности).

Сходящаяся последовательность ограничена.

Последовательность на бесконечности

Последовательность  имеет бесконечный предел, если для любого 

Последовательность  называется бесконечно малой, если 

Последовательность  называется бесконечно большой, если для любого  существует номер  такое, что для любого 

Теорема

Пусть  , тогда

а)  ;

б)  ;

в) если  , то начиная с некоторого номера заданная последовательность 

 

Число е

Число e выражается через предел следующим образом: Это число является трансцендентным и приблизительно равно 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Выполнив подстановку , где , получим альтернативную формулу для данного предела: Здесь мы имеем дело со степенными выражениями, когда и основание и степень стремятся к числу a (или к бесконечности). Во многих случаях такие пределы удобно вычислять, предварительно логарифмируя функцию под знаком предела.

Пример 1

Вычислить предел . Решение.

Пример 2

Вычислить предел . Решение. Учитывая, что предел произведения нескольких функций равен произведению пределов от этих функций, получаем

Пример 3

Вычислить предел . Решение. Сделаем замену: , так что x = 6y и y → ∞, если x → ∞. В результате получаем

Пример 4

Вычислить предел . Решение.

Пример 5

Вычислить предел . Решение. Сначала преобразуем основание функции:        Введем новую переменную: . Если , то  и        В результате замены получаем

Пример 6

Вычислить предел . Решение. Предварительно преобразуем основание:        Пусть . Тогда        Теперь можно найти предел:

Пример 7

Вычислить предел . Решение. Преобразуем предел следующим образом:        Сделаем замену:        Здесь y → 0 когда x → ∞. Тогда предел равен

Пример 8

Найти предел . Решение. Пусть . Легко видеть, что  при . Тогда        Сделаем еще одну замену:        Следовательно, предел равен:

Пример 9

Найти предел . Решение. Данный предел можно представить в следующей форме:        После взятия логарифма получаем        Заметим, что . Кроме того,  при , поэтому предельный переход  во втором пределе можно заменить на . Это приводит к следующему выражению:        Учитывая, что , получаем        Следовательно, .

Пример 10

Найти предел . Решение. Перепишем предел в следующем виде:        Прологарифмируем левую и правую части полученного выражения.        Видно, что . Тогда второй предел равен e. В результате получаем        Окончательный ответ: . Предел функции Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию. Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε. Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности  такой, что  сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A. График 1.3.6.1. Предел функции y = x2 при x → 2. График 1.3.6.2. Предел функции  при x → 0. Если A – предел функции в точке a, то пишут, что  Определения предела функции по Коши и по Гейне эквивалентны. График 1.3.6.3. Предел функции y = {x (x ≠ 0); 1 (x = 0)} приx → 0 равен 0. Предел функции  в точке a = 0 равен 0:  Предел функции  в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль). Предел функции  в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1. Если функция f (x) имеет предел в точке a, то этот предел единственный. Число A1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех  выполняется неравенство   Число A2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех  выполняется неравенство   Предел слева обозначается  предел справа –  Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называютодносторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль:  и . Так, для функции  Если для каждого ε > 0 существует такая δ-окрестность точки a, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x)| > ε, то говорят, что функция f (x) имеет в точке a бесконечный предел:  Так, функция  имеет в точке x = 0 бесконечный предел  Часто различают пределы, равные +∞ и –∞. Так,  Если для каждого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство |f (x) – A| < ε, то говорят, что предел функции f (x) при x, стремящемся к плюс бесконечности, равен A:  Аналогично формулируется определение предела при x, стремящемся к минус бесконечности:  В качестве примера приведем функцию  которая стремится на бесконечности к нулю:  Наконец, запись  означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись  означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε. Если функция f (x) имеет конечный предел в точке a, то существует окрестность точки a, в которой функция f ограничена ( возможно, что в самой точке a функция не определена). При этом, если A ≠ 0, то найдется окрестность точки a, в которой (быть может, за исключением самой точки a) значения функции f имеют тот же знак, что и число A. Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, выполняются неравенства  g (x) ≤ f (x) ≤ h (x), и если   , то существует  Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, справедливо неравенство  f (x) < g (x), и если   то A ≤ B. Если функции f (x) и g (x) имеют конечные пределы в точке a, причем   то  ,  если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a. Из существования пределов f (x) в точке a и g (y) в точке f (a) следует существование предела сложной функции g (f (x)) в точке a. Для вычисления пределов часто используют так называемые замечательные пределы:

Таблица пределов функций

Держите эту таблицу основных пределов перед глазами при решении задач и примеров. Она значительно упростит Вам жизнь.

Пример.

Вычислить предел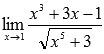 

Решение.

Подставляем значение:

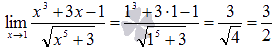
И сразу получили ответ.

Ответ:

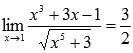
Пример.

Вычислить предел 

Решение.

Подставляем значение х=0 в основание нашей показательно степенной функции:

То есть, предел можно переписать в виде

Теперь займемся показателем. Это есть степенная функция . Обратимся к таблице пределов для степенных функций с отрицательным показателем. Оттуда имеем  и , следовательно, можно записать .

Исходя из этого, наш предел запишется в виде:

Вновь обращаемся к таблице пределов, но уже для показательных функций с основанием большем единицы, откуда имеем:

Ответ:

 

Пределы функций. Примеры решений

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.    

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:

1) Всем известного значка предела . 
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .

Сама запись  читается так: «предел функции  при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , …. 
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Готово.

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое ? Это тот случай, когда  неограниченно возрастает, то есть: сначала , потом , потом , затем  и так далее до бесконечности.

А что в это время происходит с функцией ? 
, , , …

Итак: если , то функция  стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию   бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать  до бесконечности, и смотрим на поведение функции:

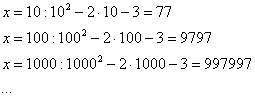
Вывод: при  функция   неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , , 
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность  , , . Если , то  , , .

Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , ,  и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.

Пределы с неопределенностью вида  и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример:

Вычислить предел 

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим  в старшей степени:

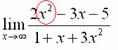
Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим  в старшей степени:

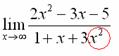
Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Разделим числитель и знаменатель на 

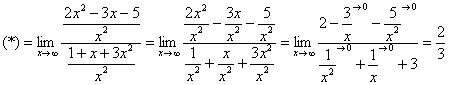
Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

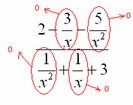
Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 2

Найти предел 
Снова в числителе и знаменателе находим  в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности  делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на 

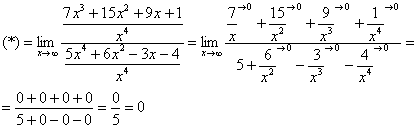
Пример 3

Найти предел 
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности  необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

Разделим числитель и знаменатель на 

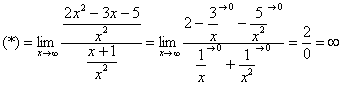
Под записью  подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида  у нас может получитьсяконечное число, ноль или бесконечность.

Пределы с неопределенностью вида  и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел 
Сначала попробуем подставить -1 в дробь:
 
В данном случае получена так называемая неопределенность .

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницуМатематические формулы и таблицы и ознакомьтесь с методическим материаломГорячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

В случае если дискриминант большой, например 361,  используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни: 

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель  уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.

Пример 5

Вычислить предел 

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Числитель: 
Знаменатель:



, 

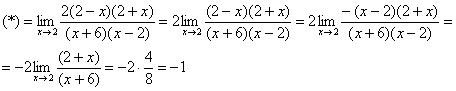
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно 
В ходе решения фрагмент типа  встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида 

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Пример 6

Найти предел 

Начинаем решать.

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

 

Получена неопределенность вида , которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности  используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов: 
И смотрим на наш предел: 
Что можно сказать?  у нас в числителе уже есть. Теперь для применения формулы осталось организовать  (которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Хорошо,  мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :

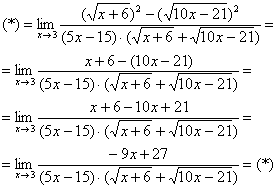
Неопределенность  не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

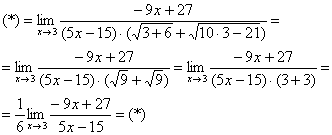
Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.

Готово.

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

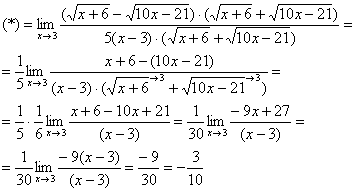
Пример 7

Найти предел 

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

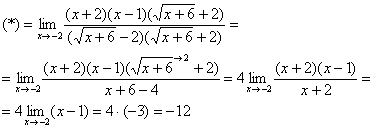
Порядок роста функции

В данном параграфе будут разобраны пределы с многочленами, многочленами под корнем, когда  или . Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!

Вычислим следующий предел: 

На базовом уроке Пределы. Примеры решений я рекомендовал рассуждать не совсем корректным способом: сначала «икс» равно 10, потом, 100, затем 1000, миллион и т.д. до бесконечности. В чём изъян такого подхода? Построим данную последовательность:

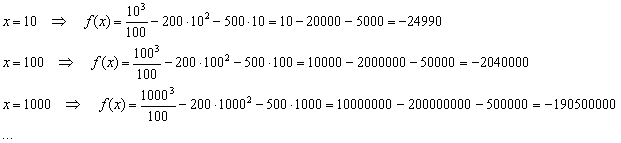
Исходя из полученных результатов, складывается стойкое впечатление, что предел стремится к «минус бесконечности»:

Но на поверку впечатление кардинально ошибочно. В этой связи необходимо знать теорию матана, а именно, некоторые выкладки о порядке роста функции.  

Применительно к нашему примеру можно сказать, что слагаемое  обладает более высоким порядком роста, чем сумма . Иными словами, при достаточно больших значениях «икс» слагаемое  «перетянет» на «плюс бесконечность» всё остальное:

При небольших значениях «икс» – да, сладкая парочка  перетягивает канат в сторону «минус бесконечности», что и привело нас к неверному первоначальному выводу. Но уже при  получается гигантское положительное число .

Если сильно уменьшить первое слагаемое, то от этого ничего не изменится: , будет лишь отсрочен тот момент, когда бравая дробь  «вытянет» весь предел на «плюс бесконечность». Не поможет и «усиление противовеса»: 
. 
Нулей можете приписать, сколько хотите (без шуток). Удивительная наука математический анализ – способна низвести любого монстра до мелочи пузатой. 

Таким образом, кубическая функция имеет более высокий порядок роста, чем:

– квадратичная функция;
– линейная функция;
– функция-константа;
– сумма квадратичной функции, линейной функции и константы (в любых комбинациях).

На простейшем примере поясню геометрический смысл вышесказанного. Представьте графики линейной , квадратичной  и кубической  функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола  взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.

Аналогичное правило можно сформулировать для любой степени:

Степенная функция данной степени растёт быстрее, чем любая степенная функция более низкой степени. И быстрее, чем сумма любого количества степенных функций более низкой степени.

Найдём предел 

Значение данного предела зависит только от слагаемого . Всё остальное МЫСЛЕННО отбрасываем: , и теперь ясно как день, что предел стремится к «минус бесконечности»:

То есть, слагаемое  более высокого порядка роста, чем всё остальное.

У «хвоста»  могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ.

Сравнение бесконечно больших функций

На первом уроке мы вычислили три предела с неопределённостью :

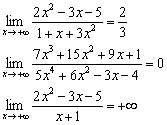
В перечисленных примерах используется стандартный приём деления числителя и знаменателя на «икс» в старшей степени и всё расписывается подробно. Но правильный ответ легко выяснить ещё до решения!

В первом примере  в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:
.

В таких случаях говорят, что функции числителя и знаменателя обладают одинаковым порядком роста. Или короче – числитель и знаменатель одного порядка роста. Действительно, в данном пределе и вверху, и внизу находятся квадратичные функции. Мир, равенство, братство.

Во втором примере  аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:

Здесь знаменатель более высокого порядка, чем числитель. Многочлен 4-ой степени растёт быстрее кубической функции и «перетягивает» предел на ноль.

И, наконец, в пределе  карлики тоже идут лесом:

А в этом примере всё наоборот – числитель более высокого порядка, чем знаменатель. Квадратичная функция растёт быстрее линейной и «перетягивает» предел на «плюс бесконечность».

Сделаем краткую теоретическую выжимку. Рассмотрим две произвольные функции , которые определены на бесконечности.

1) Если , где  – ненулевая константа, то функции имеют одинаковый порядок роста. Если , то функции называют эквивалентными на бесконечности.

2) Если , то функция  более высокого порядка роста, чем .

3) Если , то функция  более высокого порядка роста, чем .

Пример 1

Найти предел 

В наличии неопределённость  и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени.

Старшая степень числителя равна двум. Знаменатель…. Как определить старшую степень, если многочлен под корнем? МЫСЛЕННО отбрасываем все слагаемые, кроме самого старшего: . Константу тоже отбрасываем и выясняем старшую степень знаменателя: . Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля.

Почему бы сразу не узнать ответ? В числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые: . Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.

Оформляем решение:

Разделим числитель и знаменатель на 

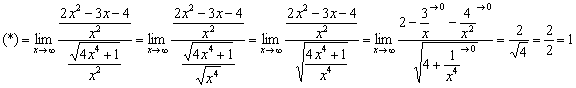
В действительности пару шагов можно пропустить, просто я подробно расписал, как в знаменателе под корень вносится .

Пример 8

Разделим числитель и знаменатель на :

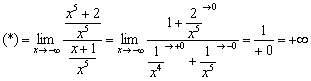
Примечание: слагаемое  стремиться к нулю медленнее, чем , поэтому  является «главным» нулём знаменателя.

Пример 10

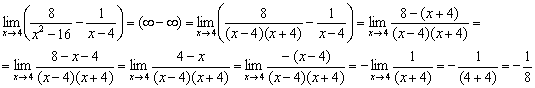
Пример 12

Умножим и разделим на сопряженное выражение:

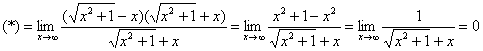
Пример 13

Умножим и разделим на сопряженное выражение:

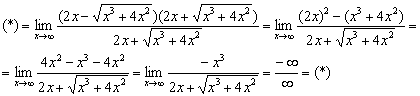
Разделим числитель и знаменатель на :

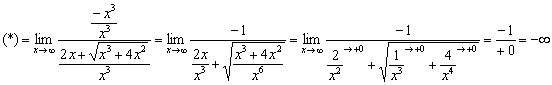
Пример 15

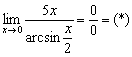
Проведём замену: 
Если , то .

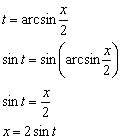
Пример 17

Проведём замену: 
Если , то .
Далее используем формулу приведения , тригонометрическую формулу  и  первый замечательный предел:

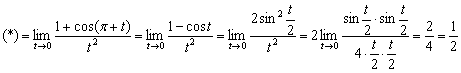
Пример 20

Используем формулу 

Пример 22

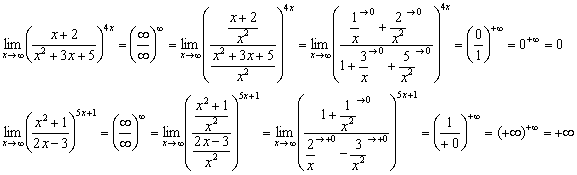
Примечание: бесконечно малая функция  стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую  роль: 

 

Скачано с www.znanio.ru