Площадь поверхности пирамиды
Цель:
-повторить определение призмы, ее элементов, вывести формулы площади боковой поверхности пирамиды, продолжить формирование навыков решения задач;
-обеспечить в ходе урока воспитания трудолюбия, самостоятельности в поисках и выборе пути решения;
-развивать познавательный интерес, пространственное воображение, геометрическое мышление, умение анализировать и сравнивать
Ход урока
1. Организационный момент. Эмоциональный настрой.
2. Мотивация урока.
Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать. Галилео Галилей.
Решить анаграммы:
Амертео (Теорема)
Мскаиоа (Аксиома)
Чкота (Точка)
Ямрпая (Прямая)
Опслькотс (Плоскость)
3. Актуализация опорных знаний. Проверка д/з.
1. Скажите, из каких фигур состоит поверхность
пирамиды?
(4 треугольника и 1 квадрат)
2. Как вы думаете, как найти площадь поверхности
данной пирамиды?
(ответы обучающихся)
3. Все вы правы, ваши предположения подходят для
любой пирамиды. Давайте подумает, как это возможно записать с помощью формулы
(ответы обучающиеся)
4. Как найти площадь боковой поверхности
пирамиды?
(найти площадь каждого треугольника и все их
сложить)
5. Как найти площадь основания?
(Узнать какая фигура находится в основании, и
найти ее площадь)
6. Как найти площадь полной поверхности
пирамиды?
(сложить полученные величины)
7. Как вы думаете, площадь правильной пирамиды
будет находиться также?
( да или нет и почему)
4. Изучение нового материала.
Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки в свою очередь позаимствовали это слово из египетского языка. В папирусе Ахмеса встречается слово «пирамис» в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от формы хлебцев в Древней Греции («пирос» - рожь). В связи с тем, что форма пламени напоминает образ пирамиды, некоторые ученые считали, что термин происходит от греческого слова «пир» - огонь. В Древнем Египте гробницы фараонов имели форму пирамид.
Начнём с определения.
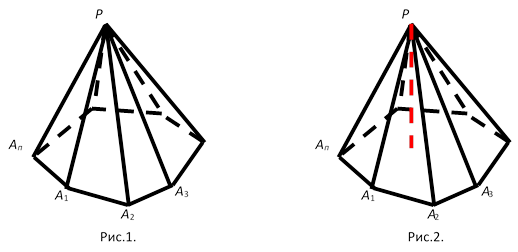Рассмотрим многоугольник A1A2…An.
Возьмем точку Р, не лежащую в плоскости этого многоугольника. Соединим
точку Р с вершинами многоугольника. Получим n
треугольников PA1A2,
PA2A3,…,
PAnA1.
(учитель проговаривает одновременно с построением чертежа).
Многогранник, составленный из n-угольника A1A2…An и n треугольников PA1A2, PA2A3,…, PAnA1, называется пирамидой. Треугольная пирамида называется тетраэдром.
Итак, что мы знаем о пирамиде?
Пирамида обозначается большими латинскими буквами, начиная с точки Р: PA1A2…An.
|
Учитель проговаривает: |
Название элемента и его обозначение для данной пирамиды |
|
Многоугольник, с которого мы начинали построение пирамиды, называется основанием. |
Основание – A1A2…An. |
|
Точка, которую выбирали вне плоскости многоугольника, называется вершиной пирамиды. |
Вершина пирамиды – P. |
|
Отрезки, которые соединяют вершину пирамиды с вершинами основания, называются боковыми ребрами |
Боковые ребра – PA1, PA2, PA3, …, PAп. |
|
Образовавшиеся треугольники – боковые грани пирамиды. |
Боковые грани пирамиды – PA1A2, PA2A3,…, PAnA1. |
Проведём из вершины пирамиды перпендикуляр к плоскости основания – PH (учитель дополняет чертеж). Он называется высотой пирамиды. Запишите еще один элемент пирамиды.
Высота пирамиды – PH.
Площадь полной поверхности пирамиды
равна сумме площади основания и площади боковой поверхности. 
,
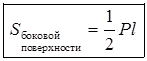где Р – периметр основания; l – апофема правильной пирамиды.
Объем пирамиды равен одной трети произведения площади основания на высоту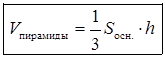 
.
5. Гимнастика для глаз
1. Вертикальные движения глаз вверх - вниз.
2. Горизонтальное движение вправо-влево
3. Вращение глазами по часовой стрелке и против.
4. Закрыть глаза и представить по очереди цвета радуги как можно отчетливее
5. Глазами нарисовать кривую, изображенную на доске, несколько раз, сначала в одном, затем в другом направлении.
6. Закрепление нового материала.
7. Самостоятельная работа. Тест
|
1.Определение пирамиды |
1. Многогранник, составленный из двух п-угольников и п-треугольников. 2. Многогранник, составленный из двух равных п-угольников, расположенных в параллельных плоскостях, и п параллелограммов. 3. Многогранник, составленный из одного п-угольника и п-треугольников. 4. Многогранник, составленный из двух равных п-угольников и п-треугольников. |
|
2.Что представляет собой боковая грань пирамиды? |
1. Параллелограмм 2. Круг 3. Прямоугольник 4. Треугольник |
|
3. Определение апофемы. |
1. Высота грани пирамиды. 2. Высота боковой грани правильной пирамиды. 3. Высота боковой грани пирамиды. 4. Высота грани правильной пирамиды. |
|
4. Определение правильной пирамиды. |
1.Прямая пирамида называется правильной, если в основании лежит правильный многоугольник. 2. Пирамида называется правильной, если в основании лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. 3. Пирамида называется правильной, если отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. 4. Пирамида называется правильной, если в основании лежит многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. |
|
5. Сколько боковых граней имеет треугольная пирамида? |
1. Одну. 2. Две. 3. Три. 4. Много. |
|
6.Площадь боковой поверхности правильной пирамиды. |
1. S=рh 2. S=2πр 3. S=πr 4.
S= |
|
7. Площадь полной поверхности пирамиды. |
1. 2Sбок.+ Sосн. 2. 2Sбок.+ 2Sосн. 3. Sбок.+ Sосн. 4. Sбок.+ 2Sосн. |
|
8. Что представляет собой боковая грань правильной пирамиды? |
1.Равносторонний треугольник 2.Квадрат 3. Прямоугольник 4.Равнобедренный треугольник |
|
9. Какая фигура не может быть в основании пирамиды? |
1. Трапеция 2. Круг. 3. Треугольник. 4. Квадрат. |
|
10. Сколько оснований имеет правильная пирамида? |
1. Одно. 2. Два. 3. Три. 4. Много. |
8. Итоги урока. Рефлексия .Д/з.
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (одним предложением).
Вам для этого помогут слова:
-Я узнал…
-Я почувствовал…
-Я увидел…
-Я сначала испугался, а потом…
Повторить п.____, решить №________. Творческое задание: подобрать или придумать задачу с практическим содержанием по теме «Пирамида».
Площадь поверхности пирамиды
В Древнем Египте гробницы фараонов имели форму пирамид
Площадь полной поверхности пирамиды равна сумме площади основания и площади боковой поверхности
Определение правильной пирамиды
© ООО «Знанио»
С вами с 2009 года.
