Площади четырёхугольников и треугольников.

Раздел:

8.3А Площади

ФИО педагога

Черепанова Валентина Валентиновна

Дата:

3 четверть

 Класс: 8

 Количество

присутствующих: ___

Количество

отсутствующих:  ___

Тема урока (2-ой урок из серии 3-х последовательных уроков)

Площади четырёхугольников и треугольников.

Цели обучения в соответствии
с учебной программой

8.1.3.13 выводить и применять формулы площади трапеции;

Цели урока

- записывает формулу площади трапеции

- применяет формулу площади трапеции для решения задач

- вычисляет площадь трапеции

Этап урока/ время

действия педагога

действия ученика

оценивание

ресурсы

Начало урока( 7 минут)

Организационный момент

Создание коллаборативной среды. Игра - «Зеркало»

Сообщение темы и цели урока. Метод «Дерево ожиданий»

Актуализация знаний учащихся:

«Мозговой штурм» Актуализация имеющихся занний учащихся

Задание 1. 

1.Что такое трапеция: определение и виды

2.Как называются стороны трапеции?

3. Сформулируйте и запишите формулу вычисления средней линии трапеции

5. Что называют высотой трапеции?

6. Запишите два  примера разного вида работ, где  необходимо вычислять площадь трапеции

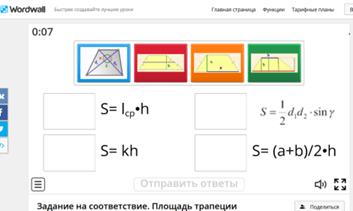
Задание 2.

Задание на соответствие. Найдите  соответствия между картинкой и формулой. (ссылка на wordwall.net )

Форма работы: индивидуальная

Критерии оценивания:

- записывает формулу площади трапеции

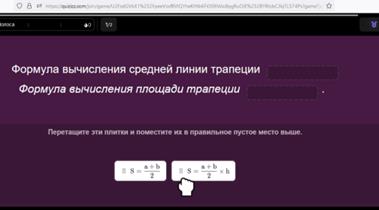
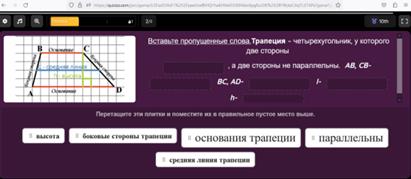
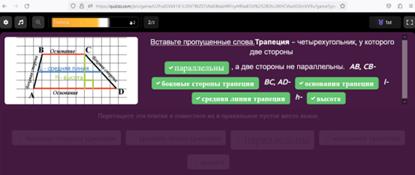
 Поддержка детей с  ООП:

Форма работы: индивидуальная

Прием «Вставь пропущенные слова». Актуализация имеющиеся знания.

Учащийся заполняет пропуски  на платформе quizizz.com ( ссылка на quizizz.com)

Критерии оценивания:

- записывает формулу площади трапеции

Учащиеся  в парах воспроизводят действия или  мимику друг друга, принимая роль зеркала и смотрящего в зеркало, после увеличивая темп.

Свободное обсуждение  мнений участников

Отвечают устно и письменно на вопросы учителя

1. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Виды: произвольная, равнобокая и прямоугольная

2. Параллельные стороны являются основаниями, а непараллельные – боковыми сторонами.

3. Средней линией трапеции называют отрезок, который соединяет середины боковых сторон.
4. Средняя линия трапеции параллельна основаниям и равна половине их суммы.

5. Высота трапеции-это перпендикуляр, опущенный с любой точки прямой, которая содержит одну из основ на прямую, которая содержит другую основу.

8. Покрыть крышу, сшить юбку, покрасить стол, пол и так далее.

Словестная похвала учителя

Устная обратная связь

самопроверка

Стикеры зеленого и оранжевого цвета , маркеры,  рисунок «Дерево ожиданий»

ИКТ

Задание на соответствие. Площадь трапеции - Сопоставить (wordwall.net)

ИКТ

https://quizizz.com/admin/quiz/64a3d3af0c7d67001ddc39e3?source=quiz_share

Середина урока( 33 минут)

Учащимся предлагается карточка с дифференциацией задач по уровню сложности.

Используется прием «Большой палец вверх- вниз».

Для поддержки детей с ООП,  предложена пара с более сильным учащимся

Уровень 1( выполняют все учащиеся )

а) Основания трапеции 5 и 7 см, найдите среднюю линию.

Поддержка ученика  с ООП:

б) Средняя линия трапеции 4,5 см, одно основание 3,2 см, сколько см второе основание?

Поддержка ученика  с ООП:  a= 2· l -b

в) Основания трапеции 11 см и 17 см, а высота 8 см. Вычислите площадь данной трапеции

Поддержка ученика с  ООП:

Уровень 2 ( выполняют многие учащиеся)

Основания трапеции 0,65 см и 0,95 см, площадь 0,56 см². Найдите высоту трапеции.

Поддержка детей с ООП: (a=0,65 см  b= 0,95   S= 0.56 см   h= ), вычисляет, используя калькулятор

Уровень 3 (выполняют некоторые учащиеся)

В равнобедренной трапеции меньшее основание и боковые стороны равны. Основания 5 см и 13 см. Вычислите площадь равнобедренной трапеции.

Поддержка детей с ООП: (h=3 см)

Для ученика ООП подготовлен дополнительно чертеж, и дана высота.

Физкульминутка

«Геометричекая зарядка»

Учащиеся закрывают глаза, представляют яркую точку. От точки проводят отрезок. От отрезка проводят трапецию. В трапеции проводят высоту. Проводят среднюю линию трапеции. Проводят диагонали и тд…

Результатом является уменьшение времени решения задач, за счет представления учащимися рисунка в нужном ракурсе и почти в готовом решении. Способствует развитию образного или пространственного мышления. Что играет немаловажную роль при решении задач на уроках геометрии.

Групповая работа

Прием «Два, четыре – вместе»                                             

Комплексное задание «Закупка окон» (2 задания).

Прочитайте текст и выполните задания 1-2.

Закупка окон

Компания «Дом для семьи» занимается строительством коттеджных посёлков. Для остекления коттеджей она закупает у фирмы по изготовлению окон различные виды окон.

Образцы окон с размерами в миллиметрах представлены на рисунках.

трапециевидное   а)                 трапециевидное    б)           прямоугольное

Цены одного квадратного метра различных видов окон представлены в таблице ниже.

1. Отметьте «Верно» или «Неверно» для каждого утверждения в таблице, приведённой ниже.

Поддержка ученика  с ООП:

Пошаговая инструкция:

1.Из таблицы вычисли разность цен прямоугольного и трапециевидного б) окон. Отметь галочкой ответ на вопрос справа

2.Вычисли площадь трапециевидного б) окна:

S= ( где a=1,5м, b= 2 м, h= 1,5 м )

3.Вычисли площадь прямоугольного окна, применив формулу S=a·b ( где  a=1,3 м·b=1,4 м)

4.Вычисли разность полученных площадей и отметь справа галочкой ответ

2. Фирма по изготовлению окон предоставляет покупателям следующие скидки:

Какую сумму за покупку 30 трапециевидных ( б) ) окон заплатит строительная компания фирме с учётом скидок?

Поддержка ученика  с ООП:

Пошаговая инструкция и поддержка более сильного ученика

1.      Вычисли площадь трапециевидного а) окна, если площадь одного окна S= ( где a=1,5м, b= 2 м, h= 1,5 м )

2.      Вычисли площадь 30 окон трапециевидной формы, используя выражение  выражение 30· S

3.      Вычисли стоимость 30 окон трапециевидной формы, используя выражение  выражение 30· S ·30 000 тг

4.      Определи скидку при заказе товара на полученную сумму

5.      Вырази проценты в виде десятичной дроби, разделив на 100 %

6.      Рассчитай чему равна сумма скидки

7.      Вычисли разность пункта 3 и пункта 6. Запиши ответ задачи

Ответ:                                 тг

Решение: __________________________________________________________________

Учитель во время работы учащихся наблюдает, помогает при необходимости.

При необходимости учитель оказывает консультативную помощь учащимся, направляя их на верный ход решения.

Ответ: 6 см

l=

Ответ:

а=2·l-b

а=4,5

Ответ:84 см²

S=см²

Работа в парах

Ответ: 0,7 см

h=

h=

Ответ: 27 см²

Решение:

AB=CD=5см

ВС=5 см

Проведем перпендикуляр ВL и CM из вершин В и C

LM= ВС=5 см

Рассмотрим ∆ ABL и  ∆DCM

1.      AB=CD( по условию)

2.      ВL=CM(BC ll AD)

∆ ABL =  ∆DCM

 ( по катету и гипотенузе)

AL=MD=(13-5)/2=4
∆АВL ВL²=25-16=9
ВМ=3
S=·3=9·3=27см²

индивидуально

 Учащиеся выполняют работу самостоятельно, затем обговаривают в парах, далее объединяются в четверки, где выполняют оформление решения на постерах. Всем классом идет выбор последовательного и подробного верного решения.

Ответ:

1. 28500-17300=11200  (неверно)

2.S тр. а) =2,625 м²

S пр-ка= 1,82 м²

S тр- S пр-ка= 2,625-1,82 = 0,805 м² ( верно)

Ответ:

1)S тр. б) =м²

2) S пр-ка=0,6·1,2= 0,72 м²

3) S тр. б)+ S пр-ка=0,72+0,57=1,29 м² – площадь 1 окна

4) 1,29·30·28500=11029500 (тг)

3) 1102950-10%= 1102950-110295= 992655 (тг)

Учащиеся решают задания индивидуально на местах задания первого уровня, затем второго- в парах .Для более сильных учащихся предлагаются задания третьего уровня- индивидуально. Выполняется проверка по модельному ответу

Обратная  связь с помощью приема «Большой палец» вверх-вниз

Дескриптор обучающийся:

- вычисляет среднюю линию трапеции, применяя формулу( 1б)

Дескриптор обучающийся:

-  вычисляет основание, применяя формулу средней линии трапеции ( 1б)

Дескрипторы: обучающийся

 - применяет формулу площади трапеции для решения задач( 1б)

- вычисляет площадь трапеции ( 1б)

Выполняется взаимооценивание

по модельному ответу

Дескрипторы: обучающийся:

-выполняет чертеж к задаче

- применяет формулу площади трапеции для решения задач; ( 1б)

- вычисляет высоту( 1б)

 - записывает ответ( 1б)

Дескрипторы: обучающийся:

- определяет длину меньшего основания ( 1б)

- применяет признаки равенства прямоугольных треугольников ( 1б)

- вычисляет высоту трапеции ( 1б)

-применяет формулу площади трапеции для решения задач ( 1б)

- вычисляет площадь трапеции ( 1б)

Наблюдение и похвала учителем

В групповой работе учащимся дается задание распределить обязанности в группе

Дескриптор       обучающийся:

- сравнивает  стоимость квадратного метра двух видов окон;(1б)

- записывает формулу площади трапеции; (1б)

- применяет формулу площади трапеции для решения задач; (1б)

- вычисляет площадь окна трапециевидной формы; (1б)

- вычисляет площадь окна прямоугольной формы; (1б)

- вычисляет разность площадей двух видов окон; (1б)

- отмечает верный ответ; (1б)

Дескриптор     обучающийся:

- записывает формулу площади трапеции; (1б)

 -применяет формулу площади трапеции для решения задач (1б)

- вычисляет площадь окна (3б)

- находит стоимость 30 окон;(3б)

- определяет скидку на товар;(1б)

- вычисляет  сумму за покупку 30 окон, с учетом скидки (1б)

- записывает ответ по условию задачи.(1б)

Ресурс взят с сайта

https://smk.edu.kz/Course/Topic/16/7295

Карточка с заданием, тетрадь

А4, маркеры

Слайд

Конец урока (минут)

Рефлексия. Прием «Дерево ожиданий»

 Дифференцированное домашнее задание:

1 задание ( выбери 1 задачу для решения)

Уровень 1. Высота трапеции равно 200 см². Одно основание равно 26 см, высота равна 10 см. Найдите второе основание трапеции.

Уровень 2. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Уровень 3. Чему равно площадь трапеции ABCD (рис 22.8), если площадь закрашенного треугольника равна 3 см²?

2 задание.  Повтори стр 101-102 «Площадь трапеции»

Записывают домашнее задание, выбирают задачу самостоятельно 1 из 3

На этапе рефлексии учащиеся возвращаются к «Дереву ожиданий», для того чтобы подтвердить свои ожидания (опасения) или опровергнуть их

Стикеры зеленого и оранжевого цвета, маркеры

Учебник геометрия 8кл

 Е.А Туяков, В.А. Смирнов, Алматы 2018